62. 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?

输入:m = 3, n = 7
输出:28
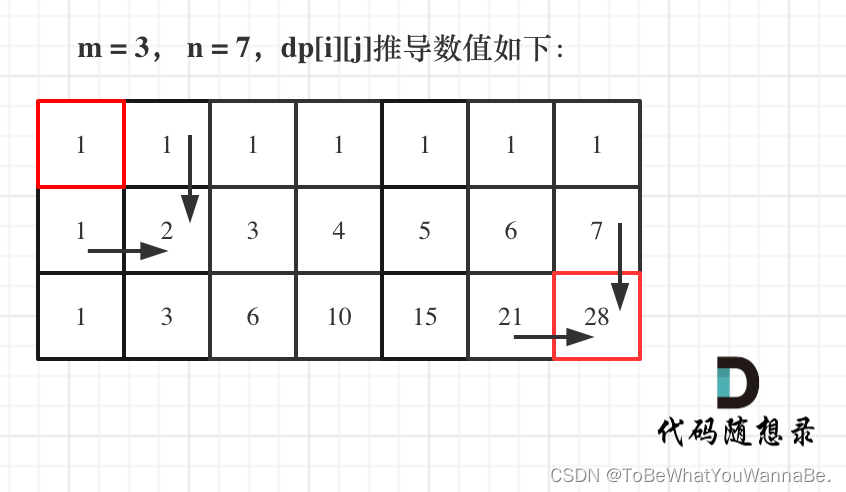
方法一:
/**
* 1. 确定dp数组下标含义 dp[i][j] 到每一个坐标可能的路径种类
* 2. 递推公式 dp[i][j] = dp[i-1][j] dp[i][j-1]
* 3. 初始化 dp[i][0]=1 dp[0][i]=1 初始化横竖就可
* 4. 遍历顺序 一行一行遍历
* 5. 推导结果 。。。。。。。。
*
* @param m
* @param n
* @return
*/
public static int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
//初始化
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (int i = 0; i < n; i++) {
dp[0][i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
这段代码是使用Java实现解决“机器人行走的路径数目”问题,即在一个m x n的网格中,从左上角(0,0)到右下角(m-1,n-1)有多少种行走路径,每次只能向右或向下移动。该问题可以用动态规划(Dynamic Programming, DP)来解决。
代码解析
-
确定dp数组下标含义:
dp[i][j]表示到达网格中坐标为(i, j)位置的不同路径数目。 -
递推公式:到达
(i, j)位置的路径数等于从(i-1, j)位置过来的路径数加上从(i, j-1)位置过来的路径数,即dp[i][j] = dp[i-1][j] + dp[i][j-1]。这是因为机器人到达(i, j)只能是从(i-1, j)向右走一步或从(i, j-1)向下走一步。 -
初始化:边界条件是网格的第一行和第一列,因为从这些边缘出发到它们自身的路径只有一条,即
dp[i][0]=1(第一列)和dp[0][i]=1(第一行)。 -
遍历顺序:按照从上到下、从左到右的顺序遍历网格,先处理好边界和第一行第一列后,逐行逐列计算内部点的路径数目。
-
推导结果:最终,
dp[m-1][n-1]即为到达右下角的路径总数。
示例
假设m=3,n=3,即一个3x3的网格,按照上述代码执行,dp数组会逐步填充如下:
初始状态(考虑初始化):
1 1 1
1 1 1
1 1 1
迭代填充后(忽略边界,根据递推公式):
1 2 3
1 3 6
1 4 10
最终,dp[2][2] = 10,表示从左上角到右下角有10种不同的行走路径。
通过这个动态规划方法,我们可以高效地解决这类路径计数问题。
方法二:
class Solution {
public int uniquePaths(int m, int n) {
// 在二维dp数组中,当前值的计算只依赖正上方和正左方,因此可以压缩成一维数组。
int[] dp = new int[n];
// 初始化,第一行只能从正左方跳过来,所以只有一条路径。
Arrays.fill(dp, 1);
for (int i = 1; i < m; i ++) {
// 第一列也只有一条路,不用迭代,所以从第二列开始
for (int j = 1; j < n; j ++) {
dp[j] += dp[j - 1]; // dp[j] = dp[j] (正上方)+ dp[j - 1] (正左方)
}
}
return dp[n - 1];
}
}
这段Java代码是解决“机器人行走的路径数目”问题的另一种实现,采用了一维动态规划数组来减少空间复杂度。给定一个m x n的网格,从左上角(0,0)到右下角(m-1,n-1)有多少种行走路径,每次只能向右或向下移动。下面是代码的详细解析:
代码解析
-
初始化一维dp数组:由于计算某个位置的路径数只与其正上方和正左方的路径数有关,因此可以使用一维数组
dp来存储到达每列底部的路径总数。数组长度为n,初始化时考虑到第一行的每个位置都只有1条路径(即自己到自己),所以使用Arrays.fill(dp, 1);初始化。 -
双层循环遍历:外层循环遍历网格的行(从1开始,因为第一行已经初始化),内层循环遍历网格的列(从1开始,因为第一列在初始化时已设定为1)。
-
状态转移方程:对于
dp[j],即到达第i行第j列的路径数,可以通过累加左边一格的路径数dp[j - 1]得到,即dp[j] += dp[j - 1];。这样做是因为到达(i, j)的路径可以看作是从(i - 1, j)向下走一条路径加上从(i, j - 1)向右走一条路径的所有组合。 -
返回结果:遍历完成后,
dp[n - 1]存储了到达右下角的路径总数,直接返回这个值即可。
优势
- 空间优化:相比于二维数组的解法,这里只使用了一维数组来存储每行的结果,从而将空间复杂度从O(mn)降低到了O(n),对于大规模的m和n来说,这是一个显著的优势。
- 计算逻辑简洁:通过巧妙地复用一维数组,避免了额外的空间开销,同时也保持了逻辑的直观性。
示例
假设m=3,n=3,执行上述代码后,dp数组会经历以下变化:
- 初始化后:
dp = [1, 1, 1] - 第一轮外层循环后:
dp = [1, 2, 3](到达第二行各列的路径数) - 第二轮外层循环后:
dp = [1, 3, 6](到达第三行各列的路径数,最终结果)
最终返回dp[n - 1] = 6,表示从左上角到右下角有6种不同的行走路径。
63. 不同路径 II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
- 向右 -> 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右 -> 向右

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
方法一:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
//如果在起点或终点出现了障碍,直接返回0
if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {
return 0;
}
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
dp[0][j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;
}
}
return dp[m - 1][n - 1];
}
}
这段Java代码是用于解决“有障碍的格子”的独特路径问题。给定一个二维数组obstacleGrid,其中0表示可以通过的格子,1表示障碍物。你要从左上角(0,0)移动到右下角(m-1, n-1),每次只能向右或向下移动。该函数计算并返回从起点到终点的不同路径数目,如果无法到达终点则返回0。
代码解析:
-
初始化变量:首先获取网格的行数
m和列数n,并创建一个与obstacleGrid同样大小的二维数组dp来存储到达每个格子的路径数。 -
检查起点和终点:如果终点或起点有障碍物,直接返回0,因为这意味着没有路径可达。
-
初始化边界条件:遍历第一列和第一行,如果格子不是障碍物,将其路径数设为1。这表示从起点开始向右或向下有一条路径。
- 对于第一列:
dp[i][0] = 1(若无障碍) - 对于第一行:
dp[0][j] = 1(若无障碍)
- 对于第一列:
-
动态规划填充dp数组:从第二行和第二列开始,对于每个格子
(i, j),如果该格子不是障碍物,则其路径数为上面格子(i-1, j)的路径数加上左边格子(i, j-1)的路径数,即dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。如果遇到障碍物,则该位置的路径数设为0,因为不能通过。 -
返回结果:最后,
dp[m - 1][n - 1]存储了到达终点的路径数目,返回该值作为结果。
示例
假设obstacleGrid为:
[
[0, 0, 0],
[0, 1, 0],
[0, 0, 0]
]
运行这段代码会返回2,因为从左上角到右下角只有两条路径可走,且中间的障碍物阻止了其他可能的路径。
方法二:
// 空间优化版本
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[] dp = new int[n];
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
dp[j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 0; j < n; j++) {
if (obstacleGrid[i][j] == 1) {
dp[j] = 0;
} else if (j != 0) {
dp[j] += dp[j - 1];
}
}
}
return dp[n - 1];
}
}
这段代码是针对“有障碍的格子”的独特路径问题的空间优化版本。与之前的解决方案相比,这里使用了一维数组dp来代替二维数组,从而节省了空间。代码依然计算从二维数组obstacleGrid的左上角到右下角的无障碍路径数量,其中1表示障碍物,0表示可通过的路径。
代码解析
-
初始化变量:获取网格的行数
m和列数n,并声明一个一维数组dp,长度为n,用于记录到达当前列的路径数。 -
初始化第一行:遍历第一行的列,只要遇到无障碍物(
obstacleGrid[0][j] == 0),就将dp[j]设为1,表示从起点到这一列有一条路径。 -
动态规划填充dp数组:
- 遍历每一行(从第二行开始),对于每一行中的每一列:
- 如果当前格子是障碍物,那么到达该格子的路径数为0,因此
dp[j] = 0。 - 如果当前格子不是障碍物,有两种情况:
- 如果是第一列(
j == 0),则只能从上方到达,因此dp[j] = dp[j](保持不变,实际上这种情况在循环外已处理,此处默认处理下一列的情况)。 - 如果不是第一列,到达当前格子的路径数等于上方格子的路径数加上左侧格子的路径数(因为只能向上或向左移动),即
dp[j] += dp[j - 1]。
- 如果是第一列(
- 如果当前格子是障碍物,那么到达该格子的路径数为0,因此
- 遍历每一行(从第二行开始),对于每一行中的每一列:
-
返回结果:最后返回
dp[n - 1],即到达终点的路径数量。
优点
- 空间优化:相比使用二维数组的解法,这里仅使用一维数组存储每行的路径数,将空间复杂度从O(mn)降低到O(n),在处理大尺寸矩阵时更加高效。
示例
假设obstacleGrid为:
[
[0, 0, 0],
[0, 1, 0],
[0, 0, 0]
]
该代码会返回2,表示有两条路径可以从左上角走到右下角,且避开了中间的障碍物。