【机器学习-10】 | Scikit-Learn工具包进阶指南：Scikit-Learn工具包之支持向量机模块研究

🎩 欢迎来到技术探索的奇幻世界👨‍💻

📜 个人主页：@一伦明悦-CSDN博客

✍🏻 作者简介： C++软件开发、Python机器学习爱好者

🗣️ 互动与支持：💬评论 👍🏻点赞 📂收藏 👀关注+

如果文章有所帮助，欢迎留下您宝贵的评论，

点赞加收藏支持我，点击关注，一起进步！

前言

支持向量机（Support Vector Machine, SVM）是一种强大且灵活的监督学习算法，用于分类和回归分析。它特别适用于小样本数据集上的分类问题，同时也能有效地处理高维空间数据。以下是支持向量机的详细分析和解释：

原理和工作方式：

基本概念：

SVM 的基本目标是找到一个超平面（在二维空间中即为一条直线，在更高维空间中为一个超平面），能够将不同类别的数据点尽可能分开，同时具有最大的间隔（margin）。

间隔和支持向量：

间隔是指超平面与离它最近的训练样本点之间的距离。支持向量则是离超平面最近的那些点。在优化过程中，SVM 将寻找最大化间隔的超平面，并且只有支持向量对超平面的位置起决定性作用。

数学形式：

SVM 的数学形式可以用凸优化理论来描述，主要包括最小化正则化的损失函数和约束条件。常见的损失函数包括 Hinge Loss，正则化项可以是 L1 或 L2 范数。

主要优点：

高效处理高维空间数据：由于其核函数技巧，SVM 在高维空间中处理数据效果显著。
泛化能力强：在小样本数据上表现良好，并且能够有效避免过拟合。
可以解决非线性问题：通过选择合适的核函数（如多项式核、高斯核等），SVM 可以处理非线性分类问题。

主要缺点：

计算效率低下：对于大规模数据集和特征数量较多的情况，训练时间较长且消耗资源。
对参数调节和核函数的选择敏感：选择不当可能导致性能下降。

应用领域：

文本分类：如情感分析、垃圾邮件过滤等。
图像分类：例如人脸识别、物体识别等。
生物信息学：如蛋白质分类、基因分类等。

SVM 的工作流程：

数据准备：选择合适的特征和标签。
选择核函数：根据问题选择合适的核函数或者直接使用线性核。
训练模型：通过优化算法找到最优的超平面。
预测：使用训练好的模型对新数据进行分类或回归预测。

正文

01-使用带有RBF核的非线性SVC执行二分类任务

        使用带有RBF核的非线性支持向量机（SVM）执行二分类任务是一种常见且强大的方法。RBF核（径向基函数核）允许SVM处理非线性可分的数据集，通过将数据映射到高维空间来构建一个非线性的决策边界。

1. RBF核的基本概念

RBF核是SVM中最常用的核函数之一，其数学形式为：

$[ K(\mathbf{x}_i, \mathbf{x}_j) = \exp \left( -\gamma |\mathbf{x}_i - \mathbf{x}_j|^2 \right) ]$

其中， $( \gamma )$ 是一个控制RBF核函数衰减速度的参数，( $\mathbf{x}_i$ ) 和 ( $\mathbf{x}_j$ ) 是数据点。

2. 非线性SVM的工作原理

特征映射：RBF核通过将输入数据映射到一个高维特征空间，使得原始的非线性可分问题在这个空间中变得线性可分或更容易分割。

最大化间隔：与线性SVM类似，非线性SVM也寻求一个最大化间隔的超平面来分割不同类别的数据点。这个超平面在高维特征空间中对应于一个非线性的决策边界。

支持向量：在优化过程中，只有位于间隔边界上的支持向量对构建决策边界起作用。它们决定了最终模型的形状和位置。

3. 实施步骤

数据准备

        首先，准备包含特征和标签的训练数据集。

选择核函数

        针对非线性问题，选择RBF核函数是常见且有效的选择。通过调节 ( \gamma ) 参数可以控制决策边界的复杂度，过高或过低的 ( \gamma ) 值都可能导致性能下降。

训练模型

        使用训练数据集训练非线性SVM模型。训练过程包括优化SVM的损失函数和间隔最大化的目标。

模型预测

        使用训练好的模型对新的数据进行分类预测。模型将根据学习到的决策边界将新数据点分配给各个类别。

4. 优缺点

优点：能够有效处理非线性问题，具有良好的泛化能力，适用于各种复杂的数据分布。
缺点：依然对参数 ( \gamma ) 和 ( C ) （正则化参数）敏感，需要仔细调参以达到最佳性能。

5. 应用领域

        非线性SVM在各种领域都有广泛的应用，特别是在图像识别、文本分类、生物信息学等需要处理复杂数据结构的任务中表现出色。

        通过以上步骤和理解，可以详细分析和解释使用带有RBF核的非线性SVM执行二分类任务的过程及其在实际应用中的意义和影响。

这段代码演示了如何使用支持向量机（SVM）进行二分类，并使用 NuSVC 模型拟合一个 XOR 数据集，并可视化决策边界。

代码解释

数据生成：
```
xx, yy = np.meshgrid(np.linspace(-3, 3, 500),
                     np.linspace(-3, 3, 500))
np.random.seed(0)
X = np.random.randn(300, 2)
Y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)
```
- meshgrid 创建了一个二维网格 xx 和 yy，用于绘制决策边界。
- np.random.randn(300, 2) 生成一个包含300个样本的二维随机数据集 X。
- logical_xor 创建了标签 Y，其为 True 当且仅当 X[:, 0] > 0 与 X[:, 1] > 0 中有一个成立时。
模型拟合：
```
clf = svm.NuSVC(gamma='auto')
clf.fit(X, Y)
```
- 使用 NuSVC 模型初始化一个支持向量机分类器，gamma='auto' 表示自动选择核函数的参数。
- 使用 fit 方法拟合模型到数据集 (X, Y) 上。
决策函数计算：
```
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
```
- decision_function 计算网格上每个点的决策函数值，这些值用于绘制决策边界。
- np.c_[xx.ravel(), yy.ravel()] 将网格点展平并连接成二维数组，以便作为输入进行预测。
- Z 被重塑为与网格 xx 相同的形状，以便用于绘制。

可视化：

plt.imshow(Z, interpolation='nearest',
           extent=(xx.min(), xx.max(), yy.min(), yy.max()), aspect='auto',
           origin='lower', cmap=plt.cm.PuOr_r)
contours = plt.contour(xx, yy, Z, levels=[0], linewidths=2,
                       linestyles='dashed')
plt.scatter(X[:, 0], X[:, 1], s=30, c=Y, cmap=plt.cm.Paired,
            edgecolors='k')
plt.xticks(())
plt.yticks(())
plt.axis([-3, 3, -3, 3])
plt.show()

imshow 显示决策函数 Z 的值作为背景色彩图，extent 确定显示范围，cmap 为颜色映射。
contour 绘制决策边界，使用 levels=[0] 表示绘制决策函数为0的等高线。
scatter 绘制样本数据点 X，根据标签 Y 的不同类别使用不同的颜色。
其他绘图设置用于美化图像和删除坐标轴标签。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm

xx, yy = np.meshgrid(np.linspace(-3, 3, 500),
                     np.linspace(-3, 3, 500))
np.random.seed(0)
X = np.random.randn(300, 2)
Y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)

#（译者注：可以在这里通过显示Y来查看什么是XOR数据）

# 拟合模型
clf = svm.NuSVC(gamma='auto')
clf.fit(X, Y)

# 在网格上为每个数据点绘制决策函数
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.imshow(Z, interpolation='nearest',
           extent=(xx.min(), xx.max(), yy.min(), yy.max()), aspect='auto',
           origin='lower', cmap=plt.cm.PuOr_r)
contours = plt.contour(xx, yy, Z, levels=[0], linewidths=2,
                       linestyles='dashed')
plt.scatter(X[:, 0], X[:, 1], s=30, c=Y, cmap=plt.cm.Paired,
            edgecolors='k')
plt.xticks(())
plt.yticks(())
plt.axis([-3, 3, -3, 3])
plt.savefig("../5.png", dpi=500)
plt.show()

结果如下图所示：

图像显示了使用非线性 SVM（使用 RBF 核）在 XOR 数据集上学习的决策边界。这个数据集在原始空间中是线性不可分的，但在高维特征空间中可能是线性可分的。关键点包括：

背景色彩图：显示了决策函数的值，越接近0的区域表示决策边界附近。
虚线等高线：标记了决策函数为0的等高线，即决策边界。
散点图：显示了原始数据点，根据其标签用不同颜色表示不同类别。

这种图像演示了 SVM 如何利用 RBF 核处理非线性问题，并展示了如何在二维空间中绘制决策边界和样本点。

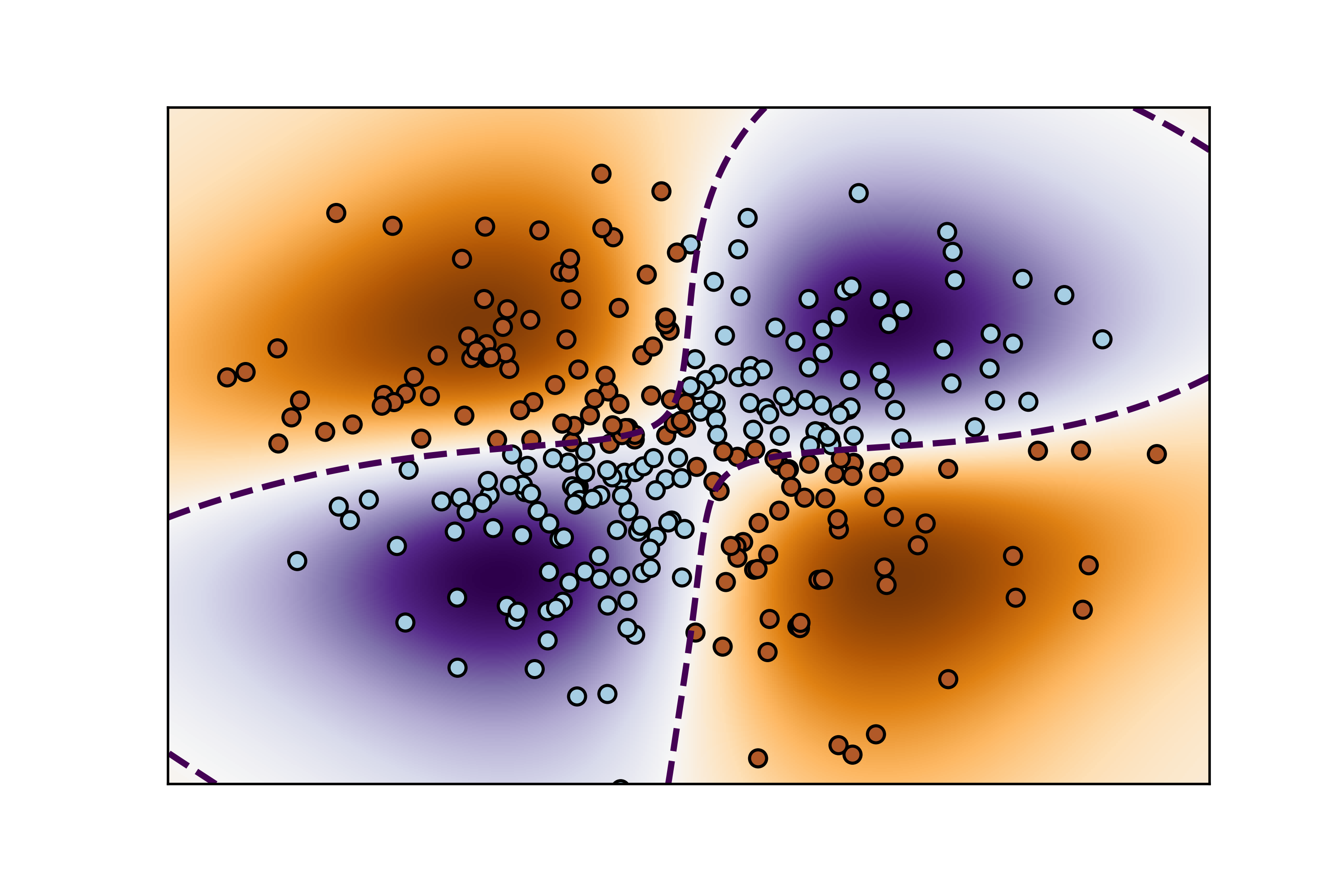
02-支持向量机：最大边际分割超平面

支持向量机（SVM）中的最大边际分割超平面是指通过优化过程找到的能够将不同类别数据点分开并且具有最大间隔（margin）的超平面。以下是对这个概念的详细解释：

基本概念

超平面：

在二维空间中，超平面是一条直线；在更高维空间中，它是一个线性决策边界。超平面能够将特征空间划分为两个部分，每个部分包含一个类别的数据点。

间隔（Margin）：

间隔是指超平面与离它最近的训练样本点之间的距离。在 SVM 中，优化的目标是找到最大化间隔的超平面，这使得模型对未见过的数据具有更好的泛化能力。

支持向量（Support Vectors）：

支持向量是离超平面最近的那些数据点。它们是在优化问题中决定超平面位置和方向的关键元素。支持向量的位置对于定义决策边界和最大化间隔至关重要。

工作原理

SVM 的优化过程旨在找到一个超平面，使得：

所有的正样本点（属于一个类别的数据点）距离超平面的距离大于等于一个正常数，表示为 ( \gamma )；
所有的负样本点（属于另一个类别的数据点）距离超平面的距离小于等于一个负常数，表示为 -( \gamma )。

这可以表达为以下约束条件：
[ y_i (\mathbf{w} \cdot \mathbf{x}_i + b) \geq \gamma \quad \text{对于正样本} ]
[ y_i (\mathbf{w} \cdot \mathbf{x}_i + b) \leq -\gamma \quad \text{对于负样本} ]

其中，( \mathbf{w} ) 是超平面的法向量，( b ) 是偏置项，( y_i ) 是样本 ( \mathbf{x}_i ) 的类别标签。

数学形式

SVM 的目标函数可以形式化为一个凸优化问题，通常包括：

最小化损失函数（如 Hinge Loss）和/或
正则化项（如 ( L1 ) 或 ( L2 ) 范数）

这些组成部分一起用来确保找到一个最大边际的超平面，并在优化过程中保持其对训练数据的泛化能力。

总结

最大边际分割超平面是支持向量机中核心的概念之一，它通过最大化类别之间的间隔来优化模型的泛化能力。这种方法使得 SVM 在处理小样本数据和高维特征空间中表现出色，但也需要仔细调参和处理核函数选择等问题，以达到最佳性能。

这段代码演示了如何使用支持向量机（SVM）进行二分类，并在二维空间中绘制决策边界、支持向量以及间隔。让我们逐步解释和分析代码：

代码解释

生成数据集：
```
X, y = make_blobs(n_samples=40, centers=2, random_state=6)
```
- 使用 make_blobs 生成一个包含40个样本的二维数据集 X，每个样本属于两个中心之一，由 centers=2 指定，random_state 用于复现结果。
模型拟合：
```
clf = svm.SVC(kernel='linear', C=1000)
clf.fit(X, y)
```
- 使用 SVC 初始化一个线性核的支持向量机分类器，C=1000 表示正则化参数的倒数，控制间隔的硬度。
- 使用 fit 方法将模型拟合到数据集 (X, y) 上。
绘制数据点：
```
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)
```
- 使用 scatter 绘制数据点 X，不同的类别用不同的颜色标识，颜色映射为 Paired。
绘制决策函数结果：
```
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)

ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])
```
- 获取当前图形对象 ax 并获取当前的 x 和 y 轴限制。
- 创建一个网格 xx 和 yy，并用 meshgrid 将它们组合成 XX, YY。
- decision_function 计算网格上每个点的决策函数值，并将结果绘制为等高线 contour。
- levels=[-1, 0, 1] 表示绘制决策函数为 -1, 0, 1 的等高线，分别对应于间隔的边界和决策边界。
绘制支持向量：
```
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
           linewidth=1, facecolors='none', edgecolors='k')
```
- 使用 scatter 绘制支持向量，这些向量是决策边界上最靠近数据点的样本。
- clf.support_vectors_ 包含支持向量的坐标，s=100 控制支持向量的大小，facecolors='none' 表示使用空心圆点，edgecolors='k' 表示边框颜色为黑色。
保存和显示图像：
```
plt.savefig("../5.png", dpi=500)
plt.show()
```
- 使用 savefig 保存图像为 5.png，分辨率为 500 dpi。
- plt.show() 显示生成的图像。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs


# 我们创建40个用来分割的数据点
X, y = make_blobs(n_samples=40, centers=2, random_state=6)

# 拟合模型，并且为了展示作用，并不进行标准化
clf = svm.SVC(kernel='linear', C=1000)
clf.fit(X, y)

plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)

# 绘制decision function的结果
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

# 创造网格来评估模型
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)

# 绘制决策边界和边际
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])
# 绘制支持向量
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
           linewidth=1, facecolors='none', edgecolors='k')
plt.savefig("../5.png", dpi=500)
plt.show()

这幅图展示了线性核支持向量机在二维空间中的工作效果：

散点图：显示了生成的二维数据集，每个类别用不同颜色表示。
等高线：展示了决策函数的值，黑色虚线表示决策边界，而实线则表示间隔的边界。
支持向量：用大圆圈表示的支持向量，它们是决策边界上距离最近的数据点。

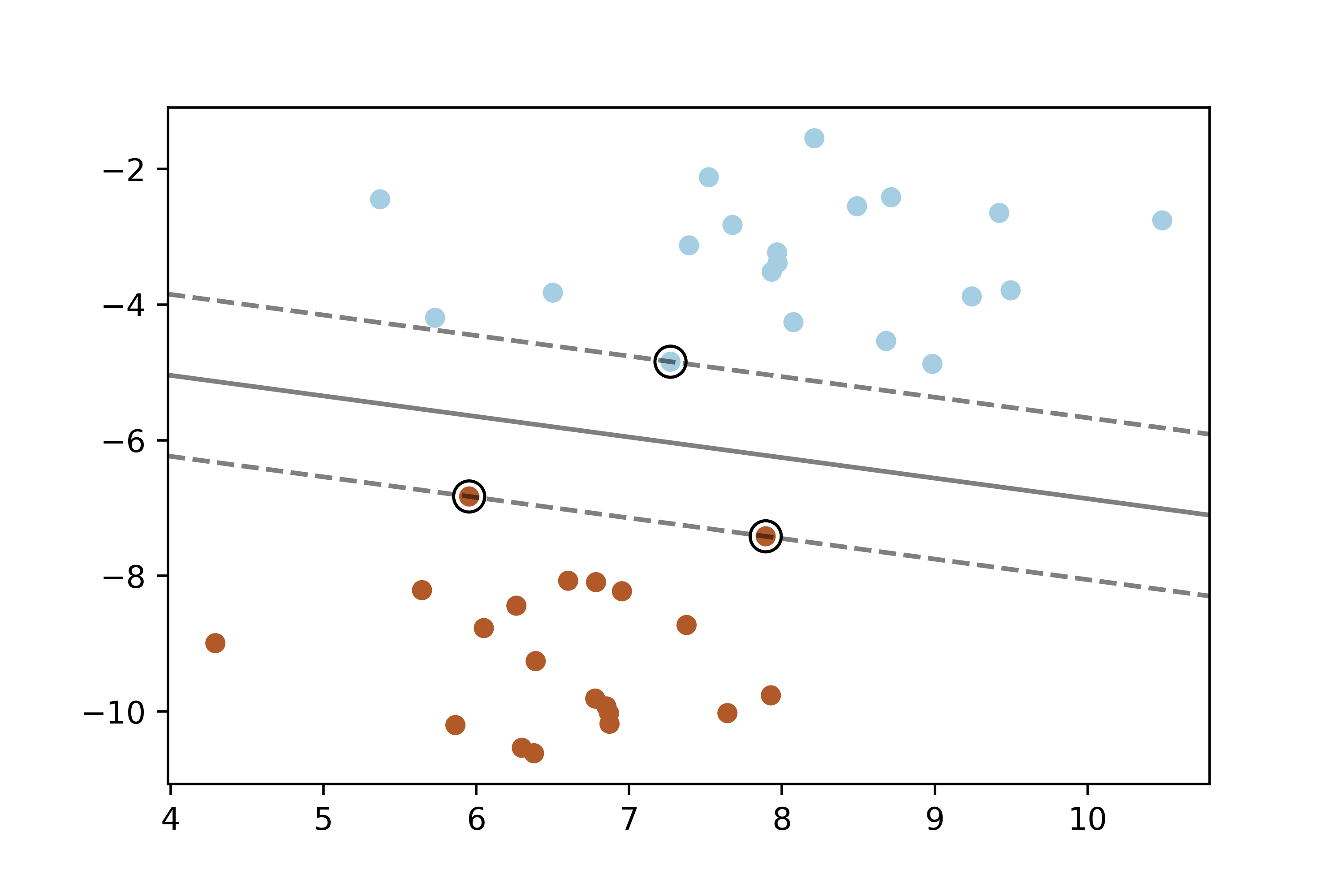
03-带有自定义核函数的支持向量机

带有自定义核函数的支持向量机（SVM）允许在非线性可分的情况下进行分类，通过将数据映射到高维特征空间来实现线性分离。以下是对带有自定义核函数的SVM的详细解释：

基本概念

核函数：

核函数是SVM中的关键概念，它定义了数据如何从输入空间映射到特征空间。在线性不可分的情况下，通过核函数可以在高维空间中找到线性分割超平面，而无需显式计算高维特征空间的数据表示。

支持向量机：

SVM是一种监督学习算法，其目标是找到一个超平面来最大化不同类别数据点之间的间隔。对于线性不可分的情况，引入核函数使得SVM可以处理复杂的数据结构，如曲线或高度非线性分布的数据。

工作原理

带有自定义核函数的SVM的工作原理如下：

核方法：

SVM使用核方法计算数据点之间的相似性，而不是直接操作高维空间中的数据。核函数可以是多种类型，如线性、多项式、高斯（径向基函数）等。

非线性映射：

核函数将输入空间中的数据映射到高维特征空间，使得在高维空间中可能是线性可分的。例如，径向基函数（RBF）核会将数据映射到无限维的特征空间，在此空间中，数据点更有可能是线性可分的。

决策边界：

在高维特征空间中，SVM寻找一个最优超平面来分割数据。这个超平面可以被视为在原始输入空间中复杂边界的映射。

数学形式

使用核函数的SVM的数学形式如下：

给定一个核函数 ( K(\mathbf{x}_i, \mathbf{x}_j) )，它可以通过内积计算两个数据点 ( \mathbf{x}_i ) 和 ( \mathbf{x}_j ) 在特征空间中的相似度。

优化目标仍然是找到一个超平面 ( \mathbf{w} \cdot \Phi(\mathbf{x}) + b = 0 )，其中 ( \Phi(\mathbf{x}) ) 是特征空间中的映射函数。

实现和应用

在实际应用中，选择合适的核函数非常重要，它直接影响了模型的性能和泛化能力。常见的核函数有：

线性核函数： $( K(\mathbf{x}_i, \mathbf{x}_j) = \mathbf{x}_i \cdot \mathbf{x}_j )$
多项式核函数： $( K(\mathbf{x}_i, \mathbf{x}_j) = (\gamma \mathbf{x}_i \cdot \mathbf{x}_j + r)^d )$ ，其中 ( \gamma )、 ( r ) 和 ( d ) 是参数。
径向基函数（RBF）核： $( K(\mathbf{x}_i, \mathbf{x}_j) = \exp(-\gamma ||\mathbf{x}_i - \mathbf{x}_j||^2) )$ ，其中 ( \gamma ) 是参数。

总结

带有自定义核函数的支持向量机通过核方法将非线性问题映射到高维空间中进行处理，从而实现了在复杂数据结构中的高效分类。选择合适的核函数和调整其参数对于模型的性能和泛化能力至关重要，这需要根据具体问题进行实验和优化。

这段代码演示了如何使用带有自定义核函数的支持向量机（SVM）对鸢尾花数据集进行分类，并绘制分类结果的决策边界。

代码解释

导入库和数据集
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
```
这里导入了需要使用的库，包括NumPy用于数据处理，Matplotlib用于绘图，以及sklearn中的svm和datasets模块。
加载数据
```
iris = datasets.load_iris()
X = iris.data[:, :2]  # 仅使用前两个特征，这里使用了切片操作
Y = iris.target
```
从鸢尾花数据集中加载数据，仅使用前两个特征（萼片长度和宽度），目标变量为类别标签。

定义自定义核函数

def my_kernel(X, Y):
    """
    我们创建一个自定义的核函数:
    
                 (2  0)
    k(X, Y) = X  (    ) Y.T
                 (0  1)
    """
    M = np.array([[2, 0], [0, 1.0]])
    return np.dot(np.dot(X, M), Y.T)

这里定义了一个简单的自定义核函数，它是一个线性核函数的变体，通过矩阵M对输入数据进行线性变换。

创建SVM实例并拟合数据
```
clf = svm.SVC(kernel=my_kernel)
clf.fit(X, Y)
```
使用svm.SVC创建了一个支持向量机实例，指定了自定义核函数my_kernel，并对数据进行拟合。

生成网格并预测

h = .02  # 设置网格中的步长
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])

创建了一个网格来覆盖输入空间的范围，并使用训练好的SVM模型对每个网格点进行分类预测。

绘制决策边界和数据点
```
Z = Z.reshape(xx.shape)
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)

# 绘制训练点
plt.scatter(X[:, 0], X[:, 1], c=Y, cmap=plt.cm.Paired, edgecolors='k')
```
使用pcolormesh绘制网格中每个点的预测结果，使用scatter绘制原始数据点，其中不同颜色表示不同的类别。

图像设置和显示

plt.title('3-Class classification using Support Vector Machine with custom kernel')
plt.axis('tight')
plt.show()

设置标题和坐标轴，然后显示绘制的图像。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets

# 导入数据以便处理
iris = datasets.load_iris()
X = iris.data[:, :2] 
# 我们仅仅使用前两个特征，我们可以通过使用二维数据集来避免复杂的切片
Y = iris.target


def my_kernel(X, Y):
    """
    我们创建一个自定义的核函数:

                 (2  0)
    k(X, Y) = X  (    ) Y.T
                 (0  1)
    """
    M = np.array([[2, 0], [0, 1.0]])
    return np.dot(np.dot(X, M), Y.T)


h = .02  # 设置网格中的步长

# 我们创建一个SVM实例并拟合数据。
clf = svm.SVC(kernel=my_kernel)
clf.fit(X, Y)

# 绘制决策边界。为此，我们将为网格[x_min，x_max] x [y_min，y_max]中的每个点分配颜色。
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])

# 将结果放入颜色图
Z = Z.reshape(xx.shape)
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)

# 绘制训练点
plt.scatter(X[:, 0], X[:, 1], c=Y, cmap=plt.cm.Paired, edgecolors='k')
plt.title('3-Class classification using Support Vector Machine with custom'
          ' kernel')
plt.axis('tight')
plt.savefig("../5.png", dpi=500)
plt.show()

背景色块和决策边界：
- 背景色块通过颜色区分了不同类别的预测区域，每个颜色块表示SVM预测该区域内的所有点属于同一类别。
- 决策边界是分类器在特征空间中的决策界限，分隔不同类别的区域。
数据点：
- 数据点在图中以散点的形式显示，每种类别使用不同的颜色表示，有助于可视化各个类别在特征空间中的分布。

这样，通过自定义核函数，支持向量机能够有效地处理非线性问题，并提供清晰的分类决策边界。

04-绘制线性支持向量机（基于liblinear）的支持向量

绘制线性支持向量机（Linear SVM）基于liblinear的支持向量，需要了解以下几个关键点：

线性支持向量机（Linear SVM）

核心概念：

线性支持向量机是通过一个线性超平面来分割数据空间，使得不同类别的数据点能够尽可能远离超平面，从而构建最优的分类边界。

支持向量：

支持向量是离超平面最近的数据点，它们决定了超平面的位置。在线性情况下，支持向量通常位于分类边界附近，是决策边界的主要构成部分。

绘制支持向量的步骤解释
使用LinearSVC初始化模型：
from sklearn.svm import LinearSVC
model = LinearSVC()
model.fit(X, Y)
LinearSVC是scikit-learn中专门用于线性SVM分类的模型。通过fit方法训练模型，其中X是特征数据，Y是对应的类别标签。
获取支持向量：
support_vectors = model.support_vectors_
support_vectors_属性可以获取模型中找到的支持向量的数据点。
绘制支持向量和决策边界：
plt.scatter(X[:, 0], X[:, 1], c=Y, cmap=plt.cm.Paired, edgecolors='k')
plt.scatter(support_vectors[:, 0], support_vectors[:, 1], s=100, facecolors='none', edgecolors='k')
使用scatter方法绘制所有数据点，其中不同颜色代表不同类别。
使用scatter方法再次绘制支持向量，通常使用圆圈标识，以突出显示它们。
设置图像属性：
plt.title('Support Vectors of Linear SVM (liblinear)')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
添加标题和坐标轴标签，最后使用show方法展示绘制的图像。
图像解释

数据点：

所有数据点通过散点图显示，颜色表示它们的类别。这些点包括训练集中的所有数据。

支持向量：

通过绘制大圆圈（只有边界没有填充）标识出模型确定的支持向量。这些点是模型决策边界最接近的数据点，对模型的决策起到关键作用。

决策边界：

在线性SVM中，决策边界是一个直线，它在特征空间中分隔不同类别的数据点。

通过这种方式，可以清晰地展示线性支持向量机的工作原理及其在数据集上的表现，特别是如何通过支持向量确定最优的分类边界。

这段代码演示了如何使用Scikit-Learn的LinearSVC绘制线性支持向量机（Linear SVM）的决策边界和支持向量。

代码解释

数据生成与初始化模型
```
X, y = make_blobs(n_samples=40, centers=2, random_state=0)
```
- 使用make_blobs生成一个二分类的数据集，共40个样本，用于模拟实际数据。
模型训练与决策边界绘制
```
for i, C in enumerate([1, 100]):
    clf = LinearSVC(C=C, loss="hinge", random_state=42).fit(X, y)
    decision_function = clf.decision_function(X)
    support_vector_indices = np.where((2 * y - 1) * decision_function <= 1)[0]
    support_vectors = X[support_vector_indices]
```
- 对每个参数C（正则化参数）分别训练一个LinearSVC模型。loss="hinge"指定了线性SVM所使用的损失函数。
- decision_function计算决策函数的值，支持向量的索引通过条件(2 * y - 1) * decision_function <= 1确定。
- 支持向量通过这些索引从数据集X中获取。

绘制图像

plt.subplot(1, 2, i + 1)
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50),
                     np.linspace(ylim[0], ylim[1], 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
            linestyles=['--', '-', '--'])
plt.scatter(support_vectors[:, 0], support_vectors[:, 1], s=100,
            linewidth=1, facecolors='none', edgecolors='k')
plt.title("C=" + str(C))

使用subplot在一行两列中创建子图，分别展示不同参数C的结果。
通过scatter方法绘制所有数据点，根据类别用不同颜色标示。
使用contour函数绘制决策边界，其中levels=[-1, 0, 1]绘制了决策函数为-1、0、1的等高线，代表不同的决策边界。
通过scatter绘制支持向量，使用大圆圈表示，以突出显示它们。

图像属性设置与展示
```
plt.tight_layout()
plt.savefig("../5.png", dpi=500)
plt.show()
```
- 使用tight_layout确保图像布局合适。
- savefig保存图像为高分辨率PNG格式。
- show展示生成的图像。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.svm import LinearSVC

X, y = make_blobs(n_samples=40, centers=2, random_state=0)

plt.figure(figsize=(10, 5))
for i, C in enumerate([1, 100]):
    # "hinge"是支持向量机惯例使用的损失函数
    clf = LinearSVC(C=C, loss="hinge", random_state=42).fit(X, y)
    # 通过决策函数获得支持向量
    decision_function = clf.decision_function(X)
    # 我们也可以手动计算决策函数
    # decision_function = np.dot(X, clf.coef_[0]) + clf.intercept_[0]
    support_vector_indices = np.where((2 * y - 1) * decision_function <= 1)[0]
    support_vectors = X[support_vector_indices]

    plt.subplot(1, 2, i + 1)
    plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
    xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50),
                         np.linspace(ylim[0], ylim[1], 50))
    Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
                linestyles=['--', '-', '--'])
    plt.scatter(support_vectors[:, 0], support_vectors[:, 1], s=100,
                linewidth=1, facecolors='none', edgecolors='k')
    plt.title("C=" + str(C))
plt.tight_layout()
plt.savefig("../5.png", dpi=500)
plt.show()