【TOOL】ceres学习笔记(一) —

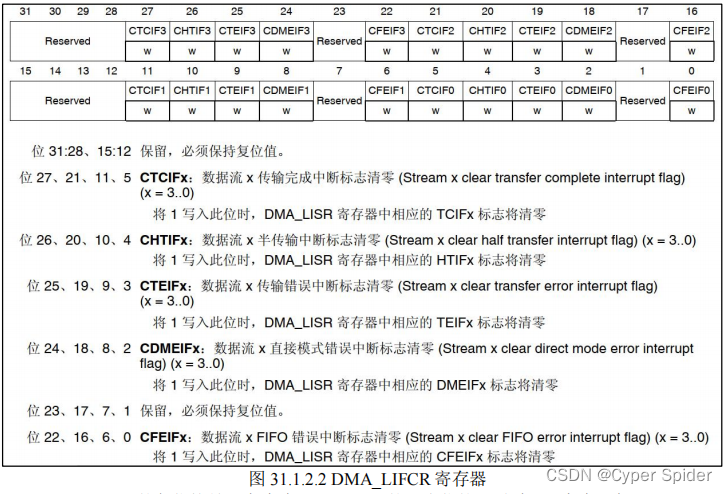
文章目录

一、Ceres Solver 介绍
二、Ceres 使用基本步骤
- 1. 构建最小二乘问题
- 2. 求解最小二乘问题
三、使用案例
- 1. Ceres Helloworld
- 2. Powell’s Function
- 3. Curve Fitting
- 4. Robust Curve Fitting

一、Ceres Solver 介绍

Ceres-solver 是由Google开发的开源C++库，用于解决具有边界约束的非线性最小二乘优化和一般无约束优化问题，成熟、功能丰富、高性能。与一般优化问题不同的是，非线性最小二乘优化问题的目标函数具有明确的物理意义——残差。
具有边界约束的非线性最小二乘鲁棒优化问题形式如下：
$\min _x \frac{1}{2} \sum_i \rho_i\left(\left\|f_i\left(x_{i 1}, \cdots, x_{i k}\right)\right\|^2\right), l_j \leq x_j \leq u_j$

$x_{i1},⋯,x_{ik})$ 在Ceres中被称为参数块（ParameterBlock），通常是几组标量的集合，例如，相机的位姿可以定义成是一组包含3个参数的平移向量（用于描述相机的位置），和包含4个参数的四元数（用于描述相机姿态），当然，参数块也可以只有一个参数， $l_j$ 和 $u_j$ 是参数块中对应每个参数的边界；
$f_i(\cdot)$ 在Ceres中被称为代价函数（CostFuntion），是关于参数块的函数，在一个优化问题中，可能会存在多个代价函数；
$\rho_i(\cdot)$ 在Ceres中被称为损失函数（LossFuntion），是一个标量函数，将代价函数计算出的值映射到另一个区间中的值，用于减少异常值或外点（outliers）对非线性最小二乘优化问题的影响，作用有点类似于机器学习中的激活函数，例如，直线拟合时，对于距离直线非常远的点，应当减少它的权重，损失函数并非是必须的，可以为空（NULL），此时，损失函数值等同于代价函数计算值，即 $\rho_i(t)=t$ ；

当损失函数为空，且参数没有边界时，就是我们熟悉的非线性最小二乘问题，如下：
$\min _x \frac{1}{2} \sum_i \left(\left\|f_i\left(x_{i 1}, \cdots, x_{i k}\right)\right\|^2\right),\qquad l_j =-\infty \quad u_j =\infty$
一般情况下，最小二乘问题与鲁棒最小二乘问题的区别在于鲁棒最小二乘会指定损失函数，具体效果在后续的有关曲线拟合的学习笔记中会有所体现。

$\rho_i\left(\left\|f_i\left(x_{i 1}, \cdots, x_{i k}\right)\right\|^2\right)$ 在Ceres中被称为残差块（ResidualBlock），残差块中包含了参数块、代价函数、损失函数，因此，在添加残差块时，必须指定参数集合、代价函数，视具体情况是否指定损失函数。

统计学中的曲线拟合、计算机视觉中的相机标定、视觉SLAM中的地图生成等问题都可以描述成以上形式。

二、Ceres 使用基本步骤

Ceres 求解过程主要有两大步骤，构建最小二乘问题和求解最小二乘问题，具体步骤如下：

1. 构建最小二乘问题

用户自定义残差计算模型，可能存在多个；
构建Ceres代价函数（CostFuntion），将用户自定义残差计算模型添加至CostFuntion，可能存在多个CostFuntion，为每个CostFuntion添加用户自定义残差计算模型，并指定用户自定义残差计算模型的导数计算方法；
构建Ceres问题（Problem），并在Problem中添加残差块（ResidualBlock），可能存在多个ResidualBlock，为每个ResidualBlock指定CostFuntion，LossFuntion以及参数块（ParameterBlock）；

2. 求解最小二乘问题

配置求解器参数Options，即设置Problem求解方法及参数。例如迭代次数、步长等等；
输出日志内容Summary；
优化求解Solve。

三、使用案例

Ceres 安装 参考之前的 Ubuntu20.04安装VINS_Mono 和 VINS_Fusion 。

1. Ceres Helloworld

以求解如下函数的最小值为例：
$f(x)=\frac{1}{2}(10-x)^2$
对于求解该函数的最小值问题，可以构建成一个非常简单的优化问题，虽然一眼就能看出 x = 10时函数能够获取最小值，但以此为例，可以说明使用 Ceres解决一般优化问题或者非线性最小二乘问题的基本步骤。

1.1 用户自定义残差计算模型

// 用户自定义残差计算模型
struct MyCostFunctorAutoDiff 
{
	// 模板函数
	template<typename Type>
	bool operator()(const Type* const x, Type* residual) const
	{
		// 输入参数x和输出参数residual都只有1维
		residual[0] = 10.0 - x[0];
		return true;
	}
};

注意: operator()是一个模板函数，输入和输出的参数类型都是Type类型，当仅需要获得残差值作为输出时，Ceres在调用MyCostFunctorAutoDiff::operator<Type>()时可以指定Type的类型为double，当需要获得Jacobians值（微分或导数）作为输出时，Ceres在调用MyCostFunctorAutoDiff::operator<Type>()时可以指定Type的类型为Jet。关于operator()仿函数参考 c++仿函数 functor。

1.2 构建Ceres代价函数CostFuntion

// 构建Ceres代价函数CostFuntion，用来计算残差，残差计算方法为用户自定义残差计算模型MyCostFunctorAutoDiff
// 只存在一个代价函数,使用自动微分方法AutoDiffCostFunction来计算导数
// AutoDiffCostFunction<MyCostFunctorAutoDiff, 1, 1>模板参数中，需要依次指定
// 用户自定义残差计算模型MyCostFunctorAutoDiff、输出（resudual）维度大小、输入（参数x）维度大小
// 这两个维度大小需要与残差计算模型中输入、输出参数的维度一致，对应residual[0]和x[0]

ceres::CostFunction* cost_function =
    new ceres:: AutoDiffCostFunction<MyCostFunctorAutoDiff, /* 用户自定义残差计算模型 */\
    1, /* 输出（resudual）维度大小 */\
    1 /* 输入（参数x）维度大小 */>(new MyCostFunctorAutoDiff);

说明：

只存在一个代价函数；
使用自动微分方法来计算导数；
AutoDiffCostFunction<MyCostFunctorAutoDiff, 1, 1>模板参数中，需要依次指定用户自定义残差计算模型MyCostFunctorAutoDiff、输出（resudual）维度大小、输入（参数x）维度大小，这两个维度大小需要与残差计算模型中输入、输出参数的维度一致，对应residual[0]和x[0]；

1.3 构建Ceres问题Problem

// 构建非线性最小二乘问题
ceres::Problem problem;
// 添加残差块，需要依次指定代价函数，损失函数，参数块
// 损失函数为单位函数
problem.AddResidualBlock(cost_function, nullptr, &x);

说明：

添加残差块ResidualBlock时，需要依次指定代价函数CostFunction，损失函数LossFunction（损失函数为单位函数），参数块ParameterBlock;
只添加一项残差块。

1.4 配置求解器参数Options、输出日志内容Summary

// 配置求解器参数
ceres::Solver::Options options;
// 指定线性求解器来求解问题
options.linear_solver_type = ceres::DENSE_QR;
// 输出每次迭代的信息
options.minimizer_progress_to_stdout = true;

// 输出日志内容
ceres::Solver::Summary summary;

1.5 优化求解

// 开始优化求解
ceres::Solve(options, &problem, &summary);

1.6 完整代码

#include "ceres/ceres.h"
#include "glog/logging.h"
#include <iostream>

// 用户自定义残差计算模型
struct MyCostFunctorAutoDiff 
{
   // 模板函数
   template<typename Type>
   bool operator()(const Type* const x, Type* residual) const
   {
   	// 输入参数x和输出参数residual都只有1维
   	residual[0] = 10.0 - x[0];
   	return true;
   }
};

int main(int argc, char** argv)
{
   google::InitGoogleLogging(argv[0]);
   // 设置参数初始值
   const double initial_x = 5;
   double x = initial_x;

   // 构建Ceres代价函数CostFuntion，用来计算残差，残差计算方法为用户自定义残差计算模型MyCostFunctorAutoDiff
   // 只存在一个代价函数,使用自动微分方法AutoDiffCostFunction来计算导数
   // AutoDiffCostFunction<MyCostFunctorAutoDiff, 1, 1>模板参数中，需要依次指定
   // 用户自定义残差计算模型MyCostFunctorAutoDiff、输出（resudual）维度大小、输入（参数x）维度大小
   // 这两个维度大小需要与残差计算模型中输入、输出参数的维度一致，对应residual[0]和x[0]
   ceres::CostFunction* cost_function =
       new ceres:: AutoDiffCostFunction<MyCostFunctorAutoDiff, /* 用户自定义残差计算模型 */\
       1, /* 输出（resudual）维度大小 */\
       1 /* 输入（参数x）维度大小 */>(new MyCostFunctorAutoDiff);

   // 构建非线性最小二乘问题
   ceres::Problem problem;
   // 添加残差块，需要依次指定代价函数，损失函数，参数块
   // 损失函数为单位函数
   problem.AddResidualBlock(cost_function, nullptr, &x);

   // 配置求解器参数
   ceres::Solver::Options options;
   // 指定线性求解器来求解问题
   options.linear_solver_type = ceres::DENSE_QR;
   // 输出每次迭代的信息
   options.minimizer_progress_to_stdout = true;

   // 输出日志内容
   ceres::Solver::Summary summary;
   
   // 开始优化求解
   ceres::Solve(options, &problem, &summary);

   // 输出优化过程及结果
   std::cout << summary.BriefReport() << "\n";
   std::cout << "x : " << initial_x << " -> " << x << "\n";

   std::system("pause");
   return 0;
}

1.7 优化过程及结果
在这里插入图片描述

2. Powell’s Function

$F (x)$ 是一个4参数方程，有4个残差块，希望找到 $x=[x_1,\;x_2,\;x_3,\;x_4]$ 使得 $\frac{1}{2}||F(x)||^2$ 最小。
$\begin{aligned} f_1(x) & =x_1+10 x_2 \\ f_2(x) & =\sqrt{5}\left(x_3-x_4\right) \\ f_3(x) & =\left(x_2-2 x_3\right)^2 \\ f_4(x) & =\sqrt{10}\left(x_1-x_4\right)^2 \\ F(x) & =\left[f_1(x), f_2(x), f_3(x), f_4(x)\right] \end{aligned}$
与上一节 Ceres Helloworld 类似，大部分步骤相同，此处仅分析不同之处。

2.1 构建Ceres问题Problem
首先，以 $f_1(x) =x_1+10 x_2$ 为例，构建 $f_1(x_1,x_2)$ 的自定义残差计算模型：

// 用户自定义残差计算模型
// f1 = x1 + 10 * x2;
struct F1 {
  template <typename T> bool operator()(const T* const x1,
                                        const T* const x2,
                                        T* residual) const {
    residual[0] = x1[0] + 10.0 * x2[0];
    return true;
  }
};

同理，可以定义类 $F 2$ ， $F 3$ 和 $F 4$ 分别去定义 $f_2(x_3,x_4)$ ， $f_3(x_2,x_3)$ 和 $f_4(x_1,x_4)$ 的自定义残差计算模型，这些模型可以构建问题如下：

double x1 =  3.0; double x2 = -1.0; double x3 =  0.0; double x4 = 1.0;

Problem problem;

// Add residual terms to the problem using the autodiff
// wrapper to get the derivatives automatically.
problem.AddResidualBlock(
  new AutoDiffCostFunction<F1, 1, 1, 1>(), nullptr, &x1, &x2);
problem.AddResidualBlock(
  new AutoDiffCostFunction<F2, 1, 1, 1>(), nullptr, &x3, &x4);
problem.AddResidualBlock(
  new AutoDiffCostFunction<F3, 1, 1, 1>(), nullptr, &x2, &x3);
problem.AddResidualBlock(
  new AutoDiffCostFunction<F4, 1, 1, 1>(), nullptr, &x1, &x4);

说明：

存在四个代价函数；
使用自动微分方法来计算导数；
AutoDiffCostFunction<F4, 1, 1, 1> 模板参数中，依次指定用户自定义残差计算模型F4、输出（resudual）维度大小、输入（参数x）维度大小，对应 residual[0] 和 x1[0]，x4[0]。注意，和Ceres Helloworld一节相比，此处每个ResidualBlock依赖两个参数输入(也不是所有四个参数)。；

2.2 完整代码

#include <vector>
#include "ceres/ceres.h"
#include "gflags/gflags.h"
#include "glog/logging.h"

using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;
using ceres::Solve;

struct F1 {
  template <typename T> bool operator()(const T* const x1,
                                        const T* const x2,
                                        T* residual) const {
    // f1 = x1 + 10 * x2;
    residual[0] = x1[0] + 10.0 * x2[0];
    return true;
  }
};

struct F2 {
  template <typename T> bool operator()(const T* const x3,
                                        const T* const x4,
                                        T* residual) const {
    // f2 = sqrt(5) (x3 - x4)
    residual[0] = sqrt(5.0) * (x3[0] - x4[0]);
    return true;
  }
};

struct F3 {
  template <typename T> bool operator()(const T* const x2,
                                        const T* const x3,
                                        T* residual) const {
    // f3 = (x2 - 2 x3)^2
    residual[0] = (x2[0] - 2.0 * x3[0]) * (x2[0] - 2.0 * x3[0]);
    return true;
  }
};

struct F4 {
  template <typename T> bool operator()(const T* const x1,
                                        const T* const x4,
                                        T* residual) const {
    // f4 = sqrt(10) (x1 - x4)^2
    residual[0] = sqrt(10.0) * (x1[0] - x4[0]) * (x1[0] - x4[0]);
    return true;
  }
};

DEFINE_string(minimizer, "trust_region",
              "Minimizer type to use, choices are: line_search & trust_region");

int main(int argc, char** argv) {
  // CERES_GFLAGS_NAMESPACE::ParseCommandLineFlags(&argc, &argv, true);
  gflags::ParseCommandLineFlags(&argc, &argv, true);
  google::InitGoogleLogging(argv[0]);

  double x1 =  3.0;
  double x2 = -1.0;
  double x3 =  0.0;
  double x4 =  1.0;

  Problem problem;
  // Add residual terms to the problem using the using the autodiff
  // wrapper to get the derivatives automatically. The parameters, x1 through
  // x4, are modified in place.
  problem.AddResidualBlock(new AutoDiffCostFunction<F1, 1, 1, 1>(new F1),
                           NULL,
                           &x1, &x2);
  problem.AddResidualBlock(new AutoDiffCostFunction<F2, 1, 1, 1>(new F2),
                           NULL,
                           &x3, &x4);
  problem.AddResidualBlock(new AutoDiffCostFunction<F3, 1, 1, 1>(new F3),
                           NULL,
                           &x2, &x3);
  problem.AddResidualBlock(new AutoDiffCostFunction<F4, 1, 1, 1>(new F4),
                           NULL,
                           &x1, &x4);

  Solver::Options options;
  LOG_IF(FATAL, !ceres::StringToMinimizerType(FLAGS_minimizer,
                                              &options.minimizer_type))
      << "Invalid minimizer: " << FLAGS_minimizer
      << ", valid options are: trust_region and line_search.";

  options.max_num_iterations = 100;
  options.linear_solver_type = ceres::DENSE_QR;
  options.minimizer_progress_to_stdout = true;

  std::cout << "Initial x1 = " << x1
            << ", x2 = " << x2
            << ", x3 = " << x3
            << ", x4 = " << x4
            << "\n";

  // Run the solver!
  Solver::Summary summary;
  Solve(options, &problem, &summary);

  std::cout << summary.FullReport() << "\n";
  std::cout << "Final x1 = " << x1
            << ", x2 = " << x2
            << ", x3 = " << x3
            << ", x4 = " << x4
            << "\n";
  return 0;
}

2.3 优化过程及结果
在这里插入图片描述

3. Curve Fitting

最小二乘和非线性最小二乘分析的最初目的是将曲线拟合到数据中。现在我们来考虑这样一个问题的例子: 数据通过对曲线进行采样生成的数据 $y=e^{0.3x+0.1}$ 并添加具有标准差的高斯噪声 $\sigma=0.2$ 。现在让我们将这些生成的数据拟合到曲线上 $y=e^{mx+c}$ 上。

3.1 构建Ceres问题Problem
首先，定义一个模板对象来评估残差。

struct ExponentialResidual {
  ExponentialResidual(double x, double y)
      : x_(x), y_(y) {}

  template <typename T> 
  bool operator()(const T* const m,
                  const T* const c,
                  T* residual) const {
    residual[0] = y_ - exp(m[0] * x_ + c[0]);
    return true;
  }

 private:
  const double x_;
  const double y_;
};

注意：每个观测值都会有一个残差，假设观测结果2n大小数组称为 data问题构造，只需 CostFunction为每个观察创建一个残差块。

double m = 0.0;
double c = 0.0;

Problem problem;
// version1:
for (int i = 0; i < kNumObservations; ++i) {
  CostFunction* cost_function =
       new AutoDiffCostFunction<ExponentialResidual, 1, 1, 1>
           (data[2 * i], data[2 * i + 1]);
           
  problem.AddResidualBlock(cost_function, nullptr, &m, &c);
}

// version2:
 for (int i = 0; i < kNumObservations; ++i) {
   problem.AddResidualBlock(
       new AutoDiffCostFunction<ExponentialResidual, 1, 1, 1>(
           new ExponentialResidual(data[2 * i], data[2 * i + 1])),
       NULL,
       &m, &c);
 }

说明：

注意，version1 与 version2 的代码区别；
使用 for循环 为每一组观测创建一个残差块；

3.2 完整代码

#include "ceres/ceres.h"
#include "glog/logging.h"

using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;
using ceres::Solve;

// Data generated using the following octave code.
//   randn('seed', 23497);
//   m = 0.3;
//   c = 0.1;
//   x=[0:0.075:5];
//   y = exp(m * x + c);
//   noise = randn(size(x)) * 0.2;
//   y_observed = y + noise;
//   data = [x', y_observed'];

const int kNumObservations = 67;
const double data[] = {
  0.000000e+00, 1.133898e+00,
  7.500000e-02, 1.334902e+00,
  1.500000e-01, 1.213546e+00,
  2.250000e-01, 1.252016e+00,
  3.000000e-01, 1.392265e+00,
  3.750000e-01, 1.314458e+00,
  4.500000e-01, 1.472541e+00,
  5.250000e-01, 1.536218e+00,
  6.000000e-01, 1.355679e+00,
  6.750000e-01, 1.463566e+00,
  7.500000e-01, 1.490201e+00,
  8.250000e-01, 1.658699e+00,
  9.000000e-01, 1.067574e+00,
  9.750000e-01, 1.464629e+00,
  1.050000e+00, 1.402653e+00,
  1.125000e+00, 1.713141e+00,
  1.200000e+00, 1.527021e+00,
  1.275000e+00, 1.702632e+00,
  1.350000e+00, 1.423899e+00,
  1.425000e+00, 1.543078e+00,
  1.500000e+00, 1.664015e+00,
  1.575000e+00, 1.732484e+00,
  1.650000e+00, 1.543296e+00,
  1.725000e+00, 1.959523e+00,
  1.800000e+00, 1.685132e+00,
  1.875000e+00, 1.951791e+00,
  1.950000e+00, 2.095346e+00,
  2.025000e+00, 2.361460e+00,
  2.100000e+00, 2.169119e+00,
  2.175000e+00, 2.061745e+00,
  2.250000e+00, 2.178641e+00,
  2.325000e+00, 2.104346e+00,
  2.400000e+00, 2.584470e+00,
  2.475000e+00, 1.914158e+00,
  2.550000e+00, 2.368375e+00,
  2.625000e+00, 2.686125e+00,
  2.700000e+00, 2.712395e+00,
  2.775000e+00, 2.499511e+00,
  2.850000e+00, 2.558897e+00,
  2.925000e+00, 2.309154e+00,
  3.000000e+00, 2.869503e+00,
  3.075000e+00, 3.116645e+00,
  3.150000e+00, 3.094907e+00,
  3.225000e+00, 2.471759e+00,
  3.300000e+00, 3.017131e+00,
  3.375000e+00, 3.232381e+00,
  3.450000e+00, 2.944596e+00,
  3.525000e+00, 3.385343e+00,
  3.600000e+00, 3.199826e+00,
  3.675000e+00, 3.423039e+00,
  3.750000e+00, 3.621552e+00,
  3.825000e+00, 3.559255e+00,
  3.900000e+00, 3.530713e+00,
  3.975000e+00, 3.561766e+00,
  4.050000e+00, 3.544574e+00,
  4.125000e+00, 3.867945e+00,
  4.200000e+00, 4.049776e+00,
  4.275000e+00, 3.885601e+00,
  4.350000e+00, 4.110505e+00,
  4.425000e+00, 4.345320e+00,
  4.500000e+00, 4.161241e+00,
  4.575000e+00, 4.363407e+00,
  4.650000e+00, 4.161576e+00,
  4.725000e+00, 4.619728e+00,
  4.800000e+00, 4.737410e+00,
  4.875000e+00, 4.727863e+00,
  4.950000e+00, 4.669206e+00,
};

struct ExponentialResidual {
  ExponentialResidual(double x, double y)
      : x_(x), y_(y) {}

  template <typename T> 
  bool operator()(const T* const m,
                  const T* const c,
                  T* residual) const {
    residual[0] = y_ - exp(m[0] * x_ + c[0]);
    return true;
  }

 private:
  const double x_;
  const double y_;
};

int main(int argc, char** argv) {
  google::InitGoogleLogging(argv[0]);

  double m = 0.0;
  double c = 0.0;

  Problem problem;
  for (int i = 0; i < kNumObservations; ++i) {
    problem.AddResidualBlock(
        new AutoDiffCostFunction<ExponentialResidual, 1, 1, 1>(
            new ExponentialResidual(data[2 * i], data[2 * i + 1])),
        NULL,
        &m, &c);
  }

  Solver::Options options;
  options.max_num_iterations = 25;
  options.linear_solver_type = ceres::DENSE_QR;
  options.minimizer_progress_to_stdout = true;

  Solver::Summary summary;
  Solve(options, &problem, &summary);
  std::cout << summary.BriefReport() << "\n";
  std::cout << "Initial m: " << 0.0 << " c: " << 0.0 << "\n";
  std::cout << "Final   m: " << m << " c: " << c << "\n";
  return 0;
}

3.3 优化过程及结果

在这里插入图片描述
上图结果显示：从参数值 $m = 0, c = 0$ 开始初始目标函数值为 $121.1734$ 以及Ceres最终找到的解决方案： $m = 0.291861, c = 0.131439$ 目标函数值为 $1.056751$ 。这些值与原始模型的参数略有不同，但在意料之中。当从噪声数据重建曲线时，我们预计会看到这样的偏差。事实上，如果你要评估目标函数 $m = 0.3, c = 0.1$ ，拟合效果较差，Ceres最终找到的解决方案： $m = 0.291838, c = 0.131567$ 目标函数值为 $1.082425$ 。下图说明了这种拟合情况：
在这里插入图片描述

在这里插入图片描述

4. Robust Curve Fitting

4.1 拟合偏离分析
上一节提供的数据均是在噪声模型中生成的点，现在假设有一些不遵循噪声模型的点，即观测数据有一些异常值，如果我们使用上面的代码来拟合这些数据，Ceres最终找到的解决方案： $m = 0.253806, c = 0.292431$ 目标函数值为 $15.13125$ 。
在这里插入图片描述
注意，拟合曲线如何偏离基本事实：(下图左上角有两个异常观测值，拟合过程需要拟合所有观测点宏观上兼顾这两个异常值使得综合后残差最小)

为了处理异常值，一种标准方法是使用 LossFunction。损失函数可以减少残差较大的残差块（通常对应于异常值）的影响。为了将损失函数与残差块关联起来，将

problem.AddResidualBlock(cost_function,
                          nullptr,
                          &m, &c);

改变为

    problem.AddResidualBlock(cost_function,
                            new CauchyLoss(0.5),
                             &m, &c);

CauchyLoss是 Ceres Solver 自带的损失函数之一。参数 $0.5$ 指定损失函数的尺度。结果，Ceres最终找到的解决方案： $m = 0.287605, c = 0.151213$ 目标函数值为 $1.902884$ 明显低于未加损失函数的拟合值 $15.13125$ 。
在这里插入图片描述
注意，拟合曲线如何移回到更接近真实曲线的位置

4.2 完整代码

#include "ceres/ceres.h"
#include "glog/logging.h"

// Data generated using the following octave code.
//   randn('seed', 23497);
//   m = 0.3;
//   c = 0.1;
//   x=[0:0.075:5];
//   y = exp(m * x + c);
//   noise = randn(size(x)) * 0.2;
//   outlier_noise = rand(size(x)) < 0.05;
//   y_observed = y + noise + outlier_noise;
//   data = [x', y_observed'];

const int kNumObservations = 67;
const double data[] = {
0.000000e+00, 1.133898e+00,
7.500000e-02, 1.334902e+00,
1.500000e-01, 1.213546e+00,
2.250000e-01, 1.252016e+00,
3.000000e-01, 1.392265e+00,
3.750000e-01, 1.314458e+00,
4.500000e-01, 1.472541e+00,
5.250000e-01, 1.536218e+00,
6.000000e-01, 1.355679e+00,
6.750000e-01, 1.463566e+00,
7.500000e-01, 1.490201e+00,
8.250000e-01, 1.658699e+00,
9.000000e-01, 1.067574e+00,
9.750000e-01, 1.464629e+00,
1.050000e+00, 1.402653e+00,
1.125000e+00, 1.713141e+00,
1.200000e+00, 1.527021e+00,
1.275000e+00, 1.702632e+00,
1.350000e+00, 1.423899e+00,
1.425000e+00, 5.543078e+00, // Outlier point
1.500000e+00, 5.664015e+00, // Outlier point
1.575000e+00, 1.732484e+00,
1.650000e+00, 1.543296e+00,
1.725000e+00, 1.959523e+00,
1.800000e+00, 1.685132e+00,
1.875000e+00, 1.951791e+00,
1.950000e+00, 2.095346e+00,
2.025000e+00, 2.361460e+00,
2.100000e+00, 2.169119e+00,
2.175000e+00, 2.061745e+00,
2.250000e+00, 2.178641e+00,
2.325000e+00, 2.104346e+00,
2.400000e+00, 2.584470e+00,
2.475000e+00, 1.914158e+00,
2.550000e+00, 2.368375e+00,
2.625000e+00, 2.686125e+00,
2.700000e+00, 2.712395e+00,
2.775000e+00, 2.499511e+00,
2.850000e+00, 2.558897e+00,
2.925000e+00, 2.309154e+00,
3.000000e+00, 2.869503e+00,
3.075000e+00, 3.116645e+00,
3.150000e+00, 3.094907e+00,
3.225000e+00, 2.471759e+00,
3.300000e+00, 3.017131e+00,
3.375000e+00, 3.232381e+00,
3.450000e+00, 2.944596e+00,
3.525000e+00, 3.385343e+00,
3.600000e+00, 3.199826e+00,
3.675000e+00, 3.423039e+00,
3.750000e+00, 3.621552e+00,
3.825000e+00, 3.559255e+00,
3.900000e+00, 3.530713e+00,
3.975000e+00, 3.561766e+00,
4.050000e+00, 3.544574e+00,
4.125000e+00, 3.867945e+00,
4.200000e+00, 4.049776e+00,
4.275000e+00, 3.885601e+00,
4.350000e+00, 4.110505e+00,
4.425000e+00, 4.345320e+00,
4.500000e+00, 4.161241e+00,
4.575000e+00, 4.363407e+00,
4.650000e+00, 4.161576e+00,
4.725000e+00, 4.619728e+00,
4.800000e+00, 4.737410e+00,
4.875000e+00, 4.727863e+00,
4.950000e+00, 4.669206e+00
};

using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::CauchyLoss;
using ceres::Problem;
using ceres::Solve;
using ceres::Solver;

struct ExponentialResidual {
  ExponentialResidual(double x, double y)
      : x_(x), y_(y) {}

  template <typename T> bool operator()(const T* const m,
                                        const T* const c,
                                        T* residual) const {
    residual[0] = y_ - exp(m[0] * x_ + c[0]);
    return true;
  }

 private:
  const double x_;
  const double y_;
};

int main(int argc, char** argv) {
  google::InitGoogleLogging(argv[0]);

  double m = 0.0;
  double c = 0.0;

  Problem problem;
  for (int i = 0; i < kNumObservations; ++i) {
    CostFunction* cost_function =
        new AutoDiffCostFunction<ExponentialResidual, 1, 1, 1>(
            new ExponentialResidual(data[2 * i], data[2 * i + 1]));
    problem.AddResidualBlock(cost_function,
                             new CauchyLoss(0.5),
                            //  nullptr,
                             &m, &c);
    /*
      ceres::LossFunction* loss_function = nullptr;
      switch (loss_function_type) {//根据选择的核函数type
      case LossFunctionType::TRIVIAL:
        loss_function = new ceres::TrivialLoss();
        break;
      case LossFunctionType::SOFT_L1:
        loss_function = new ceres::SoftLOneLoss(loss_function_scale);
        break;
      case LossFunctionType::CAUCHY:
        loss_function = new ceres::CauchyLoss(loss_function_scale);
        break;
    */
  }

  Solver::Options options;
  options.linear_solver_type = ceres::DENSE_QR;
  options.minimizer_progress_to_stdout = true;

  Solver::Summary summary;
  Solve(options, &problem, &summary);
  std::cout << summary.BriefReport() << "\n";
  std::cout << "Initial m: " << 0.0 << " c: " << 0.0 << "\n";
  std::cout << "Final   m: " << m << " c: " << c << "\n";
  return 0;
}

关于损失函数
Ceres包含许多预定义的损失函数。下图演示了图形的形状。更多的细节可以在include/ceres/loss_function.h中找到。

常见损失函数：

class TrivialLoss $\rho(s)=s$
class HuberLoss $\rho(s)=\begin{cases}s \qquad \qquad s\leqslant1\\ 2\sqrt s -1 \quad s\leqslant1 \end{cases}$
class SoftLOneLoss $\rho(s)=2(\sqrt{1+s}-1)$
class ArctanLoss $\rho(s)=arctan(s)$
class TolerantLoss $\rho(s,a,b)=b\log(1+e^{\frac{(s-a)}{b}})-b\log(1+e^{-\frac{a}{b}})$

用法：
  ceres::LossFunction* loss_function = nullptr;
     switch (loss_function_type) {//根据选择的核函数type
    case LossFunctionType::TRIVIAL:
      loss_function = new ceres::TrivialLoss();
         break;
      case LossFunctionType::SOFT_L1:
        loss_function = new ceres::SoftLOneLoss(loss_function_scale);
        break;
     case LossFunctionType::CAUCHY:
        loss_function = new ceres::CauchyLoss(loss_function_scale);
        break;