DES算法原理

1. 对称密码算法中的分组加密算法（对应于流密码）

2. 密钥64位，56位参与运算+8位校验位（校验位为：8、16、24、32、40、48、56、64）

加密原理

1. IP置换

将明文数据转化为二进制数，并将它们按照每64bit/组分开。IP置换就是通过按照初始置换表中对应的索引找到对应的64bit中的索引值进行替换，例子如下图：

2. 轮函数

经过简单的变化位置后就来到了DES算法的核心加解密数据块区，全局加密流程如下图，图中可以看到由经过初始置换后的64bit -> 2组 * 32bit，然后以组32bit进行操作

2.1 E扩展置换

将32bit数据 -> 8组 * 4bit再对每组的首位增添1bit，其中首bit是前一组的最后一bit，尾bit是后一个组的首个bit，使最后的数据扩展为8组 * 6bit 也就是48bit，这样就完成了对32bit扩展置换为48bit。具体如图所示：

2.2 S盒压缩处理

经过扩展后的48bit再通过与48位的子密钥（加密算法开始接触密钥，在这之前用于加解密的key也已经通过加密算法生成了一个密钥）进行异或处理。

将异或后的48bit进行分组 -> 8组 * 6bit ，对每组的6bit压缩成为4bit，具体实现如图所示：

根据上面的计算得到了坐标为（3，15）的数据，那么再根据S盒表进行查找得到对应的码表值，部分S盒表如图：

（8次轮函数加密对应S₁-S₈）

根据坐标找到的值为13，将13（十） —> 1101（二），那么bin(“111111”) -> S盒压缩后 -> bin(“1101”) ，这样就完成了一轮压缩，由进入压缩前的48bit -> 32bit 。但是不会马上进入到第二轮而是进入到P盒置换

2.3 P盒置换

P盒置换和第一次的IP置换一样根据表中的值填入数据的索引值，如图：

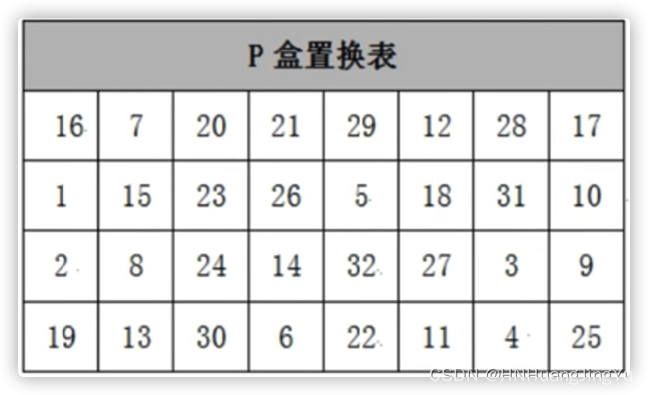
那么此时32bit的数据经过移位置换操作后，再通过8次S盒压缩处理，最后将该32bit数据（已轮加密后）对L₀（L0是首次对64bit数据分出来的一组数据32bit）进行异或就得到R1 即 $ R_1= L_0\ xor f(R_0,k) $ （f(R0,k)表示通过密钥轮加密的值） 这样就完成了第一轮函数加密 ，按照 $L_1=R_0$，$ R_1= L_0\ xor f(R_0,k) $ 每次下标自增1在经过16次轮加密后(也就是$L_{16}=R_{15}$，$ R_{16}= L_{15}\ xor f(R_{15},k) $)就得到了R₁₆ 和L₁₆ 完成16轮迭代

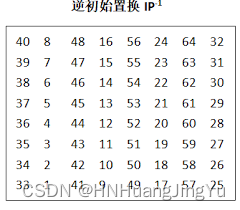
3. 逆置换

最后通过和首次的置换方法一样通过如下表中的值对数据进行索引取值，再进行替换最终得到明文64bit加密后的密文64bit完成一组加密。逆置换表如图：

密钥生成

在对一个明文使用DES加密时需要一个密钥，而这个密钥同样用于解密密文

密钥生成流程图：

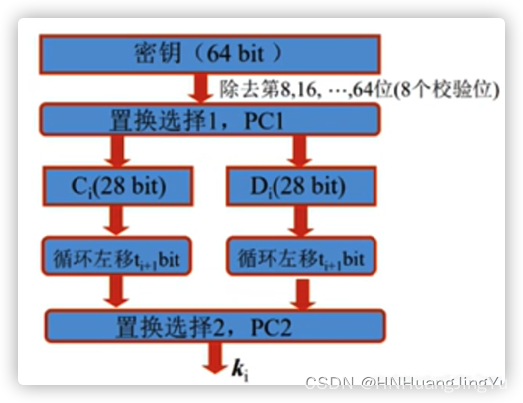
1. 首先经过如下图PC-1表，进行置换前去掉校验位（8、16、24、32、40、48、56、64）也就是每组的最后一个bit被去掉，得到56bit（可以看到PC-1表中并没有校验位的索引）

2. 再通过对56bit进行分组为 2 * 28bit 表示为C_iD_i分别对2组的数据进行移位操作，如图移位次数表。对应下列表中的左移值可得出$C_1=C_0<<1$ 同理$D_1=D_0<<1$

3. 得到C1 和 D1后将C1D1的二进制拼接后得到一个56bit值，通过如图PC-2表进行置换，从表中可以注意到PC-2表只有48位，从而也就将56bit压缩成了48bit最终得到k₁

4. 整体流程梳理图：

经过上图中的迭代重复16次后即可得到k1 -k16的数据作为最终的密钥，再配合算法进行明文加密