参考：推荐系统（三）Factorization Machines（FM）_svmmf-CSDN博客

一句话概括下FM：隐式向量特征交叉----类似embedding的思想

LR

如果利用LR做特征的二阶交叉，有：

但这个公式存在显著缺点：

1. 时间段复杂度是O(N^2)。

2. 依赖于xixj特征对的共现，如果这个特征对在训练集中没有出现，那么wij这个参数学习不到。

SVM

支持向量机的核心：低维空间下无法找到一个超平面来划分两类样本，那么可以经过一个映射，把低维空间映射成高维空间来找到一个超平面划分样本

原始公式为：

如果要实现特征交叉，利用核函数

1.线性核函数 k = <xi , xj>+1

2. 多项式核函数

还是同LR一样有显著的缺点：
交叉项的参数是独立的，这会使得如果这个交叉特征值没有在样本里出现，这个参数是无法学到的。

总结一下，主要存在两个难点：

• 交叉特征 xixj 的参数独立，如果交叉特征值没有出现，那么参数无法学习。

• 时间复杂度过高，如果直接做二阶交叉，时间复杂度为O(N^2)。

FM

基本原理

FM则解决了上面两个问题，公式为：

将wij分解成了<vi ,vj>，通过学习每一个特征对应的隐向量（embedding向量），不再依赖于交叉特征xixj的共现信息，因为即使没有共现，对应的<vi ,vj>依然能够得到训练。

推导过程

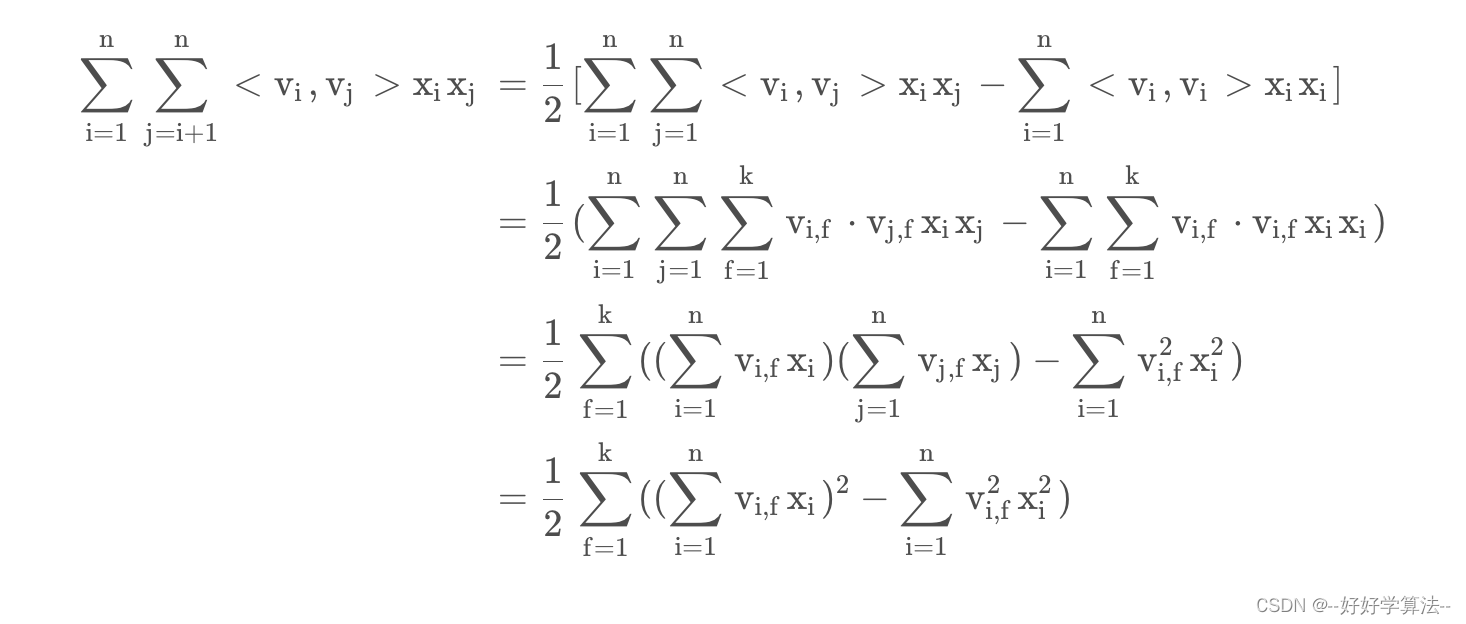
时间复杂度由O(n^2)降到O(KN)

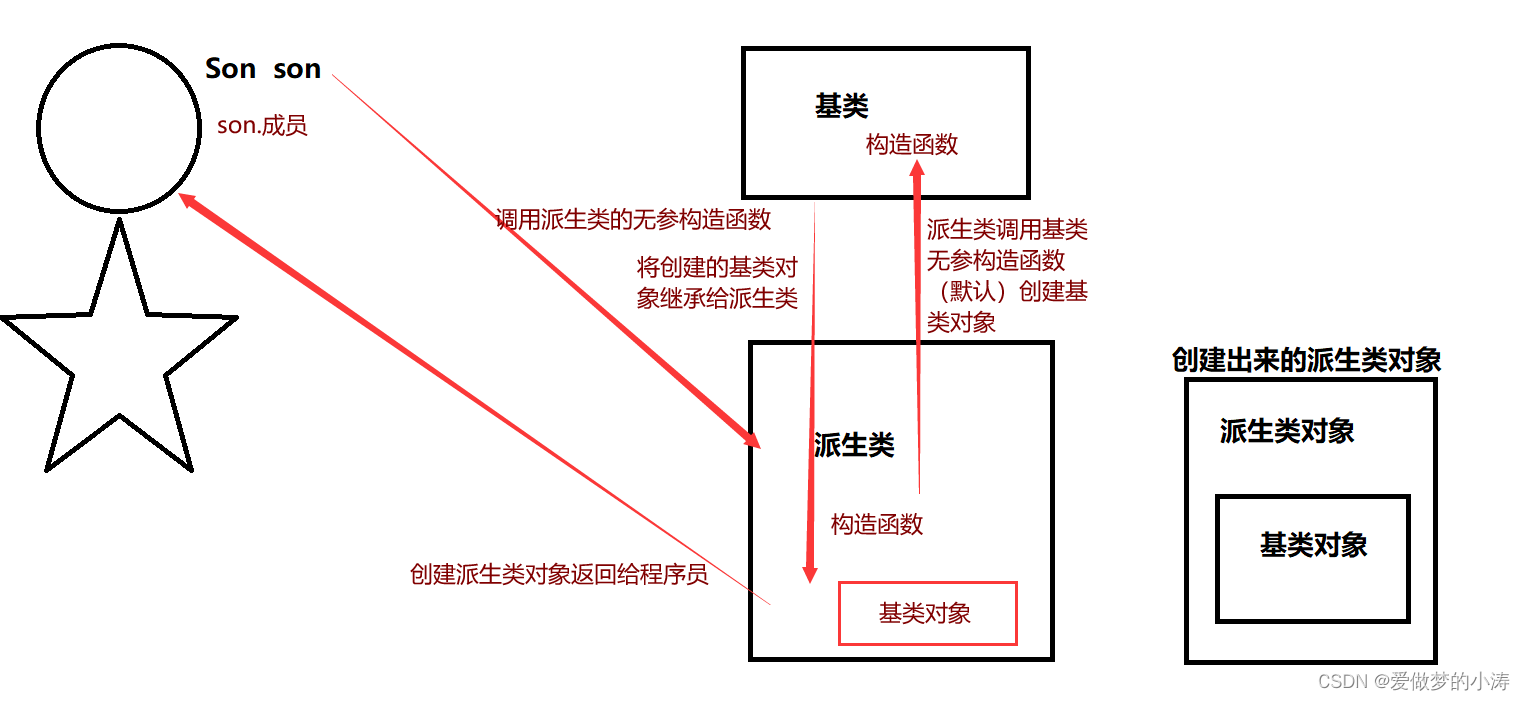
思想来源-MF

矩阵分解MF（matrix factorization），在推荐系统里，每个用户对每个物品的评分，可以构建出一个user-item矩阵，而矩阵分解的核心思想是用一个用户embedding矩阵和一个物品embedding矩阵的乘积来近似这个大矩阵，这两个embedding矩阵是可训练学习的。