目录

一、实验目的

二、问题描述

三、实验要求

四、算法思想

1.  基准算法

1.1 算法思想

1.2 代码

1.3 时间复杂度

2. 使用并查集的高效算法

2.1 算法思想

2.2 代码：

2.3 时间复杂度：

五、实验结果

---

一、实验目的

1. 掌握图的连通性。

2. 掌握并查集的基本原理和应用。

二、问题描述

在图论中，一条边被称为“桥”代表这条边一旦被删除，这个图的连通块数量会增加。等价地说，一条边是一座桥当且仅当这条边不在任何环上，一个图可以有零或多座桥。现要找出一个无向图中所有的桥，基准算法为：对于图中每条边uv，删除该边后，运用BFS或DFS确定u和v是否仍然连通，若不连通，则uv是桥。应用并查集设计一个比基准算法更高效的算法，不要使用Tarjan算法。        

                                    

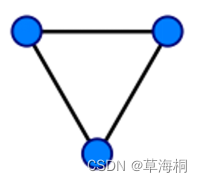
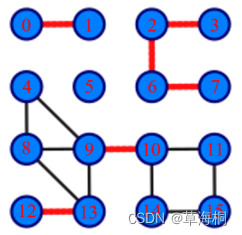
            图1 没有桥的无向连通图                   图2 有16个顶点和6个桥的图（桥以红色线段标示）

三、实验要求

1. 实现上述基准算法。

2. 设计的高效算法中必须使用并查集，如有需要，可以配合使用其他任何数据结构。

3. 用图2的例子验证算法的正确性，该图存储在smallG.txt中，文件中第1行是顶点数，第2行是边数，后面是每条边的两个端点。

4. 使用文件mediumG.txt和largeG.txt中的无向图测试基准算法和高效算法的性能，记录两个算法的运行时间。

5. 实验课检查内容：对于smallG.txt、mediumG.txt、largeG.txt中的无向图，测试高效算法的输出结果和运行时间，检查该代码，限用C或C++语言编写。其中smallG.txt和mediumG.txt为必做内容，运行时间在4分钟内有效，直接在终端输出结果和运行时间。以smallG.txt为例，输出如下：

6

0 1

2 3

2 6

6 7

9 10

12 13

0.002

其中，第一行的6表示桥数，接下来的6行分别是6座桥的两个端点，小端点在前，大端点在后，6座桥按照端点从小到大的顺序输出，最后一行的0.002为整个main函数的运行时间，单位为秒。

四、算法思想

1.  基准算法

1.1 算法思想

        1）先dfs遍历图，得到连通分量个数N；

        2）遍历边集，对于每条边ei，先删除ei；

        3）再次dfs得到此时的连通分量个数num，

        4）如果num!=N，则ei为桥；否则不为桥。

        5）恢复ei，取下一条边ei+1，回到2）继续，直到遍历完全部边。

1.2 代码

int **k,*v,n,m,**br,brnum,N;
//邻接矩阵、访问位、点数、边数、是否为桥、桥数、
int *p,*d,*qiao;//并查集、点的深度、标记dfs2后是否为桥
string filename;//文件名

void read1(){//初始化
	int i,a,b;
	ifstream file(filename.c_str());
	file>>n>>m;
	k=new int*[n];
	v=new int[n];
	br=new int*[n];
	brnum=0;
	for(i=0;i<n;i++){
		k[i]=new int[n];
		br[i]=new int[2];
		v[i]=0;
		br[i][0]=br[i][1]=0;
		for(int j=0;j<n;j++)
			k[i][j]=0;
	}
	for(i=0;i<m;i++){
		file>>a>>b;
		k[a][b]=1;
		k[b][a]=1;
	}
	file.close();
}

void dfs1(int a){//dfs深度遍历
	int i;
	v[a]=1;
	for(i=0;i<n;i++)
		if(k[a][i]&&!v[i])
			dfs1(i);
}

int count1(){//计算连通分量个数
	int i,num=0;
	for(i=0;i<n;i++)
		if(!v[i]){
			dfs1(i);
			num++;
		}
 	return num;
}

void base(){//基准法
	int i,j,a,b,num;
	ifstream file(filename.c_str());
	file>>n>>m;
	N=count1();
	for(i=0;i<m;i++){
		file>>a>>b;
		k[a][b]=0;//先删除该边
		k[b][a]=0;
		for(j=0;j<n;j++)
			v[j]=0;
		num=count1();
		if(num!=N){//判断是否为桥
			br[brnum][0]=a;//记录桥
			br[brnum][1]=b;
			brnum++;//桥个数增加
		}
		k[a][b]=1;//恢复该边
		k[b][a]=1;
	}
	file.close();
}

void print1(){//因为实验对输出格式有要求
	int i,j,a,b;
	cout<<brnum<<endl;
	for(i=0;i<brnum-1;i++){//选择排序
		a=i;
		for(j=i+1;j<brnum;j++){
			if(br[j][0]<br[a][0]||
				(br[j][0]==br[a][0]&&br[j][1]<br[a][1]))
				//父端较小 或 父端相同、子端较小
			a=j;
		}
		b=br[a][0];
		br[a][0]=br[i][0];
		br[i][0]=b;
		b=br[a][1];
		br[a][1]=br[i][1];
		br[i][1]=b;
	}
	for(int i=0;i<brnum;i++){
		cout<<br[i][0]<<" "<<br[i][1]<<endl;
	}
}

1.3 时间复杂度

        n个点，m条边。需要遍历m条边，O(m)，每次都需要count1一次，而count1由于是使用邻接矩阵储存边关系，最坏情况为O(n^2)。所以总的时间复杂度为O(m*n^2)。

        如果用邻接表，则count1的时间复杂度为O(n+m)，总时间复杂度变为O(m(n+m))。

2. 使用并查集的高效算法

2.1 算法思想

        桥的等价意义：不在环上的边。

        树是边数最小的无环图，当向树上添加任意一条顶点都在树上的边时，会形成环。桥不在环上，所以桥只能在图的生成树上。

        所以还是先构建生成树，然后不断dfs，不过dfs过程中顺便记录每个点的深度d[i]。

        再遍历所有边，每次遍历时：

                如果为生成树上的边则直接return。

                否则：求当前边两端点的最近公共祖先（LCA），过程中将路过的边（在环上）置为非桥边（q[i]==0）；并根据LCA进行路径压缩compress（将环上除了LCA本身的点的父节点均设置为LCA）。

        这里以点带边，即q[i]==1表示以第i个点为尾的生成树上的边为桥，该边用(p[i],i)表示（p[i]为i在生成树上的父节点）。

2.2 代码：

void read2(){//读入文件信息并初始化
	…………
}

void dfs2(int a,int b,int depth){//b is the ancestor of a
	…………
}

void count2(){//生成生成树、并查集、深度集合等
	…………
}

void compress(int x,int a){//路径压缩
	if(p[x]==a)//等于最近公共祖先
		return;
 	else{
 		int t=x;
 		x=p[x];
 		p[t]=a;
 		compress(x,a);
	}
}

void LCA(int a,int b){//对每条边的两点找最近公共祖先
	if(p[a]==b||p[b]==a)//在生成树上的边，直接返回
		return;
	else{
		int u=a,v=b,//保留原边的两端
			x=0,y=0;//判断a、b是否在while中执行了a=p[a]、b=p[b]操作，有执行才压缩，
					//避免其中一点是最近公共祖先时压缩导致该点父节点被自己覆盖
		while(1){
			if(d[a]>d[b]){//深度大的向上遍历
				qiao[a]=0;
				a=p[a];
				x=1;
			}
			else if(d[a]<d[b]){//深度大的向上遍历
				qiao[b]=0;
				b=p[b];
				y=1;
			}
			else if(a!=b){//深度相同但不同点，一起向上遍历
				qiao[a]=0;
				qiao[b]=0;
				a=p[a];
				b=p[b];
				x=y=1;
			}
			else break;//同个点，a=b=最近公共祖先
		}
        //此时a==b
		if(x)//路径压缩
		compress(u,a);
		if(y)
		compress(v,b);
	}
}
void better(){//并查集的高效算法
	int i,a,b;
	ifstream file(filename.c_str());//读入文件
	count2();//生成生成树、并查集、深度集合等
	file>>n>>m;
	for(i=0;i<m;i++){//遍历每一条边
		file>>a>>b;
		LCA(a,b);//求最近公共祖先
	}
	file.close();
}
void print2(){//打印输出
	……
}

     虽然压缩后不能再直接使用”if(p[a]==b||p[b]==a)“判断边(a,b)是否为原生成树上的边，但不影响结果。因为压缩的边都是非桥边，只不过会执行下面的while。但总体上压缩后效率还是提高了的。

2.3 时间复杂度：

        n个点，m条边。dfs构建生成树最坏情况下时间复杂度为O(n^2)。遍历m条边，每次查找最近公共祖先最差情况下要查找n次，时间复杂度为O(n)，一次路径压缩最差情况时间复杂度也为O(n)。所以总时间复杂度为O(n*(m+n))。

​

五、实验结果

1、用图2的例子验证算法的正确性，该图存储在smallG.txt中，文件中第1行是顶点数，第2行是边数，后面是每条边的两个端点。

                                                  

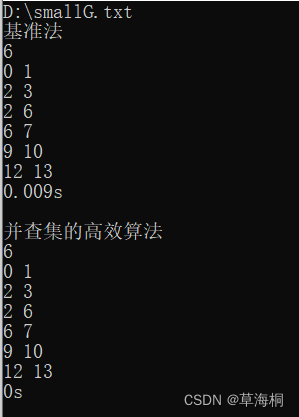
        验证正确。

2、使用文件mediumG.txt和largeG.txt中的无向图测试基准算法和高效算法的性能，记录两个算法的运行时间。

        mediumG.txt：

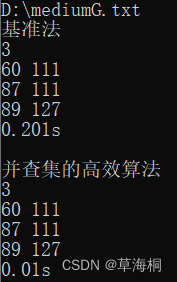
       对于largeG.txt文件，由于使用的是邻接矩阵，n太大，运行时内存不够分配，运行中断。