文章目录
- 1.神经网络
- 1.1 可视化数据
- 1.2 模型表示
- 1.3 前馈和成本函数
- 1.4 正则化代价函数
- 2.反向传播
- 2.1 Sigmoid的导数
- 2.2随机初始化
- 2.3 反向传播
- 2.4梯度检测
- 2.5 正则化神经网络
- 2.6 优化参数
- 3.可视化隐藏层
1.神经网络
在上一个练习中,您为神经网络实现了前馈传播,并利用我们提供的权重来预测手写数字。在本练习中,您将实现反向传播算法来学习神经网络的参数。
提供的脚本 ex4.m 将帮助您逐步完成本练习。
1.1 可视化数据
在 ex4.m 的第一部分中,代码将加载数据并通过调用函数 displayData 将其显示在二维图上(图 1)。
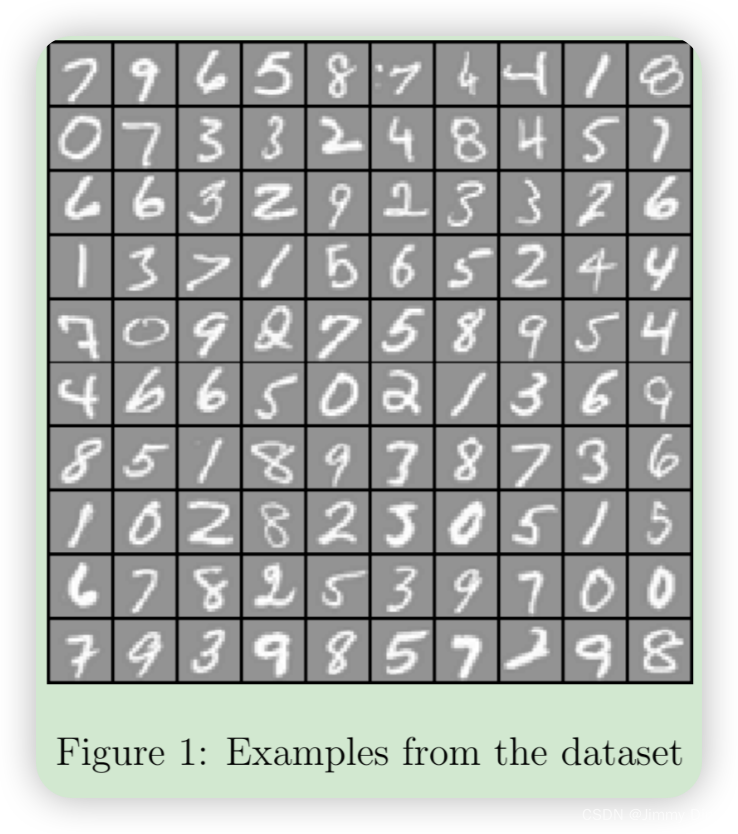
这是您在上一个练习中使用的相同数据集。ex3data1.mat 中有 5000 个训练示例,其中每个训练示例都是 20 像素 x 20 像素的数字灰度图像。每个像素都由一个浮点数表示,表示该位置的灰度强度。20 x 20 像素网格被“展开”为 400 维向量。这些训练示例中的每一个都成为数据矩阵 X 中的一行。这为我们提供了一个 5000 x 400 矩阵 X,其中每一行都是手写数字图像的训练示例。

训练集的第二部分是一个 5000 维向量 y,其中包含训练集的标签。为了与 Octave/MATLAB 索引(其中没有零索引)更兼容,我们将数字零映射到值十。因此,“0”数字被标记为“10”,而“1”到“9”的数字按其自然顺序标记为“1”到“9”。
与上一节作业几乎一样
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
import scipy.optimize as opt
from sklearn.metrics import classification_report # 这个包是评价报告
def load_mat(path):
'''读取数据'''
data = loadmat('ex4data1.mat') # return a dict
X = data['X']
y = data['y'].flatten()
return X, y
def plot_100_images(X):
"""随机画100个数字"""
index = np.random.choice(range(5000), 100) # 从范围5000中随机选择100个索引
images = X[index] # 根据随机索引选择100个图像
fig, ax_array = plt.subplots(10, 10, sharey=True, sharex=True, figsize=(8, 8)) # 创建一个10x10的子图,所有子图共享x轴和y轴,图像大小为8x8英寸
for r in range(10): # 遍历10行
for c in range(10): # 遍历10列
ax_array[r, c].matshow(images[r*10 + c].reshape(20,20).T, cmap='gray_r') # 将每个图像重塑为20x20并转置,然后在子图中显示为反转的灰度图
plt.xticks([]) # 去除x轴刻度
plt.yticks([]) # 去除y轴刻度
plt.show() # 显示图像
X,y = load_mat('ex4data1.mat')
plot_100_images(X)
如图

1.2 模型表示
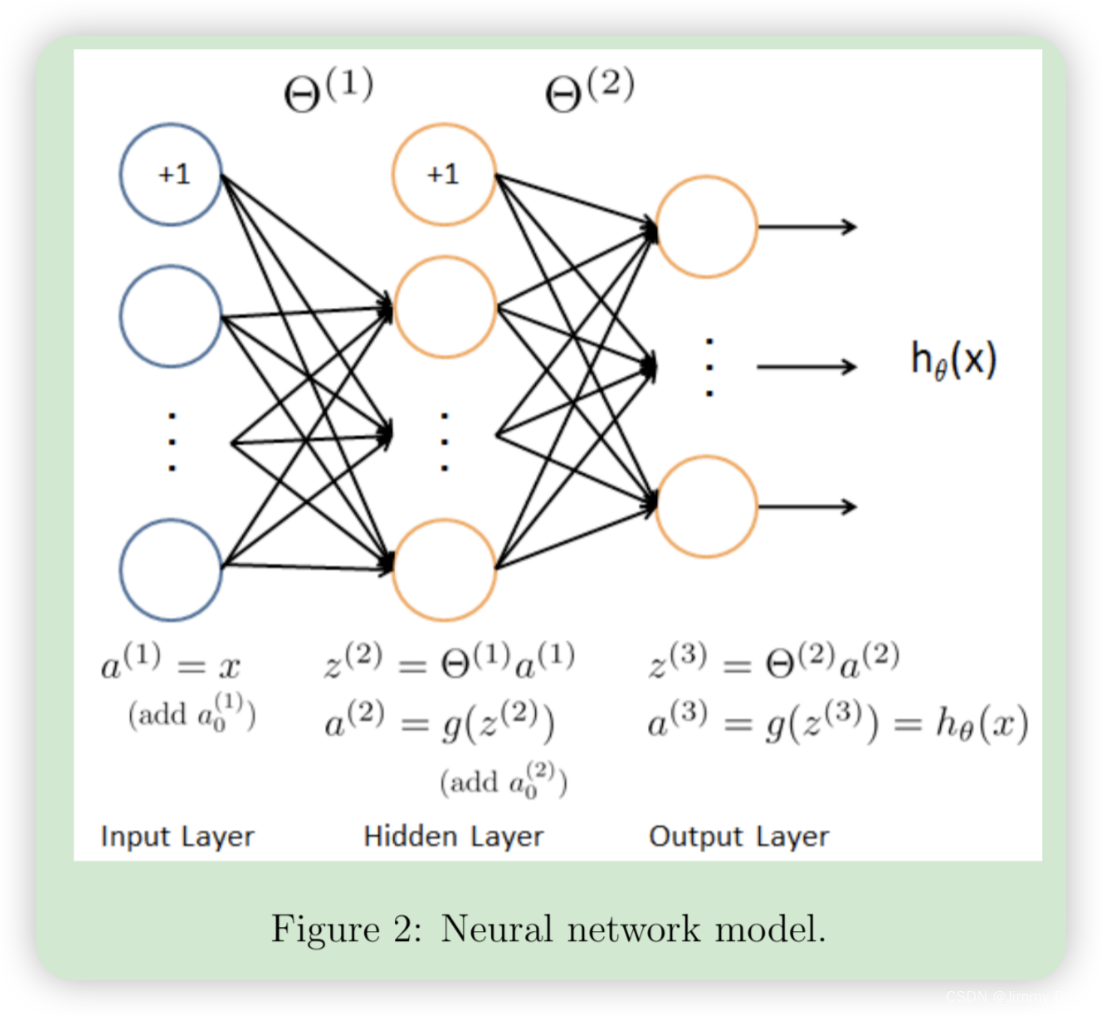
我们的神经网络如图 2 所示。它有 3 层——输入层、隐藏层和输出层。回想一下,我们的输入是数字图像的像素值 3。由于图像的大小为 20 × 20,因此我们有 400 个输入层单元(不计算始终输出 +1 的额外偏置单元)。训练数据将由 ex4.m 脚本加载到变量 X 和 y 中。
我们已为您提供一组经过训练的网络参数(Θ(1)、Θ(2))。这些参数存储在 ex4weights.mat 中,并将由 ex4.m 加载到 Theta1 和 Theta2 中。这些参数的尺寸适合第二层有 25 个单元和 10 个输出单元(对应 10 个数字类别)的神经网络。
from sklearn.preprocessing import OneHotEncoder
def expand_y(y):
result = []
# 把y中每个类别转化为一个向量,对应的label值在向量对应位置上置为1
for i in y:
y_array = np.zeros(10) # 创建一个长度为10的全零向量
y_array[i-1] = 1 # 将对应类别的位置置为1
result.append(y_array) # 将转换后的向量添加到结果列表中
'''
# 或者用sklearn中OneHotEncoder函数
encoder = OneHotEncoder(sparse=False) # 使用OneHotEncoder并设置sparse=False以返回数组而不是矩阵
y_onehot = encoder.fit_transform(y.reshape(-1, 1)) # 将y转换为二维数组并进行独热编码
return y_onehot # 返回独热编码后的数组
'''
return np.array(result) # 将结果列表转换为NumPy数组并返回
# 加载数据的函数
def load_mat(path):
data = loadmat(path)
return data['X'], data['y']
# 调用load_mat函数加载数据
raw_X, raw_y = load_mat('ex4data1.mat')
# 在特征矩阵X的第一列插入全1列,用于偏置项
X = np.insert(raw_X, 0, 1, axis=1)
# 将标签y进行独热编码
y = expand_y(raw_y)
# 打印X和y的形状
X.shape, y.shape
'''
((5000, 401), (5000, 10))
'''
def load_weight(path):
data = loadmat(path) # 使用loadmat函数加载指定路径的MAT文件
return data['Theta1'], data['Theta2'] # 返回文件中的Theta1和Theta2
# 从文件中加载预训练的权重
t1, t2 = load_weight('ex4weights.mat')
# 查看权重矩阵的形状
t1.shape, t2.shape
# 预期输出: ((25, 401), (10, 26))
def serialize(a, b):
'''展开参数'''
return np.r_[a.flatten(), b.flatten()]
def deserialize(seq):
'''提取参数'''
return seq[:25*401].reshape(25, 401), seq[25*401:].reshape(10, 26)
# 扁平化参数,25*401+10*26=10285
theta = serialize(t1, t2)
theta.shape # (10285,)
1.3 前馈和成本函数
现在,你将实现神经网络的成本函数和梯度。首先,完成 nnCostFunction.m 中的代码以返回成本。回想一下,神经网络的成本函数(无正则化)是
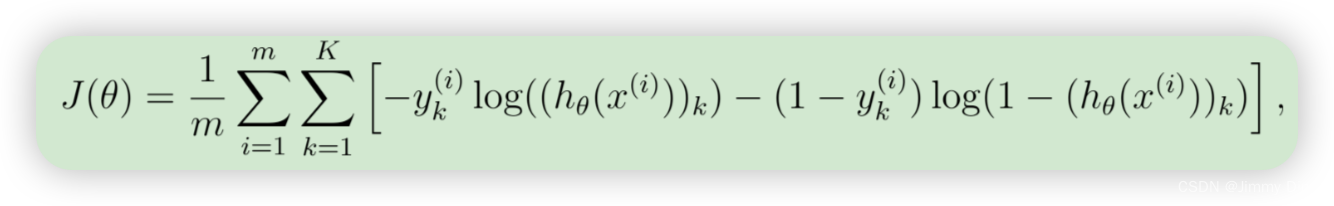
其中 hθ(x(i)) 的计算方式如图 2所示,K = 10 是可能的标签总数。请注意,hθ(x(i))k = a(3) k 是第 k 个输出单元的激活值(输出值)。另外,回想一下,虽然原始标签(在变量 y 中)是 1、2、…、10,但为了训练神经网络,我们需要将标签重新编码为仅包含值 0 或 1 的向量,因此
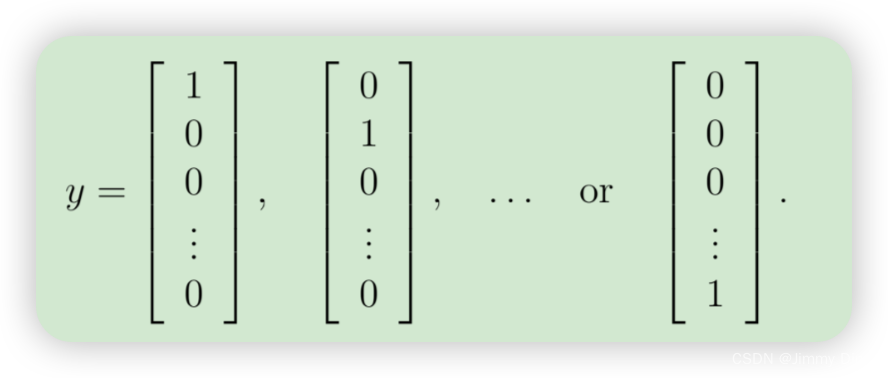
您应该实现前馈计算,为每个示例 i 计算 hθ(x(i)),并将所有示例的成本相加。您的代码还应该适用于任意大小、任意数量标签的数据集(您可以假设始终至少有 K ≥ 3 个标签)。
实现说明:矩阵 X 包含行中的示例(即 X(i,:)’ 是第 i 个训练示例 x (i),表示为 n × 1 向量。)完成 nnCostFunction.m 中的代码后,您需要将 1 的列添加到 X 矩阵。神经网络中每个单元的参数在 Theta1 和 Theta2 中表示为一行。具体而言,Theta1 的第一行对应于第二层中的第一个隐藏单元。您可以使用 for 循环遍历示例来计算成本。
import numpy as np
def sigmoid(z):
'''计算sigmoid函数'''
return 1 / (1 + np.exp(-z))
def feed_forward(theta, X):
'''计算每层的输入和输出'''
t1, t2 = deserialize(theta) # 将展开的一维参数还原为权重矩阵
a1 = X # 输入层的激活值,即输入数据
z2 = a1 @ t1.T # 计算隐藏层的输入,a1与第一层权重矩阵t1的转置相乘
a2 = np.insert(sigmoid(z2), 0, 1, axis=1) # 计算隐藏层的激活值,并插入偏置单元
z3 = a2 @ t2.T # 计算输出层的输入,a2与第二层权重矩阵t2的转置相乘
a3 = sigmoid(z3) # 计算输出层的激活值,即网络的预测结果
return a1, z2, a2, z3, a3 # 返回每层的输入和输出
# 调用 feed_forward 函数进行神经网络的前向传播
a1, z2, a2, z3, h = feed_forward(theta, X)
# 在这里:
# theta 是神经网络的权重参数
# X 是输入的特征矩阵
# 返回值包括:
# a1: 输入层的激活值
# z2: 第一个隐藏层的加权输入
# a2: 第一个隐藏层的激活值
# z3: 输出层的加权输入
# h: 神经网络的预测输出
def cost(theta, X, y):
# 使用 feed_forward 函数计算神经网络的前向传播结果
a1, z2, a2, z3, h = feed_forward(theta, X)
# 初始化损失函数 J
J = 0
# 遍历每一个样本
for i in range(len(X)):
# 计算交叉熵损失的第一部分
first = - y[i] * np.log(h[i])
# 计算交叉熵损失的第二部分
second = (1 - y[i]) * np.log(1 - h[i])
# 将第一部分和第二部分求和累加到总损失 J 中
J = J + np.sum(first - second)
# 计算平均损失
J = J / len(X)
# 返回平均损失 J
return J
'''
# or just use vectorization
J = - y * np.log(h) - (1 - y) * np.log(1 - h)
return J.sum() / len(X)
'''
这段代码用一行简洁地实现了与上述循环代码相同的功能,但使用了向量化操作,这在计算上通常更有效率和简洁。
1.4 正则化代价函数
具有正则化的神经网络的成本函数由下式给出:
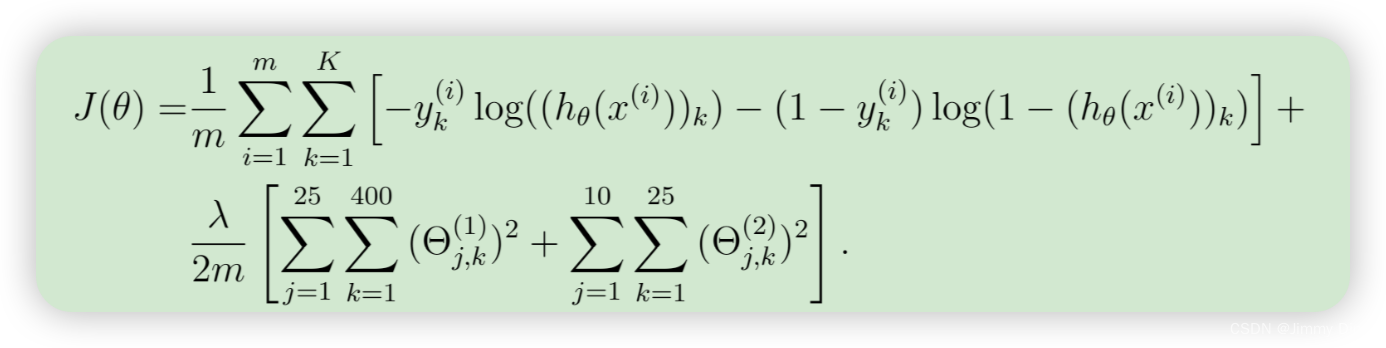
您可以假设神经网络只有 3 层 - 输入层、隐藏层和输出层。但是,您的代码应该适用于任意数量的输入单元、隐藏单元和输出单元。虽然我们已明确列出了 Θ(1) 和 Θ(2) 的索引以便于理解,但请注意,您的代码通常适用于任何大小的 Θ(1) 和 Θ(2)。请注意,您不应该正则化对应于偏差的项。对于矩阵 Theta1 和 Theta2,这对应于每个矩阵的第一列。您现在应该将正则化添加到成本函数中。请注意,您可以先使用现有的 nnCostFunction.m 计算未正则化的成本函数 J,然后再添加正则化项的成本。完成后,ex4.m 将使用已加载的 Theta1 和 Theta2 参数集以及 λ = 1 调用您的 nnCostFunction。您应该看到成本约为 0.383770。
# 定义正则化损失函数
def regularized_cost(theta, X, y, l=1):
'''正则化时忽略每层的偏置项,也就是参数矩阵的第一列'''
# 反序列化 theta 为两个参数矩阵 t1 和 t2
t1, t2 = deserialize(theta)
# 计算正则化项(不包括偏置项),即每层参数矩阵的第一列被忽略
reg = np.sum(t1[:,1:] ** 2) + np.sum(t2[:,1:] ** 2) # 也可以使用 np.power(a, 2) 函数
# 计算正则化损失值
return l / (2 * len(X)) * reg + cost(theta, X, y)
regularized_cost(theta, X, y, 1) # 0.38376985909092354
2.反向传播
在本练习的这一部分,您将实现反向传播算法,以计算神经网络成本函数的梯度。您需要完成nnCostFunction.m文件,以便它返回适当的梯度值grad。一旦计算出梯度,您就可以使用高级优化器(如fmincg)来最小化成本函数J(θ)来训练神经网络。
您将首先实现反向传播算法,以计算(未正则化)神经网络参数的梯度。在您已验证未正则化情况下的梯度计算正确之后,您将实现正则化神经网络的梯度。
2.1 Sigmoid的导数
为了帮助您开始练习的这一部分,您将首先实现s型梯度函数。s型函数的梯度可以是
计算为
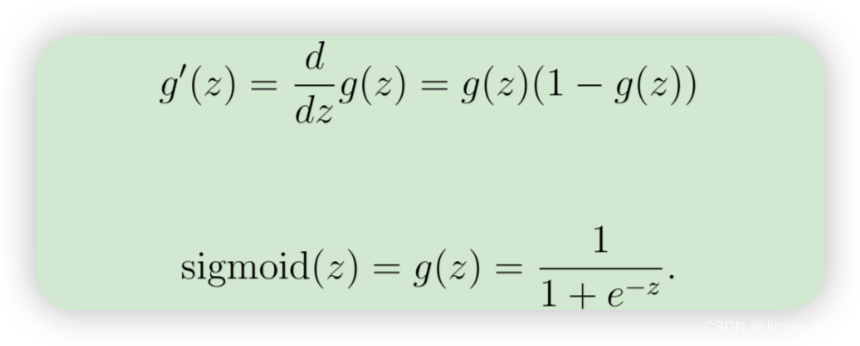
def sigmoid_gradient(z):
return sigmoid(z) * (1 - sigmoid(z))
2.2随机初始化
在训练神经网络时,随机初始化参数对于打破对称性非常重要。随机初始化的一个有效策略是在 [-init, init] 范围内均匀地随机选择 Θ(l) 的值。
你应该使用 init = 0.12这个取值范围可以确保参数保持在较小的范围内,并提高学习效率。你的任务是完成 randInitializeWeights.m 来初始化 Θ 的权重;修改该文件并填写以下代码:

def random_init(size):
'''从服从的均匀分布的范围中随机返回size大小的值'''
return np.random.uniform(-0.12, 0.12, size)
2.3 反向传播
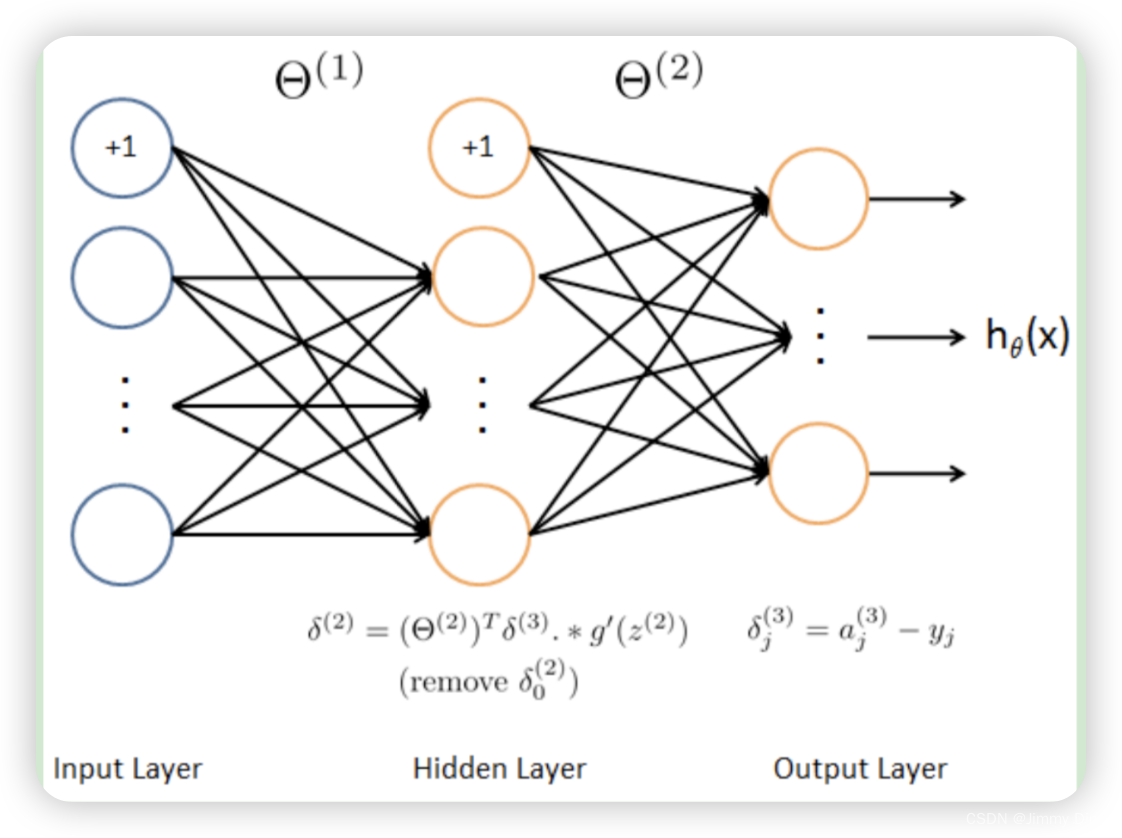
现在,你将实现反向传播算法。回顾一下:
反向传播算法的原理如下。给定一个训练示例(x(t), y(t)),我们将首先运行 “前向传递”,计算整个网络的所有激活,包括假设 hΘ(x) 的输出值。然后,对于第 l 层的每个节点 j,我们要计算一个 "误差项 "δ (l)j,以衡量该节点对输出中的任何误差 "负责 "的程度。对于输出节点,我们可以直接测量网络激活与真实目标值之间的差值,并用它来定义δ (3)j(因为第 3 层是输出层)。对于隐藏单元,您将根据第 (l + 1) 层节点误差项的加权平均值来计算 δ(l)j。您应该在一个每次处理一个示例的循环中实现步骤 1 至 4。具体来说,您应该为 t = 1:m 实现一个 for 循环,并将下面的 1-4 步放在 for 循环中,第 t 次迭代对第 t 个训练示例(x(t), y(t))进行计算。步骤 5 将累积梯度除以 m,得到神经网络成本函数的梯度。
- 将输入层的值(a(1))设置为第 t 个训练示例 x(t)。执行前馈传递(图 2),计算第 2 层和第 3 层的激活度(z(2), a(2), z(3), a(3))。请注意,您需要添加一个 +1 项,以确保层 a (1) 和 a (2) 的激活向量也包括偏置单元。在 Octave/MATLAB 中,如果 a 1 是一个列向量,则加 1 相当于 a 1 = [1 ; a 1]。
- 对于第 3 层(输出层)的每个输出单元 k,设置
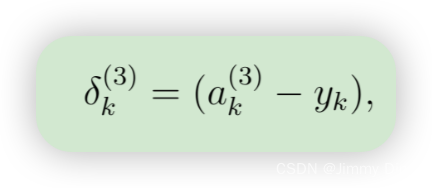
- 对于隐层 l = 2,设置
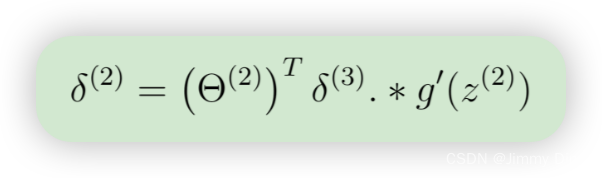
- 使用以下公式计算本例中的梯度。在 Octave/MATLAB 中,删除 δ 相当于 delta 2 = delta 2(2:end)
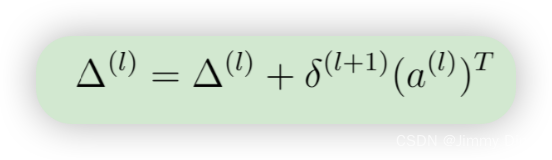
- 将累积梯度除以 1/m,得到神经网络成本函数的(非正规化)梯度
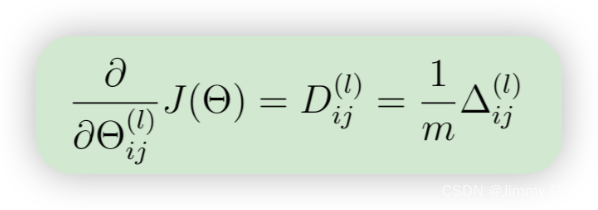
print('a1', a1.shape, 't1', t1.shape)
print('z2', z2.shape)
print('a2', a2.shape, 't2', t2.shape)
print('z3', z3.shape)
print('a3', h.shape)
'''
a1:输入层的激活值(包括偏置项)。形状为 (5000, 401),表示有5000个样本,每个样本有401个特征(包括偏置项)。
t1:第一个隐藏层的权重矩阵。形状为 (25, 401),表示第一个隐藏层有25个神经元,每个神经元有401个输入(包括偏置项)。
z2:第一个隐藏层的加权输入值。形状为 (5000, 25),表示5000个样本,每个样本有25个加权输入值。
a2:第一个隐藏层的激活值(包括偏置项)。形状为 (5000, 26),表示5000个样本,每个样本有26个激活值(包括偏置项)。
t2:输出层的权重矩阵。形状为 (10, 26),表示输出层有10个神经元,每个神经元有26个输入(包括偏置项)。
z3:输出层的加权输入值。形状为 (5000, 10),表示5000个样本,每个样本有10个加权输入值。
a3 (h):输出层的激活值(预测输出)。形状为 (5000, 10),表示5000个样本,每个样本有10个预测输出。
'''
def gradient(theta, X, y):
'''
unregularized gradient, notice no d1 since the input layer has no error
return 所有参数theta的梯度,故梯度D(i)和参数theta(i)同shape,重要。
'''
# 反序列化 theta 为两个参数矩阵 t1 和 t2
t1, t2 = deserialize(theta) # 将参数向量theta分解为t1和t2
# 使用前向传播函数计算每层的激活值和加权输入
a1, z2, a2, z3, h = feed_forward(theta, X) # 前向传播,计算激活值和加权输入
# 计算输出层的误差
d3 = h - y # (5000, 10) # 计算输出层误差,预测输出与实际标签之差
# 计算第一个隐藏层的误差,忽略偏置项
d2 = d3 @ t2[:,1:] * sigmoid_gradient(z2) # (5000, 25) # 计算第一个隐藏层误差
# 计算输出层的梯度
D2 = d3.T @ a2 # (10, 26) # 计算输出层的梯度
# 计算第一个隐藏层的梯度
D1 = d2.T @ a1 # (25, 401) # 计算第一个隐藏层的梯度
# 将两个梯度矩阵序列化为一个向量
D = (1 / len(X)) * serialize(D1, D2) # (10285,) # 将梯度矩阵序列化为向量,并按样本数量平均
return D # 返回梯度向量
2.4梯度检测
在你的神经网络中,你正在最小化成本函数 J(Θ)。要对参数进行梯度检查,可以想象将参数 Θ(1)、Θ(2) "展开 "成一个长向量 θ。
假设你有一个函数 fi(θ),声称可以计算 ∂/∂θi J(θ);你想检查 fi 是否输出了正确的导数值。
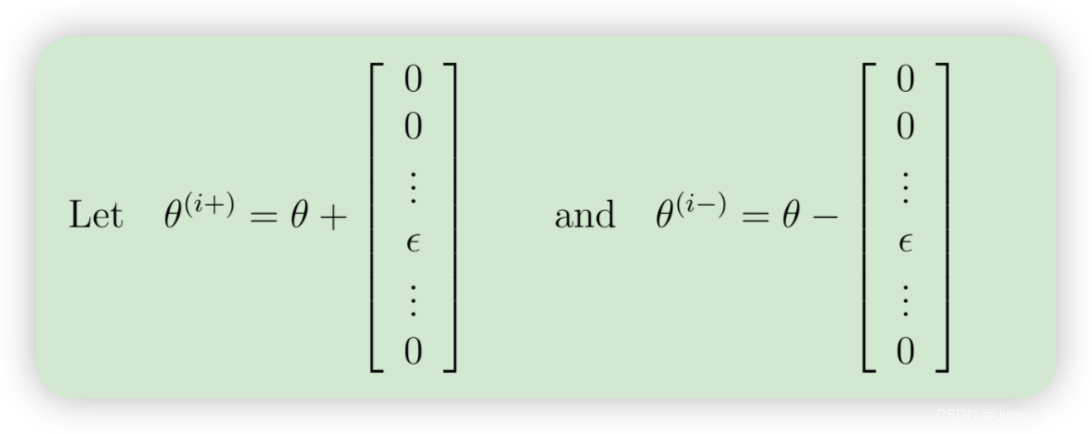
因此,θ(i+) 与 θ 相同,只是第 i 个元素增加了 。类似地,θ(i-)是第 i 个元素减少了 。现在可以用数字验证 fi(θ) 的正确性,方法是对每 i 个元素进行检验:
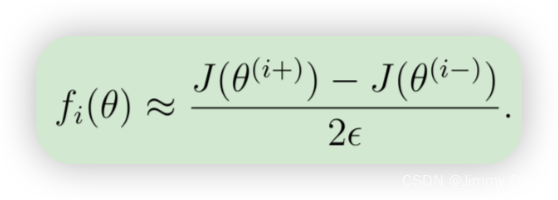
这两个值的近似程度取决于 J 的细节。不过,假设 = 10-4,你通常会发现上面左侧和右侧的值至少会相差 4 个有效数字(通常还会更多)。
我们已在 computeNumericalGradient.m 中为您实现了计算数值梯度的函数。虽然您无需修改该文件,但我们强烈建议您查看代码以了解其工作原理。在 ex4.m 的下一步,它将运行所提供的函数 checkNNGradients.m,该函数将创建一个小型神经网络和数据集,用于检查您的梯度。如果您的反向传播实现是正确的,您应该看到相对差异小于 1e-9。
def gradient_checking(theta, X, y, e):
def a_numeric_grad(plus, minus):
"""
对每个参数theta_i计算数值梯度,即理论梯度。
"""
# 计算正则化损失的数值梯度
return (regularized_cost(plus, X, y) - regularized_cost(minus, X, y)) / (e * 2)
numeric_grad = []
for i in range(len(theta)):
plus = theta.copy() # 深拷贝,否则会改变原始的theta
minus = theta.copy()
plus[i] = plus[i] + e # 在theta的第i个参数上加e
minus[i] = minus[i] - e # 在theta的第i个参数上减e
grad_i = a_numeric_grad(plus, minus) # 计算数值梯度
numeric_grad.append(grad_i) # 将计算得到的梯度添加到列表中
numeric_grad = np.array(numeric_grad) # 将梯度列表转换为NumPy数组
analytic_grad = regularized_gradient(theta, X, y) # 计算解析梯度(通过反向传播)
diff = np.linalg.norm(numeric_grad - analytic_grad) / np.linalg.norm(numeric_grad + analytic_grad) # 计算数值梯度和解析梯度的相对误差
print('If your backpropagation implementation is correct,\nthe relative difference will be smaller than 10e-9 (assume epsilon=0.0001).\nRelative Difference: {}\n'.format(diff))
2.5 正则化神经网络
成功实施反向传播算法后,您将在梯度中加入正则化。具体来说,在使用反向传播算法计算出 ∆(l) ij 后,应使用以下方法添加正则化值
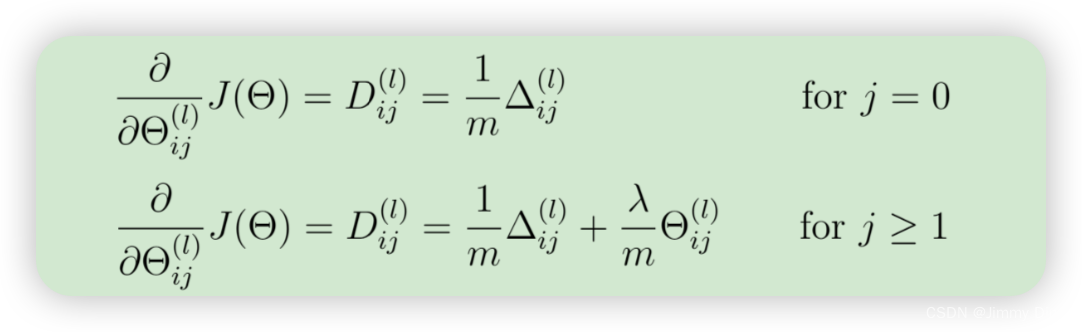
请注意,您不应对 Θ(l) 的第一列进行正则化,因为该列用于偏置项。此外,在参数 Θ(l)ij 中,i 的索引 从 1 开始,j 的索引从 0 开始
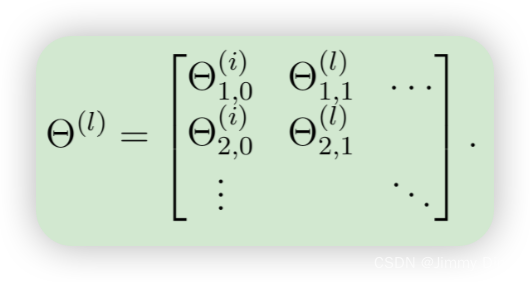
def regularized_gradient(theta, X, y, l=1):
"""不惩罚偏置单元的参数"""
# 使用 feed_forward 函数进行前向传播,计算激活值和加权输入值
a1, z2, a2, z3, h = feed_forward(theta, X)
# 使用 gradient 函数计算梯度,使用 deserialize 函数将其反序列化为 D1 和 D2
D1, D2 = deserialize(gradient(theta, X, y))
# 将 t1 和 t2 的偏置单元部分(第 0 列)设为 0,这样在正则化时不包含偏置单元的参数
t1[:,0] = 0
t2[:,0] = 0
# 计算正则化的梯度,加入正则化项,正则化参数 l 默认为 1
reg_D1 = D1 + (l / len(X)) * t1
reg_D2 = D2 + (l / len(X)) * t2
# 使用 serialize 函数将 reg_D1 和 reg_D2 序列化,并返回
return serialize(reg_D1, reg_D2)
2.6 优化参数
在成功实现神经网络代价函数和梯度计算后,ex4.m 脚本的下一步将使用 fmincg 来学习一组好的参数。训练完成后,ex4.m 脚本将通过计算正确示例的百分比来报告分类器的训练准确率。如果您的实现是正确的,那么报告的训练准确率应该在 95.3% 左右(由于随机初始化,准确率可能会有 1% 左右的变化)。通过对神经网络进行更多次的迭代训练,可以获得更高的训练精度。我们建议您尝试对神经网络进行更多迭代训练(例如,将 MaxIter 设置为 400),并改变正则化参数 λ。
def nn_training(X, y):
init_theta = random_init(10285) # 初始化权重,维度为 10285(25*401 + 10*26)
res = opt.minimize(fun=regularized_cost, # 目标函数是正则化的损失函数
x0=init_theta, # 初始权重
args=(X, y, 1), # 传递给目标函数的参数:输入数据、标签数据和正则化参数
method='TNC', # 使用信赖域牛顿共轭梯度法
jac=regularized_gradient, # 梯度函数是正则化的梯度
options={'maxiter': 400}) # 最大迭代次数为 400
return res # 返回优化结果
def accuracy(theta, X, y):
_, _, _, _, h = feed_forward(theta, X) # 进行前向传播,计算输出层激活值(预测值)
y_pred = np.argmax(h, axis=1) + 1 # 找到每行最大值的索引,表示预测的分类标签(索引加1)
print(classification_report(y, y_pred)) # 打印分类报告,包括精确度、召回率和F1-score等指标
3.可视化隐藏层
了解神经网络学习内容的一种方法是直观地观察隐藏单元捕捉到的表征。非正式地说,给定一个特定的隐藏单元,可视化其计算结果的一种方法是找到一个能使其激活的输入 x(即激活值 (a(l)i) 接近 1)。对于您训练的神经网络,请注意 Θ(1) 的第 i 行是一个 401 维的向量,代表第 i 个神经网络的参数。
隐藏单元。如果我们舍弃偏置项,就会得到一个 400 维的向量,表示从每个输入像素到隐藏单元的权重。因此,直观显示隐藏单元捕捉到的 "表示 "的一种方法是将这个 400 维向量重塑为 20 × 20 的图像并显示出来3。ex4.m 的下一步是使用 displayData 函数来实现这一功能,它将向您显示一幅包含 25 个单元的图像(与图 4 类似),每个单元对应网络中的一个隐藏单元。

def plot_hidden(theta):
t1, _ = deserialize(theta) # 反序列化 theta,得到权重矩阵 t1 和 t2(这里只关心 t1)
t1 = t1[:, 1:] # 去掉 t1 的偏置单元部分(第 0 列)
fig, ax_array = plt.subplots(5, 5, sharex=True, sharey=True, figsize=(6,6)) # 创建一个 5x5 的子图网格,图像大小为 6x6
for r in range(5): # 遍历每一行
for c in range(5): # 遍历每一列
ax_array[r, c].matshow(t1[r * 5 + c].reshape(20, 20), cmap='gray_r') # 将每个隐藏层神经元的权重可视化为 20x20 的图像
plt.xticks([]) # 去掉 x 轴刻度
plt.yticks([]) # 去掉 y 轴刻度
plt.show() # 显示图像





![适用于 Windows 11 的 5 大数据恢复软件 [免费和付费]](https://img-blog.csdnimg.cn/img_convert/7d514dfaf1bb7c2c5d07e90c2167093f.jpeg)