代码随想录-Day38

news2024/11/17 19:38:43

509. 斐波那契数

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3：

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

方法一：

class Solution {
    public int fib(int n) {
        if (n < 2) return n;
        int a = 0, b = 1, c = 0;
        for (int i = 1; i < n; i++) {
            c = a + b;
            a = b;
            b = c;
        }
        return c;
    }
}

这段代码是使用Java编写的，实现了一个计算斐波那契数列第n项的函数。斐波那契数列定义为每个数字是前两个数字之和，通常以0和1开始。这里是一个详细解析：

函数签名

public int fib(int n)

该函数名为fib，接受一个整数参数n，返回计算出的斐波那契数列的第n项。

函数逻辑

  1. 基本情况处理:

    if (n < 2) return n;

    如果n小于2（即n为0或1），直接返回n，因为斐波那契数列的前两项分别是0和1。

  2. 迭代计算斐波那契数:
    初始化三个整数变量：

    int a = 0, b = 1, c = 0;

    其中，a和b用于存储当前要相加的两个斐波那契数，初始化为0和1；c用于存储它们的和。

    接下来是一个for循环，从1遍历到n-1（因为a和b已经表示了第一项和第二项）：

    for (int i = 1; i < n; i++) {
    c = a + b;
    a = b;
    b = c;
}

    在每次循环中，先计算a和b的和赋值给c，然后将b的值赋予a，将c的值赋予b，这样a和b始终指向当前需要考虑的斐波那契数列的两项，而c则保存了新的和。

  3. 返回结果:
    循环结束后，c中存储的就是斐波那契数列的第n项，直接返回c即可。

示例

例如，如果调用fib(6)，函数会返回斐波那契数列的第6项，计算过程如下：

  • 初始：a=0, b=1, c=0
  • 第1次循环后：a=1, b=1, c=1
  • 第2次循环后：a=1, b=2, c=3
  • 第3次循环后：a=2, b=3, c=5
  • 第4次循环后：a=3, b=5, c=8
  • 第5次循环后：a=5, b=8, c=13

因此，fib(6)返回13。

方法二：

//非压缩状态的版本
class Solution {
    public int fib(int n) {
        if (n <= 1) return n;             
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for (int index = 2; index <= n; index++){
            dp[index] = dp[index - 1] + dp[index - 2];
        }
        return dp[n];
    }
}

这段代码是使用Java语言实现的一个计算斐波那契数列第n项的函数。斐波那契数列是一个经典的数列，其中每一项都是前两项的和，通常以0和1开始。下面是这段代码的详细解释：

函数签名

public int fib(int n)

这个函数名为fib，接收一个整数n作为参数，返回斐波那契数列的第n项。

函数逻辑

  1. 基本情况处理:

    if (n <= 1) return n;

    如果输入的n小于或等于1，根据斐波那契数列的定义，直接返回n自身，因为fib(0)=0且fib(1)=1。

  2. 初始化动态规划数组:

    int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;

    创建一个长度为n+1的数组dp来存储斐波那契数列的值，其中dp[0]=0和dp[1]=1对应斐波那契数列的前两项。

  3. 动态规划填充数组:

    for (int index = 2; index <= n; index++){
    dp[index] = dp[index - 1] + dp[index - 2];
}

    从索引2开始遍历到n（包含n），使用循环依次计算并存储斐波那契数列的每一项。每一项dp[index]的值由前两项dp[index - 1]和dp[index - 2]的和计算得出，这是斐波那契数列的基本定义。

  4. 返回结果:

    return dp[n];

    在循环结束后，数组dp的最后一个元素dp[n]即为斐波那契数列的第n项，所以直接返回该值。

示例

比如，如果调用fib(6)，函数会计算并返回斐波那契数列的第6项，即0, 1, 1, 2, 3, 5, 8中的8。

这种方法称为动态规划，相较于递归解法，它避免了重复计算，提高了效率，特别是在计算较大的n时更为明显。

70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

  1. 1 阶 + 1 阶
  2. 2 阶
    示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

  1. 1 阶 + 1 阶 + 1 阶
  2. 1 阶 + 2 阶
  3. 2 阶 + 1 阶
    在这里插入图片描述

方法一：

// 常规方式
public int climbStairs(int n) {
    int[] dp = new int[n + 1];
    dp[0] = 1;
    dp[1] = 1;
    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}

这段代码是使用Java语言实现的一种动态规划方法，用于解决“爬楼梯”问题。问题描述如下：假设你正在爬一个楼梯，每次你可以爬1阶或者2阶。给定楼梯的总阶数n，返回爬到楼顶的方法总数。

代码解析

  • 初始化: 创建一个长度为n + 1的整型数组dp，用来存储爬到各个阶梯的方法数。dp[0]和dp[1]都初始化为1，表示爬到第0阶有1种方法（即不爬），爬到第1阶也有1种方法（直接爬一阶上去）。

  • 状态转移方程: 对于dp[i]（其中i >= 2），可以根据状态转移方程dp[i] = dp[i - 1] + dp[i - 2]来计算，即爬到第i阶的方法数等于爬到第i - 1阶的方法数加上爬到第i - 2阶的方法数。这是因为到达第i阶，要么是从第i - 1阶爬一阶上来，要么是从第i - 2阶爬两阶上来。

  • 返回结果: 最终，dp[n]就是爬到第n阶楼梯的方法总数，因此返回dp[n]作为答案。

举例说明

假设n = 3，即有3阶楼梯，按照代码逻辑计算过程如下：

  • dp[0] = 1, dp[1] = 1
  • 计算dp[2]时，dp[2] = dp[1] + dp[0] = 1 + 1 = 2，表示到第2阶有2种方法（1+1 或者 2）。
  • 计算dp[3]时，dp[3] = dp[2] + dp[1] = 2 + 1 = 3，表示到第3阶有3种方法（1+1+1, 1+2, 或者 2+1）。

因此，当n = 3时，返回的结果是3，即有3种不同的方法爬到楼顶。

方法二：

// 用变量记录代替数组
class Solution {
    public int climbStairs(int n) {
        if(n <= 2) return n;
        int a = 1, b = 2, sum = 0;

        for(int i = 3; i <= n; i++){
            sum = a + b;  // f(i - 1) + f(i - 2)
            a = b;        // 记录f(i - 1)，即下一轮的f(i - 2)
            b = sum;      // 记录f(i)，即下一轮的f(i - 1)
        }
        return b;
    }
}

这段代码是使用Java语言实现的一个简化版的动态规划方法来解决“爬楼梯”问题。与之前使用数组记录每个阶梯的方法数不同，这里仅使用了三个变量a、b和sum来减少空间复杂度，达到了O(1)的空间复杂度要求，而时间复杂度仍然是O(n)。下面是代码的详细解释：

代码逻辑解析

  • 基础情况处理: 如果输入的阶数n小于等于2，直接返回n，因为当只有1阶或2阶楼梯时，方法数分别为1和2。

  • 变量初始化: 定义三个整型变量a、b和sum，其中a和b分别初始化为1和2，对应爬到第一阶和第二阶楼梯的方法数。sum用来临时存储每轮循环中爬到当前阶的方法数。

  • 循环计算: 从第三阶楼梯(i = 3)开始计算，直到目标阶数n。在每次循环中：

    • 计算sum = a + b，即当前阶的方法数等于前一阶的方法数加上前两阶的方法数。
    • 更新a = b，把当前的b值（即上一阶的方法数）赋给a，为下一轮计算做准备。
    • 更新b = sum，把刚计算出来的sum（当前阶的方法数）赋给b，为下一轮计算做准备。

  • 返回结果: 循环结束后，变量b中存储的就是爬到n阶楼梯的方法总数，直接返回b。

举例说明

假设我们要计算爬5阶楼梯的方法数，过程如下：

  1. 初始：a = 1（到第1阶的方法数），b = 2（到第2阶的方法数）。
  2. 第一轮计算（阶数3）: sum = a + b = 1 + 2 = 3，更新后a = 2, b = 3。
  3. 第二轮计算（阶数4）: sum = a + b = 2 + 3 = 5，更新后a = 3, b = 5。
  4. 第三轮计算（阶数5）: sum = a + b = 3 + 5 = 8，此时b即为爬到第5阶的方法数。

最终返回b = 8，表示有8种不同的方法可以爬到5阶楼梯的顶部。

746. 使用最小花费爬楼梯

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。

  • 支付 15 ，向上爬两个台阶，到达楼梯顶部。
    总花费为 15 。
    示例 2：

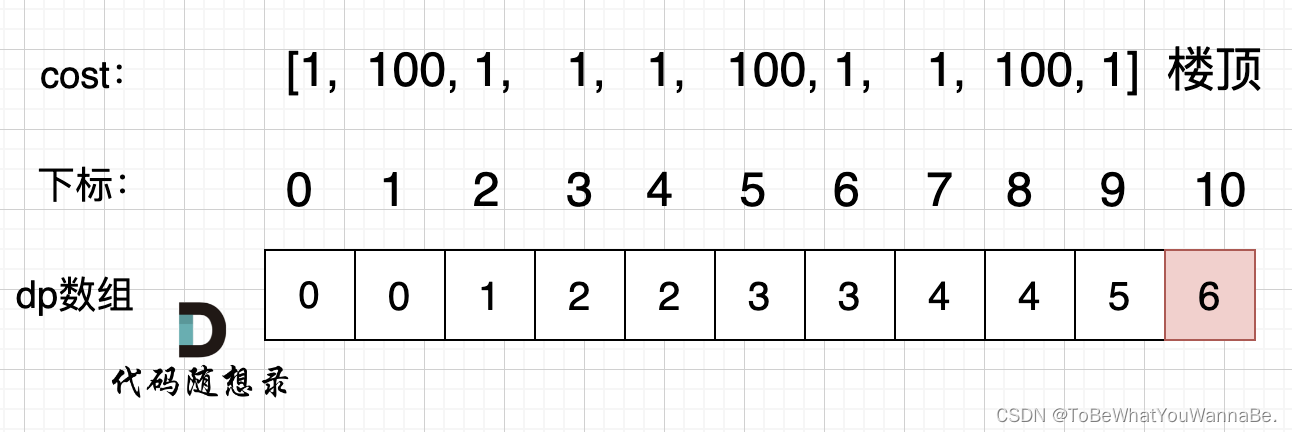
输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。

  • 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
  • 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
  • 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
  • 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
  • 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
  • 支付 1 ，向上爬一个台阶，到达楼梯顶部。
    总花费为 6 。
    在这里插入图片描述

方法一：

// 方式一：第一步不支付费用
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int len = cost.length;
        int[] dp = new int[len + 1];

        // 从下标为 0 或下标为 1 的台阶开始，因此支付费用为0
        dp[0] = 0;
        dp[1] = 0;

        // 计算到达每一层台阶的最小费用
        for (int i = 2; i <= len; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }

        return dp[len];
    }
}

这段Java代码是解决“最小成本爬楼梯”问题的一个实现。给定一个非负整数数组 cost，其中 cost[i] 是爬到第 i 阶楼梯的成本。一旦你支付了爬到某阶楼梯的成本，就可以选择不再支付直接爬到更高一层或者爬两层。该函数的目标是计算达到顶层楼梯的最低花费。这里采用的是自底向上的动态规划方法。

代码解析：

  1. 初始化：首先，定义数组 dp 来存储到达每个楼层的最小成本，数组长度为 len + 1，因为我们要计算到达最后一阶楼梯之上（即到达顶层）的成本。初始化 dp[0] 和 dp[1] 为0，意味着从地面（下标0）或第一个台阶（下标1）开始爬，不需要额外支付费用。

  2. 动态规划状态转移：遍历从下标2到len（包括len），对于每个位置 i，有两种方式到达：一是从 i-1 阶楼梯爬上来，二是从 i-2 阶楼梯爬上来。因此，到达第 i 阶楼梯的最小成本可以通过比较这两种方式的成本并取最小值得到，即 dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])。

  3. 返回结果：遍历结束后，dp[len] 存储的就是到达顶层楼梯的最小成本，直接返回这个值。

示例说明：

假设 cost = [10, 15, 20]，表示爬到第一阶楼梯成本为0（根据初始化逻辑），第二阶为10，第三阶为15。按照上述逻辑计算：

  • dp[2] = min(dp[1] + cost[1], dp[0] + cost[0]) = min(0 + 10, 0 + 0) = 10
  • dp[3] = min(dp[2] + cost[2], dp[1] + cost[1]) = min(10 + 20, 0 + 15) = 15

因此，到达顶层（即第三阶楼梯之上）的最小成本为15，这就是函数的返回值。

方法二：

// 方式二：第一步支付费用
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int[] dp = new int[cost.length];
        dp[0] = cost[0];
        dp[1] = cost[1];
        for (int i = 2; i < cost.length; i++) {
            dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
        }
        //最后一步，如果是由倒数第二步爬，则最后一步的体力花费可以不用算
        return Math.min(dp[cost.length - 1], dp[cost.length - 2]);
    }
}

这段Java代码也是解决“最小成本爬楼梯”问题的一个实现，但与之前的方式稍有不同。这里是假设从第一阶楼梯开始就需要支付费用，然后采用动态规划的方法来求解到达顶层楼梯的最小花费。具体解析如下：

代码解析：

  1. 初始化：首先，定义一个长度与输入数组 cost 相同的数组 dp，用来存储到达每个阶梯时的最小花费。初始化 dp[0] 和 dp[1] 分别为 cost[0] 和 cost[1]，表示从地面到第一阶和到第二阶的花费。

  2. 动态规划状态转移：从下标为2的位置开始遍历至数组末尾（不包括），对于每一个位置 i，到达此处的最小花费等于前一阶梯的最小花费和前前一阶梯的最小花费中的较小者，再加上当前位置 i 的花费。即 dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i]。这样做是为了确保以最少的花费到达当前阶梯。

  3. 返回结果：到达顶层楼梯有两种情况，一种是从倒数第一阶直接上，一种是从倒数第二阶上。因此，返回 dp[cost.length - 1] 和 dp[cost.length - 2] 中的较小值，即为最小成本。注意，这里最后一步不额外计算费用，因为到达倒数第二阶时，已经计算了到达顶层所需的最小花费。

示例说明：

如果 cost = [10, 15, 20]，则：

  • dp[0] = 10
  • dp[1] = 15
  • 遍历过程中，dp[2] = min(dp[1], dp[0]) + cost[2] = min(15, 10) + 20 = 10 + 20 = 30

最后，Math.min(dp[2], dp[1]) = Math.min(30, 15)，因此返回 15 作为最小成本。

这种方式同样高效地解决了问题，但注意其假设前提与之前的方式不同，是从第一阶开始就需要支付费用。

方法三：

// 状态压缩，使用三个变量来代替数组
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        // 以下三个变量分别表示前两个台阶的最少费用、前一个的、当前的。
        int beforeTwoCost = 0, beforeOneCost = 0, currentCost = 0;
        // 前两个台阶不需要费用就能上到，因此从下标2开始；因为最后一个台阶需要跨越，所以需要遍历到cost.length
        for (int i = 2; i <= cost.length; i ++) {
            // 此处遍历的是cost[i - 1]，不会越界
            currentCost = Math.min(beforeOneCost + cost[i - 1], beforeTwoCost + cost[i - 2]);
            beforeTwoCost = beforeOneCost;
            beforeOneCost = currentCost;
        }
        return currentCost;
    }
}

这段Java代码是解决“最小成本爬楼梯”问题的另一种实现，采用了状态压缩的方法，即使用三个变量而不是数组来存储到达每个阶梯所需的最小成本。这种方式减少了空间复杂度，但仍然保持了动态规划的思想。下面是详细的解析：

代码解析：

  1. 变量定义：定义三个整型变量beforeTwoCost、beforeOneCost和currentCost，分别代表到达前两个台阶、前一个台阶和当前台阶的最小成本。初始时，前两个台阶和前一个台阶的最小成本都设为0，因为题目中并没有明确指出从第一个台阶开始就有费用，但根据逻辑推断，此处默认从地面到第一个和第二个台阶是免费的，或者理解为beforeTwoCost和beforeOneCost是站在第一阶和第二阶的费用，自然为0。

  2. 循环遍历：从i = 2开始遍历至cost.length（包含cost.length，意味着考虑到达顶层楼梯后的状态），这一步是基于从地面（下标0）或第一个台阶（下标1）出发的逻辑，但因为cost数组的下标是从0开始的，所以计算时访问的是cost[i - 1]和cost[i - 2]。

  3. 状态转移：在每次循环中，计算到达当前台阶的最小成本currentCost，通过比较从上一个台阶和前一个台阶到达当前台阶的最小花费。具体来说，currentCost = Math.min(beforeOneCost + cost[i - 1], beforeTwoCost + cost[i - 2])，表示当前到达的阶梯可以通过上一个阶梯或跳过一个阶梯从更早的阶梯到达，选择其中成本较小的路径。

  4. 状态更新：更新beforeTwoCost和beforeOneCost的值，为下一次迭代做准备。即将当前的beforeOneCost赋值给beforeTwoCost，将刚刚计算的currentCost赋值给beforeOneCost。

  5. 返回结果：循环结束后，currentCost即为到达顶层楼梯所需的最小成本，直接返回。

示例说明：

如果输入数组cost = [10, 15, 20]，则遍历过程如下：

  • 初始化：beforeTwoCost = 0, beforeOneCost = 0
  • 第一轮计算（i = 2）：currentCost = min(0 + 10, 0 + 0) = 10，更新后beforeTwoCost = 0, beforeOneCost = 10
  • 第二轮计算（i = 3）：currentCost = min(10 + 15, 0 + 20) = 20，更新后beforeTwoCost = 10, beforeOneCost = 20

遍历结束，currentCost = 20即为最小成本，因此返回20。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1858904.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Android】我的手机在...自己下载...那个（浅析Intent基础运用）

【Android】我的手机在...自己下载...那个（浅析Intent基础运用）

【Android】我的手机在…自己下载…那个&#xff08;浅析Intent基础运用&#xff09; 在Android开发中&#xff0c;Intent&#xff08;意图&#xff09;是一个非常重要的概念。它不仅仅是用于在应用程序的各个组件之间进行通信的工具&#xff0c;也是启动新的Activity、Servic…
阅读更多...
FydeOS导入VMware虚拟机之后，如何扩展系统硬盘大小？

FydeOS导入VMware虚拟机之后，如何扩展系统硬盘大小？

前言​ 最近查询FydeOS系统的小伙伴不在少数啊&#xff01;可见这个系统是相当nice的&#xff0c;小伙伴们都是尝试尝试。 看到有不少小伙伴通过VMware虚拟机使用FydeOS&#xff0c;那么你就肯定知道官方包导入VMware之后&#xff0c;硬盘只显示分区了20GB。 如果这时候使用Fy…
阅读更多...
【Java核心技术13】Java中的构造器与析构器：深入解析与代码示例

【Java核心技术13】Java中的构造器与析构器：深入解析与代码示例

引言 所有文章均为原创验证&#xff0c;您随手的 关注、点赞、收藏 是我创作最大的动力。 示例代码地址&#xff1a;https://gitee.com/code-in-java/csdn-blog.git 在面向对象编程语言中&#xff0c;构造器和析构器是类生命周期管理的关键部分。构造器负责初始化新创建的对象&…
阅读更多...
Java NIO（一） 概述

Java NIO（一） 概述

NIO主要用于以少量线程来管理多个网络连接&#xff0c;处理其上的读写等事件。在大量连接情况下&#xff0c;不管是效率还是空间占用都要优于传统的BIO。 Java NIO 由以下几个核心部分组成&#xff1a; Channel Buffer Selector Selector 如果你的应用打开了多个连接&#x…
阅读更多...
Hack The Box-Axlle【更新中】

Hack The Box-Axlle【更新中】

总体思路 XLL-EXEC->hta反弹shell->重置用户密码->重写二进制文件 信息收集&端口利用 nmap -sSVC axlle.htb开放了一大堆端口&#xff0c;这里先挑重点的80端口和445端口查看 80端口主页只有一个邮箱账号&#xff0c;对其目录扫描和子域名扫描 dirsearch -u h…
阅读更多...
Python统计实战：3D散点图绘制

Python统计实战：3D散点图绘制

为了解决特定问题而进行的学习是提高效率的最佳途径。这种方法能够使我们专注于最相关的知识和技能&#xff0c;从而更快地掌握解决问题所需的能力。 &#xff08;以下练习题来源于《统计学—基于Python》。联系获取完整数据和Python源代码文件。&#xff09; 练习题 用以下数…
阅读更多...
【力扣】从前序与中序遍历序列构造二叉树

【力扣】从前序与中序遍历序列构造二叉树

&#x1f525;博客主页&#xff1a; 我要成为C领域大神 &#x1f3a5;系列专栏&#xff1a;【C核心编程】 【计算机网络】 【Linux编程】 【操作系统】 ❤️感谢大家点赞&#x1f44d;收藏⭐评论✍️ 本博客致力于分享知识&#xff0c;欢迎大家共同学习和交流。 给定两个整数数…
阅读更多...
测评：【ONLYOFFICE】版本更迭与AI加持下的最新ONLYOFFICE桌面编辑器8.1

测评：【ONLYOFFICE】版本更迭与AI加持下的最新ONLYOFFICE桌面编辑器8.1

你是否还在为没有一款合适的在线桌面编辑器而苦恼&#xff1f;你是否还在因为办公软件的选择过少而只能使用WPS或者office&#xff1f;随着办公需求的不断变化和发展&#xff0c;办公软件也在不断更新和改进。ONLYOFFICE 作为一款全功能办公软件&#xff0c;一直致力于为用户提…
阅读更多...
视图(views)

视图(views)

自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 下面通过一个例子讲解在Django项目中定义视图&#xff0c;代码如下&#xff1a; from django.http import HttpResponse # 导入响应对象 impo…
阅读更多...
android-aidl4

android-aidl4

转&#xff1a;Android Aidl的使用_android aidl使用-CSDN博客 一.准备 Parcelable&#xff0c;可以理解成只是把car整个对象在aidl中进行传递&#xff0c;就理解成一个car的一个类吧&#xff0c;和其他类使用一样就行了&#xff0c;回调&#xff1a;把接口作为参数放在函数参…
阅读更多...
Mysql: SQL-DDL

Mysql: SQL-DDL

一.SQL通用语法 1.SQL可以单行或者多行书写,以分号结尾。 2.SQL语句可以使用空格/缩进来增强语句的可读性。 3.MySQL数据库的SQL语句不区分大小写,关键字建议用大写。 4.注释: 单行注释:注释内容或#注释内容(Mysql特有) 多行注释&#xff1a;/*注释内容*/ 二.SQL分类 1.D…
阅读更多...
常用MQ消息中间件Kafka、ZeroMQ和RabbitMQ对比及RabbitMQ详解

常用MQ消息中间件Kafka、ZeroMQ和RabbitMQ对比及RabbitMQ详解

1、概述 在现代的分布式系统和实时数据处理领域&#xff0c;消息中间件扮演着关键的角色&#xff0c;用于解决应用程序之间的通信和数据传递的挑战。在众多的消息中间件解决方案中&#xff0c;Kafka、ZeroMQ和RabbitMQ 是备受关注和广泛应用的代表性系统。它们各自具有独特的特…
阅读更多...
Msql----表的约束

Msql----表的约束

提示&#xff1a;以下是本篇文章正文内容&#xff0c;下面案例可供参考 一、表的约束 表的约束&#xff1a;表中一定要有约束&#xff0c;通过约束让插入表中的数据是符合预期的。它的本质是通过技术手段&#xff0c;让程序员插入正确的数据&#xff0c;约束的最终目标是保证…
阅读更多...
AVL树插入详解

AVL树插入详解

1.什么是AVL树 二叉搜索树可以提高搜索的效率&#xff0c;但是如果数据有序或者接近有序&#xff0c;就会退化为单边树&#xff0c;查找效率相当于在顺序表中查找数据&#xff0c;时间复杂度会退化到O(n)。AVL树解决了这个问题&#xff0c;通过保证每个节点的左右子树高度之差…
阅读更多...
BoosterX：专为游戏爱好者打造的终极 Windows 系统优化工具

BoosterX：专为游戏爱好者打造的终极 Windows 系统优化工具

《黑神话&#xff1a;悟空》、《艾尔登法环&#xff1a;黄金树幽影》、暴雪「全家桶」回归……下半年&#xff0c;我们将迎来一场豪华的游戏大餐&#xff01; 想要畅玩游戏&#xff0c;除了要准备好给力的硬件设备&#xff0c;系统优化当然也不能落下&#xff01; BoosterX 正…
阅读更多...
C++在VS2022开发Windows窗口程序1:第一个win窗口程序

C++在VS2022开发Windows窗口程序1:第一个win窗口程序

Windows操作系统是由微软公司开发和维护的一系列图形化操作系统的统称。Windows操作系统主要用于个人计算机、笔记本电脑、平板电脑、服务器等设备上。Windows起源于Microsoft-DOS模拟环境&#xff0c;相比于DOS的指令化模式&#xff0c;Windows采用图形化的模式&#xff0c;因…
阅读更多...
微信小程序 引入MiniProgram Design失败

微信小程序 引入MiniProgram Design失败

这tm MiniProgramDesign 是我用过最垃圾的框架没有之一 我按照官网的指示安装居然能安装不成功,牛! 这里说明我是用js开发的 到以上步骤没有报错什么都没有,然后在引入组件的时候报错 Component is not found in path “./miniprogram _npm/vant/weapp/button/index” (using…
阅读更多...
SAPUI5基础知识9 - JSON Module与数据绑定

SAPUI5基础知识9 - JSON Module与数据绑定

1. 背景 在前面的博客中&#xff0c;我们已经学习了SAPUI5中视图和控制器的使用&#xff0c;在本篇博客中&#xff0c;让我们学习下MVC架构中的M-模型了。 SAPUI5中的JSON Model是一个客户端模型&#xff0c;可以用于在SAPUI5应用程序中处理和操作JSON数据。SAPUI5提供了绑定…
阅读更多...
prometheus+grafana搭建监控系统

prometheus+grafana搭建监控系统

1.prometheus服务端安装 1.1下载包 使用wget下载 &#xff08;也可以直接去官网下载包Download | Prometheus&#xff09; wget https://github.com/prometheus/prometheus/releases/download/v2.44.0/prometheus-2.44.0.linux-amd64.tar.gz1.2解压 tar xf prometheus-2.44…
阅读更多...
Flutter ffi Failed to lookup symbol

Flutter ffi Failed to lookup symbol

iOS release版本&#xff0c;解决方式参考官方文档&#xff1a;在 iOS 中使用 dart:ffi 调用本地代码 如果debug版本也报这个错误&#xff0c;很可能是有多个.c文件&#xff0c;编译的时候没带上&#xff01; 假设你的ffi模块名字是 c_lib 对于Android端&#xff0c;需要修改…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023