1.什么是AVL树
二叉搜索树可以提高搜索的效率,但是如果数据有序或者接近有序,就会退化为单边树,查找效率相当于在顺序表中查找数据,时间复杂度会退化到O(n)。AVL树解决了这个问题,通过保证每个节点的左右子树高度之差的绝对值不超过1,将时间复杂度保证在O(log2(n))左右。

2.AVL树的结构
- 创建指针分别指向左孩子,右孩子和父亲节点
- 创建平衡因子_bf,平衡因子就是右子树高度减左子树高度
- 创建Pair存键值对
template<class K, class V>
struct AVLTreeNode
{
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
int _bf;
pair<K, V> _kv;
AVLTreeNode(const pair<K, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _bf(0)
, _kv(kv)
{}
}3.AVL树的插入
-
按二叉搜索树的规则插入
-
更新平衡因子
- 根据平衡因子,改变树的结构
在寻找插入位置时,需要记录父亲节点的指针,通过判断需要插入的键和父亲节点的键的大小,找到插入节点在父亲节点的左右,进而更新一下树的平衡因子,最后根据平衡因子进行树结构的调节
- 向树中插入一个节点,这个节点只会影响它的祖先,不影响其他节点。所以我们在插入节点的祖先节点中更新平衡因子
- 如果parent的平衡因子=0,说明parent原来的平衡因子绝对值=1,新插入节点在父节点的空孩子,不会影响祖先节点,直接返回即可

- 如果parent的平衡因子的绝对值为1,需要向上更新祖先节点的平衡因子
- 下面的情况从新增节点,向上更新发生的
- 如果parent的平衡因子=2,cur的平衡因子=1,进行左单旋
- 如果parent的平衡因子=2,cur的平衡因子=-1,进行左右单旋
- 如果parent的平衡因子=-2,cur的平衡因子=-1,进行右单旋
- 如果parent的平衡因子=-2,cur的平衡因子=1,进行左右单旋
template<class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
while (parent)
{
if(cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
cur = cur->_parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
// 旋转处理
if (parent->_bf == 2 && cur->_bf == 1)
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1)
{
RotateR(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
else
{
RotateRL(parent);
}
break;
}
else
{
// 插入之前AVL树就有问题
assert(false);
}
}
return true;
}4.旋转调整
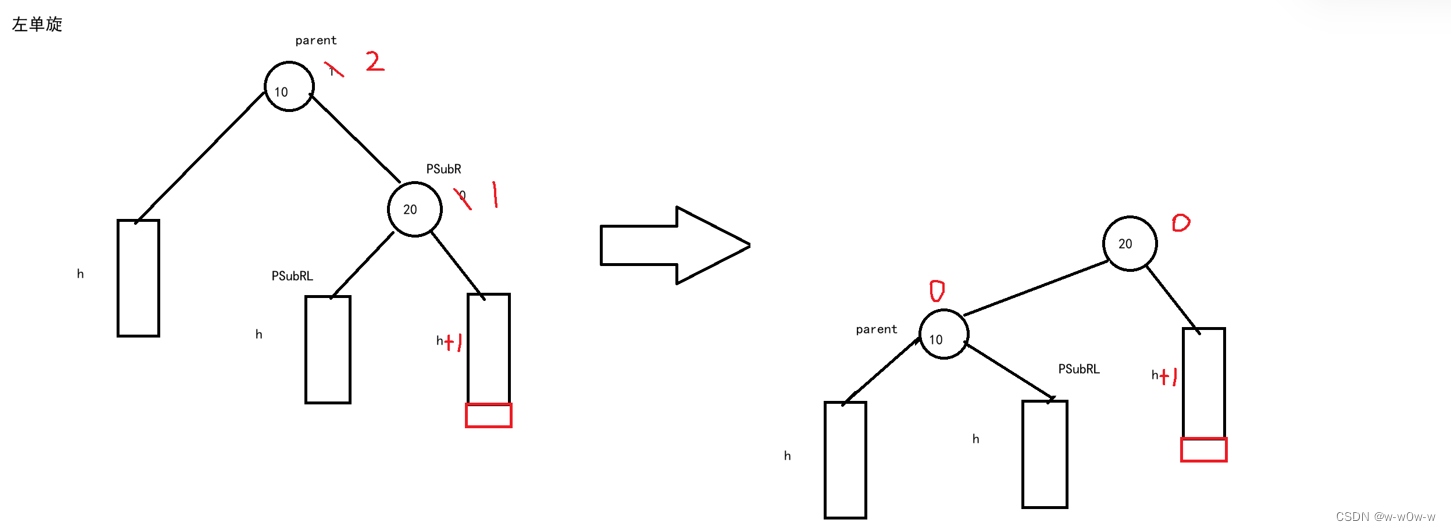
1.左单旋
- 触发条件:当某个节点的右子树高度比左子树高度高出2时(即平衡因子为2),且子节点的右子树高度比左子树高1时(即平衡因子为1),需要进行左单旋来重新平衡树。
- 旋转点:parent为触发旋转的节点(平衡因子=2),SubR为parent的右孩子,SubRL为SubR的左孩子
- 旋转过程:把SubRL变成parent的右孩子,把parent变成SubR的左孩子,把原parent的父亲节点变成SubR的父亲节点
- 更新平衡因子:SubR的平衡因子=0,parent的平衡因子=0
- 重复操作:递归向上调整
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if(subRL)
subRL->_parent = parent;
subR->_left = parent;
Node* ppnode = parent->_parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subR;
}
else
{
ppnode->_right = subR;
}
subR->_parent = ppnode;
}
parent->_bf = 0;
subR->_bf = 0;
}
2.右单旋
- 触发条件:当某个节点的左子树高度比右子树高度高出2时(即平衡因子为2),且子节点的左子树高度比右子树高1时(即平衡因子为-1),需要进行左单旋来重新平衡树。
- 旋转点:parent为触发旋转的节点(平衡因子=-2),SubL为parent的左孩子,SubLR为SubR的右孩子
- 旋转过程:把SubLR变成parent的左孩子,把parent变成SubL的右孩子,把原parent的父亲节点变成SubL的父亲节点
- 更新平衡因子:SubR的平衡因子=0,parent的平衡因子=0
- 重复操作:递归向上调整

void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
subL->_right = parent;
Node* ppnode = parent->_parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subL;
}
else
{
ppnode->_right = subL;
}
subL->_parent = ppnode;
}
subL->_bf = 0;
parent->_bf = 0;
}3.右左单旋
- 触发条件:当某个节点的右子树高度比左子树高度高出2时(即平衡因子为2),且子节点的左子树高度比右子树高1时(即平衡因子为-1),需要进行左单旋来重新平衡树。
- 旋转点:parent为触发旋转的节点(平衡因子=2),SubR为parent的右孩子,SubRL为SubR的左孩子
- 旋转过程:将SubR进行右单旋,再对parent进行左单旋
- 更新平衡因子:根据SubRL原平衡因子,更新SubR和parent的平衡因子
- 重复操作:递归向上调整



void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(subR);
RotateL(parent);
subRL->_bf = 0;
if (bf == 1)
{
subR->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1)
{
parent->_bf = 0;
subR->_bf = 1;
}
else
{
parent->_bf = 0;
subR->_bf = 0;
}
}
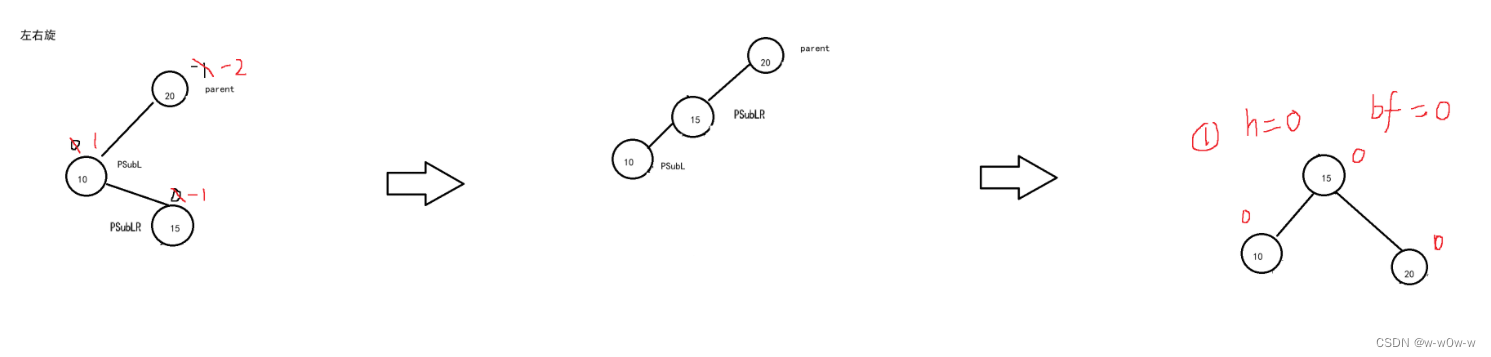
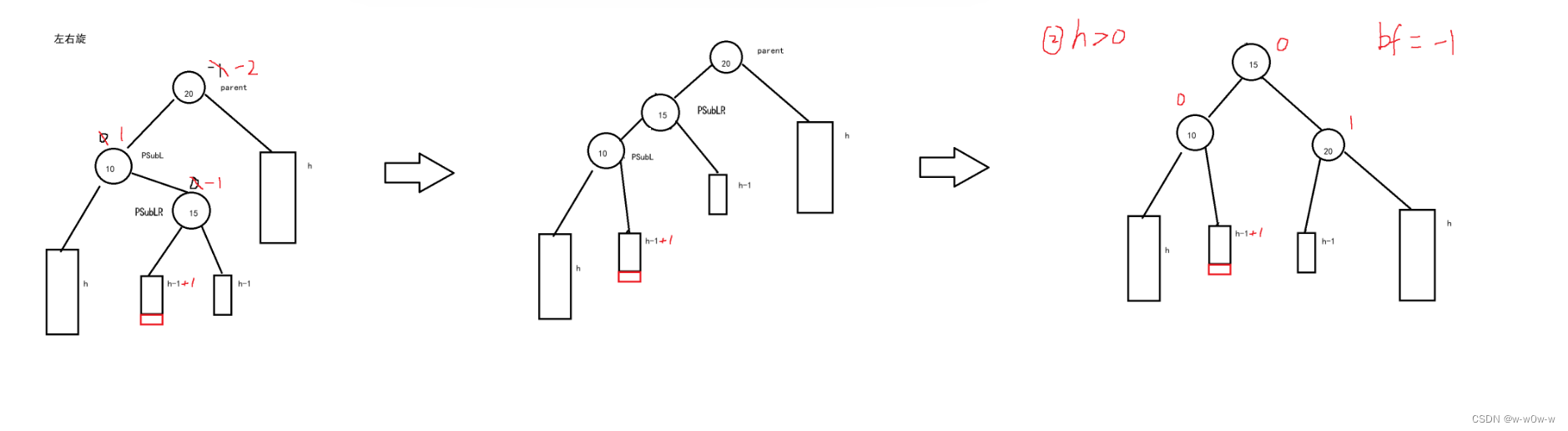
4.左右单旋
- 触发条件:当某个节点的左子树高度比右子树高度高出2时(即平衡因子为-2),且子节点的右子树高度比左子树高1时(即平衡因子为1),需要进行左单旋来重新平衡树。
- 旋转点:parent为触发旋转的节点(平衡因子=2),SubL为parent的左孩子,SubLR为SubR的右孩子
- 旋转过程:将SubL进行左单旋,再对parent进行右单旋
- 更新平衡因子:根据SubLR原平衡因子,更新SubL和parent的平衡因子
- 重复操作:递归向上调整

void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == -1)
{
subLR->_bf = 0;
subL->_bf = 0;
parent->_bf = 1;
}
else if (bf == 1)
{
subLR->_bf = 0;
subL->_bf = -1;
parent->_bf = 0;
}
else if (bf == 0)
{
subLR->_bf = 0;
subL->_bf = 0;
parent->_bf = 0;
}
else
{
assert(false);
}
}