Mysql索引底层数据结构
1、什么是索引
索引在项目中还是比较常见的,它是帮助MySQL高效获取数据的数据结构,主要是用来提高数据检索的效率,降低数据库的IO成本,同时通过索引列对数据进行排序,降低数据排序的成本,也能降低了CPU的消耗
2、索引的优缺点
索引的优点:
- 提高数据库检索效率,降低数据库 IO 成本
- 可以通过索引对数据进行排序,减少排序成本
缺点: - 占用磁盘空间
- 对于写多查少的数据,不适合加索引。
3、红黑树和二叉树
我们都知道 Mysql 的 InnoDB 的索引使用的是 B+树,但是为什么使用 B+树呢。我们先了解一下二叉树和红黑树这两种的数据结构。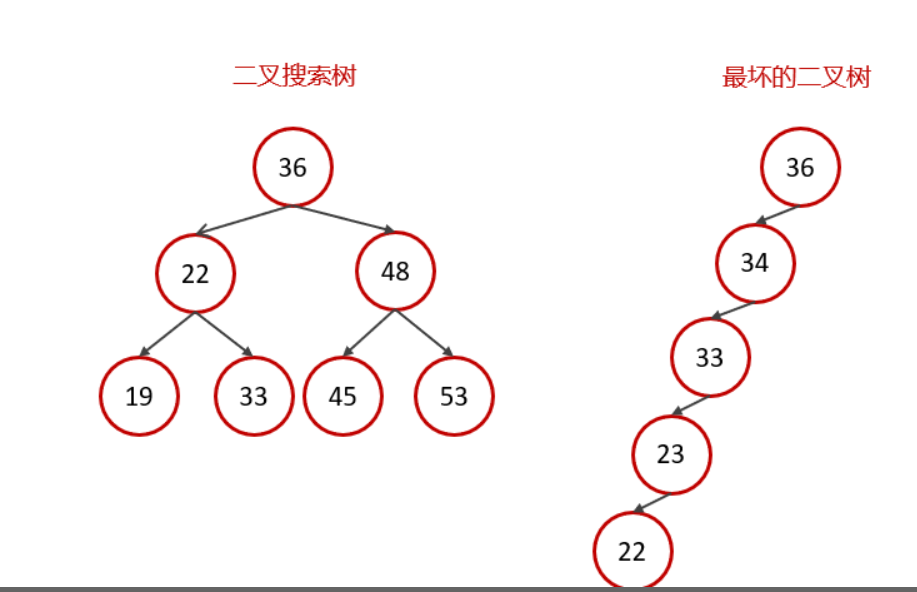
首先二叉树来说,如果在理想状态下,也就是完全二叉树的状态下,我们查找一个数据的时间复杂度是 O(logN)。
但是如果像上图一样,二叉树的数据出现了偏移,也就是树的退化现象。
当我们构建二叉树的时候插入的是有序的数据,那么就会出现树的退化。
直接后果就是,该二叉树变成了链表,查询一个数据的时间复杂度变成了 O(N),那么索引就起不到我们设计之初想让他起到的作用了(增快查询速度)。
为了解决上述的问题,有一种数据结构也就是红黑树,通过节点之间的旋转,避免了树的退化现象。
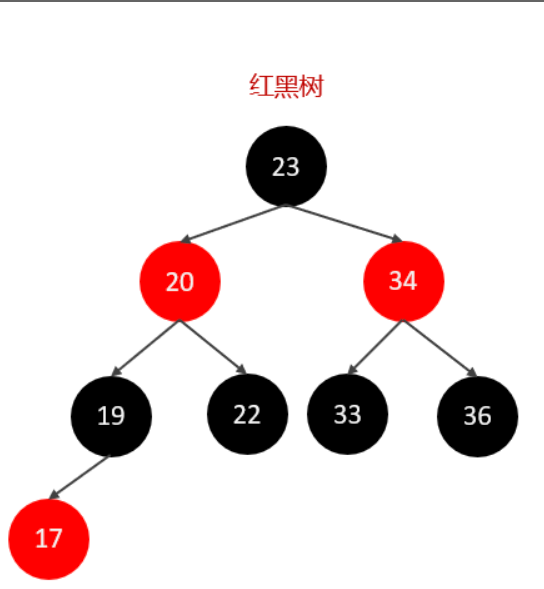
红黑树的性质: 红黑树是一棵二叉搜索树,它在每个节点增加了一个存储位记录节点的颜色,可以是 RED, 也可以是 BLACK;通过任意一条从根到叶子简单路径上颜色的约束,红黑树保证最长路径不超过最短路径的二倍,因而近似平衡。
当红黑树发生节点偏移的时候通过旋转来保证树的平衡。
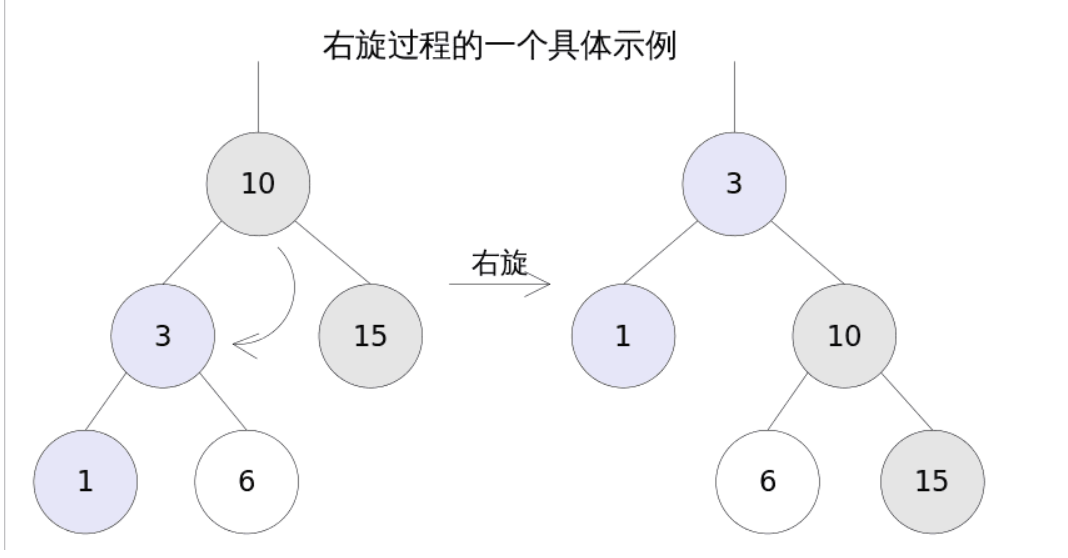
但是,对于红黑树来讲如果我们的数据比较多的情况下,那么查询数据还是 O(logN)还是跟树的高度有关。我们需要尽可能的降低树的高度。
4、B 树
B 树是一种多叉路衡查找树。
我们假定一个 B 树的度为 5,那也就是说这棵树的节点最大可以容纳四个数据,五个指针。
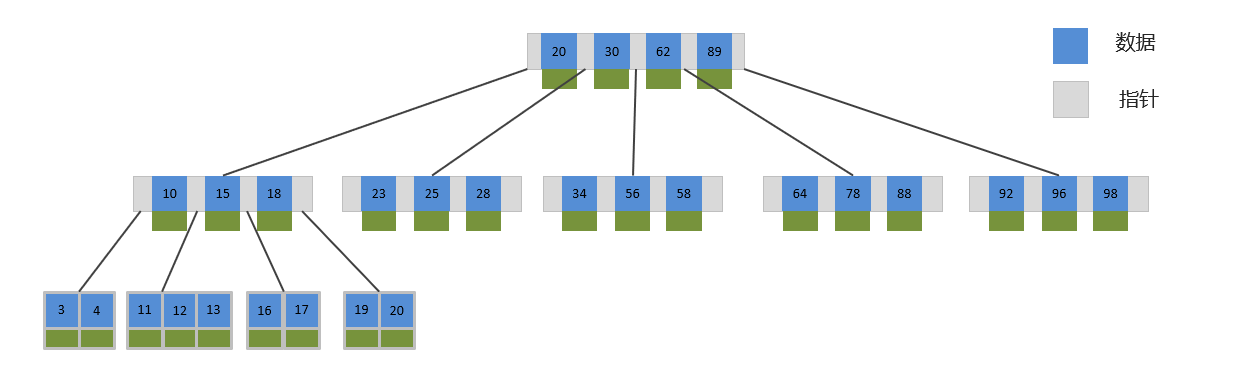
这样就可以解决树的高度过高的问题,但是 B 树的每个节点上面都有数据,这对于我们排序和查找不是那么方便,那有没有更好的数据结构呢?
5、B + 树
B+Tree 是在 BTree 基础上的一种优化,使其更适合实现外存储索引结构。
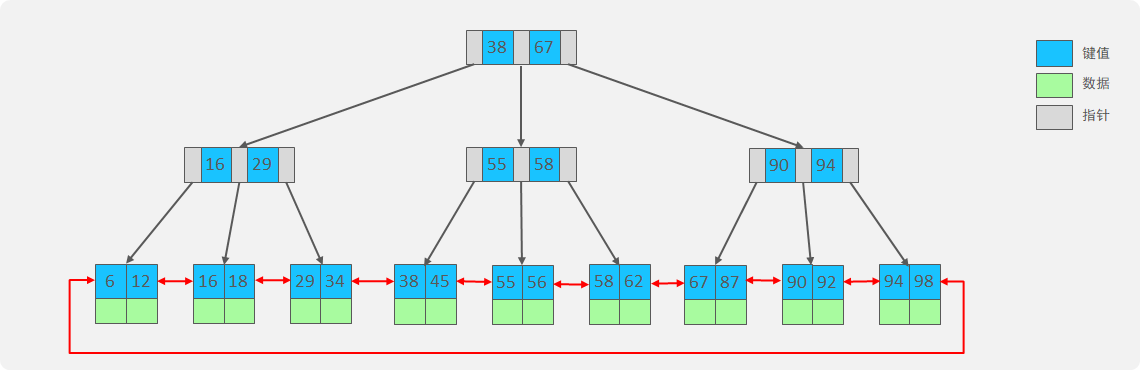
B+树的特点:在 B 树的基础上修改了以下几点:1、B+树只有叶子节点才储存数据。2、B+树的叶子节点带有指针组成一个双向循环的链表。
B 树和 B+树的区别
1、在 B 树中,非叶子节点和叶子节点都会存放数据,而 B+树的所有的数据都会出现在叶子节点,在查询的时候,B+树查找效率更加稳定
2、在进行范围查询的时候,B+树效率更高,因为 B+树都在叶子节点存储,并且叶子节点是一个双向链表
6、Hash 索引:
原理:在底层维护一张哈希表,通过哈希算法将键值算成hash值,映射到相应的槽位,存储在哈希表
特点:
- Hash索引只能用于对等的比较,不支持范围查询
- 无法利用索引完成排序操作
- 查询效率高只用进行一次检索就可以,效率通常要比B+树高
注意: 只有 Memory 存储引擎具有 Hash 索引
InnoDB 具有自适应 Hash 索引,会根据 B+树索引自动构造 Hash 索引
7、为什么 InnoDB 选择使用 B+树?
- 相对于二叉树,层级更少,搜索效率高;
- 对于 B-tree,无论是叶子节点还是非叶子节点,都会保存数据,这样导致一页中存储的键值减少,指针跟着减少,要同样保存大量数据,只能增加树的高度,导致性能降低;
- 相对 Hash 索引,B+tree 支持范围匹配及排序操作;