基本概念

State, Action, State transition

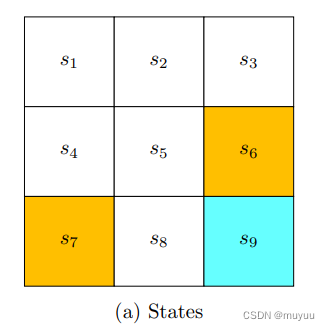
• State: 用于描述agent目前所处的状态，以grid-world为例，即location: $s_1,s_2,...$
  

• Action: 在某个State时，可以做的动作的集合，以grid-world为例，即：
  

• State transition：State转移矩阵（确定情形）or State转移分布（概率情形），以grid-world为例，eg:

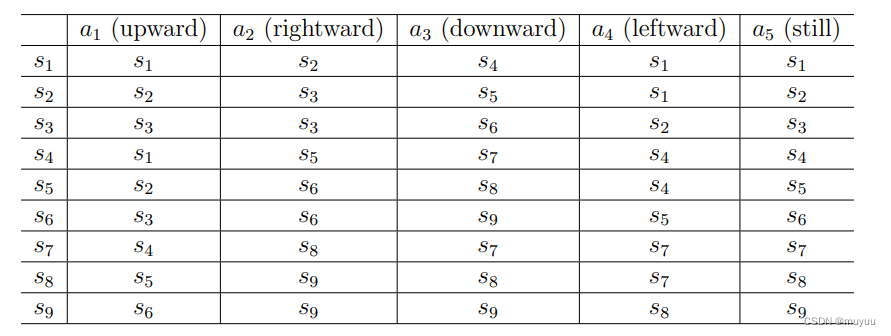
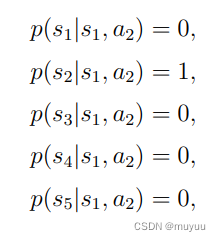
Policy, Reward, Trajectory, Discount Return

• Policy：即策略，告诉agent在每个State时，应该做什么Action，也有（确定形式）和（概率形式）：

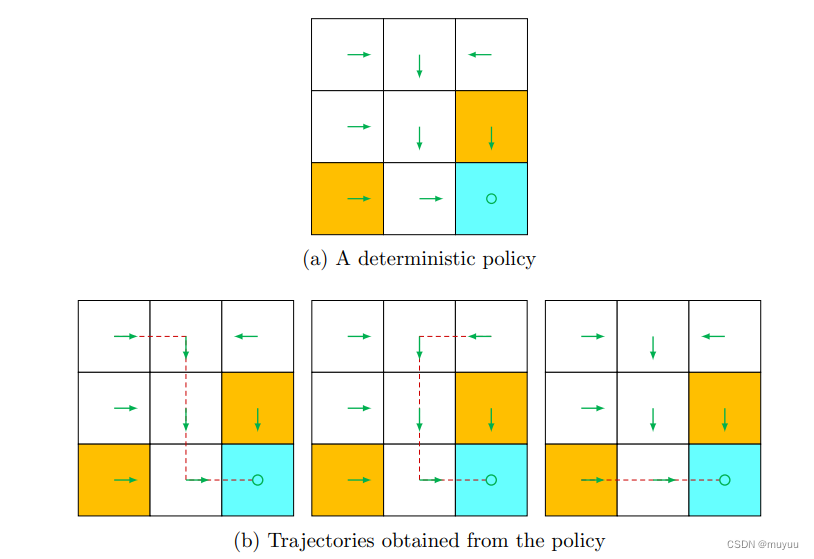
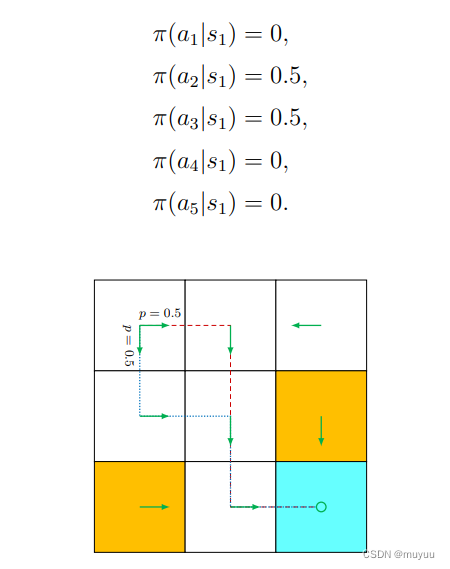
Policy在实际使用时，一般是存为表格（数组）形式，eg:

• Reward：一个实值（标量），eg：正数用于reward，负数用于punishment，数学表达，eg :
  $$\{\begin{array}{l}P(r=1|当前state，当前选择的a_i)=0.8\\ \\ P(r=0|当前state，当前选择的a_i)=0.2\end{array}$$

• Trajectory：即 state-action-reward 链，eg:
  
  

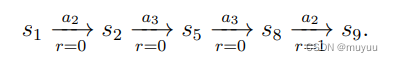
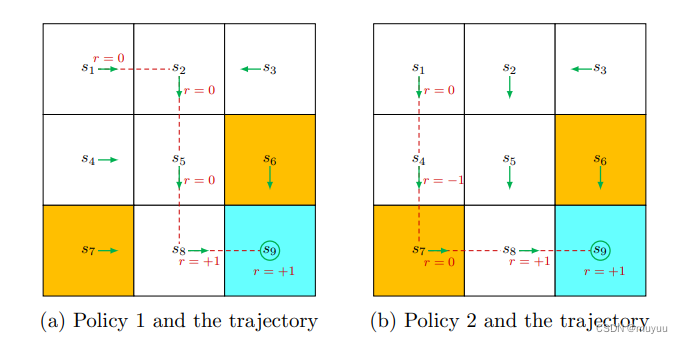
• Return：即一个Trajectory上所有reward之和，eg：上图中第一个return是2，第二个return是1，所以第一个policy更好（没有进到forbidden block）

  由于在到达target $s_9$之后，$s_9$的action会维持在$s_9$，即action一直是$a_5$（维持不动），因此reward会一直+1（那为什么不设置到达target之后停止/退出？），引入 discount rate $\gamma \in (0,1)$：
  $$\begin{array}{rl}\text{discount return}& =0+0\gamma +0{\gamma }^2+1{\gamma }^3+1{\gamma }^4+1{\gamma }^5+...\\ & ={\gamma }^3(1+\gamma +{\gamma }^2+...)={\gamma }^3\frac{1}{1-\gamma }\end{array}$$
  作用是：当$\gamma$更趋于0时，return更受早期的action影响，而当$\gamma$更趋于1时，return更受后期的action的影响

Episode

• Episode：当有terminal state时，即到这个state就停止，称为 episodic task（有限步）；反之称为 continuing task（无限步，现实不存在，但当步数非常多时，近似认为是continuing task）。可以通过以下两种方法将 episodic task 看作特殊的 continuing task，这样后面就只需要对continuing task做理解：
  1. 将terminal state看作特殊的absorbing state（即进到这个stage再也不会离开），且需要将这个state的action的reward都设为0
  2. 将terminal state看作普通的state，可以离开，且每次进入该state时 $r=+1$ (后面采用该种，因为更一般化)

Markov decision process

需要以上几个分布：

1. $\pi (a|s)$，在当前状态s，所做的action的分布 （即Policy）
2. $P(s^{\prime }|s,a)$，在当前状态s，选定了动作a之后，下一个可能到的状态的分布（eg：往下时，即可能往下一格，也可能往下两格）
3. $P(r|s,a)$，在当前状态s，选定了动作a之后，可能的reward （ 跟$P(s^{\prime }|s,a)$属同一分布，即 $s^{\prime }$ 定了reward 就定了；还是说即使 $s^{\prime }$ 定了，reward也仍然不是确定值？）
4. 以及Markov假设：
   $$\begin{array}{rl}P(s_{t+1}|a_{t+1},s_t,...,a_1,s_0)& =P(s_{t+1}|a_{t+1},s_t)\\ P(r_{t+1}|a_{t+1},s_t,...,a_1,s_0)& =P(r_{t+1}|a_{t+1},s_t)\end{array}$$

---

贝尔曼公式

推导确定形式的贝尔曼公式

定义 $v_i$ 为从 $s_i$ 出发的Trajectory的return, eg:

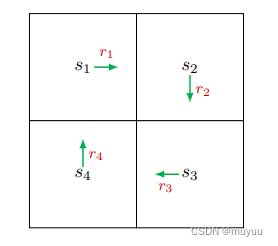
则有 Bootstrapping 推导式：

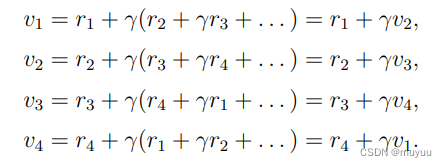
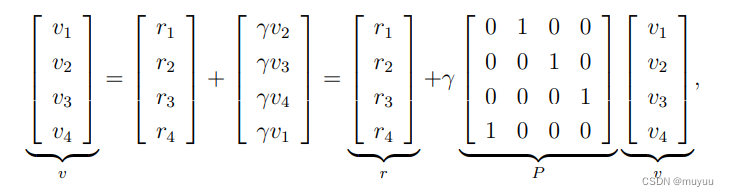
$$\Rightarrow v=r+\gamma Pv$$

$\Rightarrow$ 解析解 : $v=(I-\gamma P{)}^{-1}r$

推导一般形式的贝尔曼公式

State Value

首先给出 State Value 的定义，对于一个multi-step trajectory，其步骤可以表示为：
$$S_t\stackrel{A_t}{\to }{S}_{t+1},R_{t+1}\stackrel{A_{t+1}}{\to }{S}_{t+2},R_{t+2}\stackrel{A_{t+2}}{\to }{S}_{t+3},R_{t+3},...$$

该条从 $S_t$ 出发的 trajectory 的 discounted return 则为：
$$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...$$

由于 $R_{t+1},R_{t+2},...$ 均为随机变量，因此 $G_t$ 也是随机变量。

• State Value：即当前状态为 s 时，discounted return $G_t$ 的期望值：
  $$v_{\pi }(s)=E[G_t|S_t=s]$$

更具象的理解是 :

1. 给定Policy $\pi$ ，当从状态 s 出发时，discounted return的期望值（从一个state出发，可能有多条路径到达terminal/或称多条trajectory，对所有可能的trajectory的discounted return求期望）
2. 某个状态的 $v_{\pi }(s)$ 越高，说明它越有价值/越值得去（见以下例子）

Action Value

State Value 是指从一个 state 出发的 average return，而 Action Value 是指从一个 state 出发，并且 take 某个 action 的 average return。
$$q_{\pi }(s,a)=E[G_t|S_t=s,A_t=a]$$

state value 用于选择哪个 Policy 更好，而 action value 用于选择哪个 action 更好

Action Value 和 State value 的关系：
$$E[G_t|S_t=s]=\sum _{a}E[G_t|S_t=s,A_t=a]\pi (a|s)$$
即：$$v_{\pi }(s)=\sum _a\pi (a|s)q_{\pi }(s,a)$$
$\Rightarrow$ State Value 实际是所有 Action Value 的 “平均”

下面开始推导贝尔曼公式：

由于
$$\begin{array}{rl}{G}_t& =R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...\\ & =R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+...)\\ & =R_{t+1}+\gamma G_{t+1}\end{array}$$

$$\begin{array}{rl}\Rightarrow v_{\pi }(s)& =E[G_t|S_t=s]\\ & =E[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ & =E[R_{t+1}|S_t=s]+\gamma E[G_{t+1}|S_t=s]\end{array}$$

其中第一项为 下一步的reward的期望，可以分解为：
$$\begin{array}{rl}E[R_{t+1}|S_t=s]& =\sum _{a}E[R_{t+1}|S_t=s,A_t=a]\pi (a|s)\\ & =\sum _a\pi (a|s)\sum _{r}P(r|s,a)r\end{array}$$

第二项为 从下一时刻的状态为起点的 trajectory 的 discounted return，可以分解为：
$$\begin{array}{rl}E[G_{t+1}|S_t=s]& =\sum _{s^{\prime }}E[G_{t+1}|S_t=s,S_{t+1}=s^{\prime }]P(s^{\prime }|s)\\ & =\sum _{s^{\prime }}E[G_{t+1}|S_{t+1}=s^{\prime }]P(s^{\prime }|s)\\ & =\sum _{s^{\prime }}{v}_{\pi }(s^{\prime })P(s^{\prime }|s)\\ & =\sum _{s^{\prime }}{v}_{\pi }(s^{\prime })\sum _{a}P(s^{\prime }|s,a)\pi (a|s)\end{array}$$

由上得贝尔曼公式一般形式：
$$\begin{array}{r}{v}_{\pi }(s)=\sum _a\pi (a|s)[\sum _{r}P(r|s,a)r+\gamma \sum _{s^{\prime }}P(s^{\prime }|s,a)v_{\pi }(s^{\prime })],\forall s\end{array}$$
贝尔曼公式描述了 两个 state value $v_{\pi }(s)$ 和 $v_{\pi }(s^{\prime })$ 的关系

同时由 state value 和 action value 的关系：$$v_{\pi }(s)=\sum _a\pi (a|s)q_{\pi }(s,a)$$
可得 $$q_{\pi }(s,a)=\sum _{r}P(r|s,a)r+\gamma \sum _{s^{\prime }}P(s^{\prime }|s,a)v_{\pi }(s^{\prime })$$
即如果知道所有的State Value，反过来也可以求 Action Value

一些例子

1. 对于policy：
   
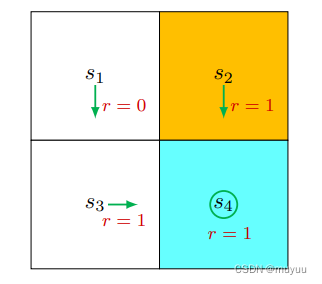
   由于
   $$\begin{array}{rl}& \pi (a=a_3|s_1)=1,\pi (a\ne a_3|s_1)=0\\ & P(s^{\prime }=s_3|s_1,a_3)=1,P(s^{\prime }\ne s_3|s_1,a_3)=0\\ & P(r=0|s_1,a_3)=1,P(r\ne 0|s_1,a_3)=0\end{array}$$

$$\begin{array}{rl}\Rightarrow v_{\pi }(s_1)& =\sum _a\pi (a|s_1)[\sum _{r}P(r|s_1,a)r+\gamma \sum _{s^{\prime }}P(s^{\prime }|s_1,a)v_{\pi }(s^{\prime })]\\ & =1\ast [\sum _{r}P(r|s_1,a_3)r+\gamma \sum _{s^{\prime }}P(s^{\prime }|s_1,a_3)v_{\pi }(s^{\prime })]\\ & =1\ast [1\ast 0+0+\gamma \ast 1\ast v_{\pi }(s_3)]\\ & =0+\gamma v_{\pi }(s_3)\end{array}$$

同理有：
$$\begin{array}{rl}{v}_{\pi }(s_2)& =1+\gamma v_{\pi }(s_4)\\ v_{\pi }(s_3)& =1+\gamma v_{\pi }(s_4)\\ v_{\pi }(s_4)& =1+\gamma v_{\pi }(s_4)\end{array}$$

解得：
$$\begin{array}{rl}{v}_{\pi }(s_1)& =\frac{\gamma }{1-\gamma }\\ v_{\pi }(s_2)& =\frac{1}{1-\gamma }\\ v_{\pi }(s_3)& =\frac{1}{1-\gamma }\\ v_{\pi }(s_4)& =\frac{1}{1-\gamma }\end{array}$$

$$\Rightarrow v_{\pi }(s_1)<v_{\pi }(s_2)=v_{\pi }(s_3)=v_{\pi }(s_4)$$
解释：$s_1$ 距离 target state 比其他 state 都要远，因此其 价值 低于其他的 state，（直观上也可以看到 $s_1$ 距离 target state，比其他的 state 都要远）

---

2. 更复杂的例子
   两种好的 Policy，及其各个 state 的 state value:
   

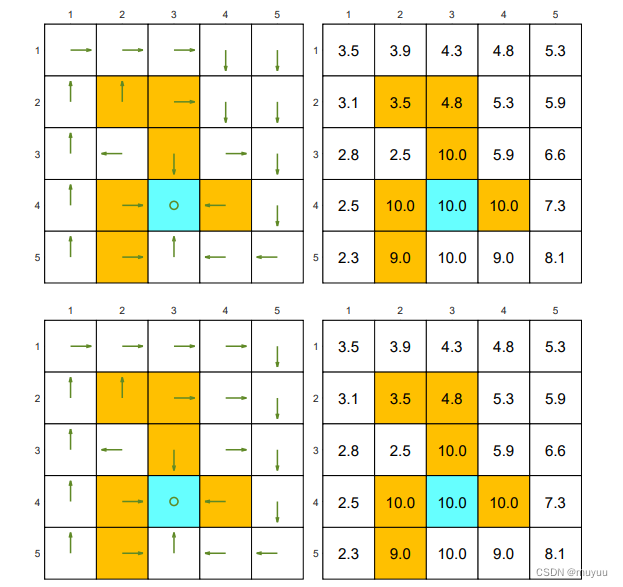
两种不好的 Policy：一个全向右的 Policy 和 一个随机生成的 Policy：

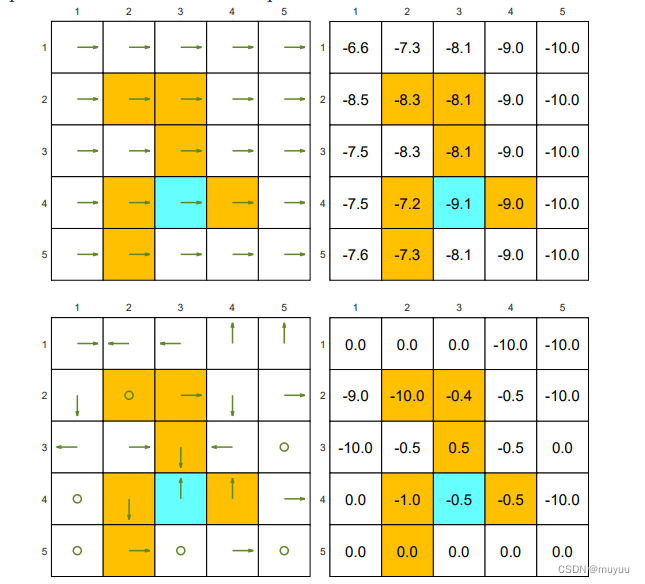
可以看到

1. 好的 Policy 的 state value，基本都为正；而不好的 Policy 的 state value 中，会有很多负数
2. 两个不完全相同的 Policy，也可能有完全一样的 state value （因为在其出现 diff 的部分路径上，reward总和相同）

---

贝尔曼公式的 Matric-vector form

记
$$\begin{array}{rl}{r}_{\pi }(s_i)& =\sum _a\pi (a|s_i)\sum _{r}P(r|s_i,a)r=E[R_{t+1}|S_t=s_i]\end{array}$$

又有：$$P_{\pi }(s_j|s_i)=\sum _{a}P(s_j|s_i,a)\pi (a|s_i)$$

因此 $$v_{\pi }(s_i)=r_{\pi }(s_i)+\gamma \sum _{s_j}{P}_{\pi }(s_j|s_i)v_{\pi }(s_j)$$
Matric-vector form：$$v_{\pi }=r_{\pi }+\gamma P_{\pi }{v}_{\pi }$$

例如：

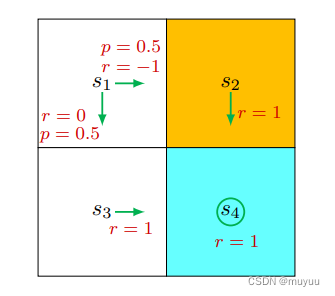
上式可展开为：

贝尔曼公式的解析解和迭代解

贝尔曼公式：$$v_{\pi }=r_{\pi }+\gamma P_{\pi }{v}_{\pi }$$
$$\Rightarrow 解析解：v_{\pi }=(I-\gamma P_{\pi }{)}^{-1}{r}_{\pi }$$
一些理论可得的结论：

1. $(I-\gamma P_{\pi })$ 是可逆的

---

Gershgorin 圆盘定理

设 $A$ 是一个 $n\times n$ 复矩阵，矩阵的元素为 $a_{ij}$。对于每个 $i$，定义 Gershgorin 圆盘 $D_i$ 为以 $a_{ii}$ 为中心，半径为矩阵第 $i$ 行上非对角元素绝对值之和的圆盘。即：

D i = { z ∈ C : ∣ z − a i i ∣ ≤ R i } D_i = \{ z \in \mathbb{C} : |z - a_{ii}| \leq R_i \} Di​={z∈C:∣z−aii​∣≤Ri​}

其中 $R_i={\sum }_{j\ne i}|a_{ij}|$。

Gershgorin 圆盘定理的结论是：矩阵 $A$ 的所有特征值都位于至少一个 Gershgorin 圆盘内。

换句话说，如果我们把矩阵 $A$ 看成是由复数元素构成的，矩阵 $A$ 的特征值在复平面上一定位于这些 Gershgorin 圆盘的并集内。

---

那么根据Gershgorin 圆盘定理，$(I-\gamma P_{\pi })$ 的每个特征值都至少在一个
$$\begin{array}{rl}圆心为& ：[(I-\gamma P_{\pi }){]}_{ii}=1-\gamma P_{\pi }(s_i|s_i)\\ 半径为& ：\sum _{j\ne i}|[I-\gamma P_{\pi }{]}_{ij}|=\sum _{j\ne i}\gamma P_{\pi }(s_j|s_i)（因为j\ne i时，I_{ij}=0）\end{array}$$
的圆当中，又有：

$$\sum _{j\ne i}\gamma P_{\pi }(s_j|s_i)+\gamma P_{\pi }(s_i|s_i)=\gamma <1$$
因此：
$$\sum _{j\ne i}\gamma P_{\pi }(s_j|s_i)<1-\gamma P_{\pi }(s_i|s_i)$$
即 半径 < |圆心|，说明 $(I-\gamma P_{\pi })$ 的 Gershgorin 圆盘都不包含原点，因此其特征值都不为零。

---

2. $(I-\gamma P_{\pi }{)}^{-1}>I$

由泰勒级数展开：$$\frac{1}{1-x}=1+x+x^2+x^3+...$$
$$\Rightarrow (I-\gamma P_{\pi }{)}^{-1}=I+\gamma P_{\pi }+{\gamma }^2{P}_{\pi }^2+...\ge I,(\gamma >0，而P_{\pi }的值是概率，也总大于0)$$

---

不过实际中，$(I-\gamma P_{\pi })$ 是一个很大的矩阵，求逆计算量太大，因此实际一般使用迭代式：
$$v_{k+1}=r_{\pi }+\gamma P_{\pi }{v}_k$$

以上迭代式成立的原因是：
$$v_k\to v_{\pi }=(I-\gamma P_{\pi }{)}^{-1}{r}_{\pi },\text{ as }k\to \infty .$$
证明如下：