【单调栈】1130. 叶值的最小代价生成树

1130. 叶值的最小代价生成树

难度：中等
力扣地址：https://leetcode.cn/problems/minimum-cost-tree-from-leaf-values/description/

题目内容

给你一个正整数数组 arr，考虑所有满足以下条件的二叉树：

每个节点都有 0 个或是 2 个子节点。
数组 arr 中的值与树的中序遍历中每个叶节点的值一一对应。
每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。
在所有这样的二叉树中，返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。

如果一个节点有 0 个子节点，那么该节点为叶节点。

示例 1：
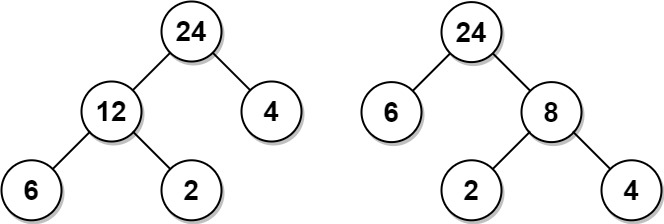
在这里插入图片描述

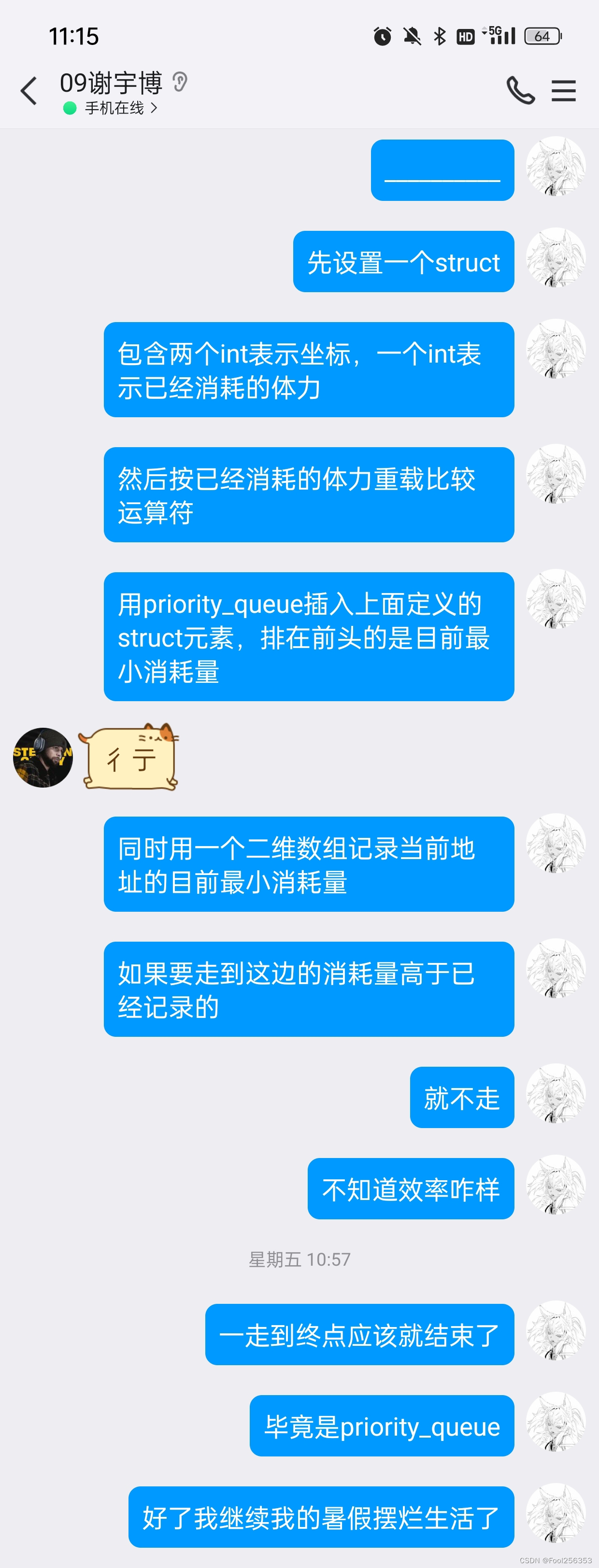
输入：arr = [6,2,4]
输出：32
解释：有两种可能的树，第一种的非叶节点的总和为 36 ，第二种非叶节点的总和为 32 。

示例 2：
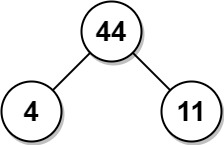
在这里插入图片描述

输入：arr = [4,11]
输出：44

提示：

2 <= arr.length <= 40
1 <= arr[i] <= 15
答案保证是一个 32 位带符号整数，即小于 $2^{31}$ 。

单调栈的应用

题目中有提到过 非叶子结点的值等于它左子树最大值乘以右子树最大值。

所以能否考虑类似于 “降维” 的思路，比如我们已经构建了一个子树，是否能把这个子树当做整科树的一个结点来处理，不需要考虑它的叶子是什么。

比如，原来的树结构转换后不考虑它的叶子结点，结果是一样的，即 30 + 18 + 10
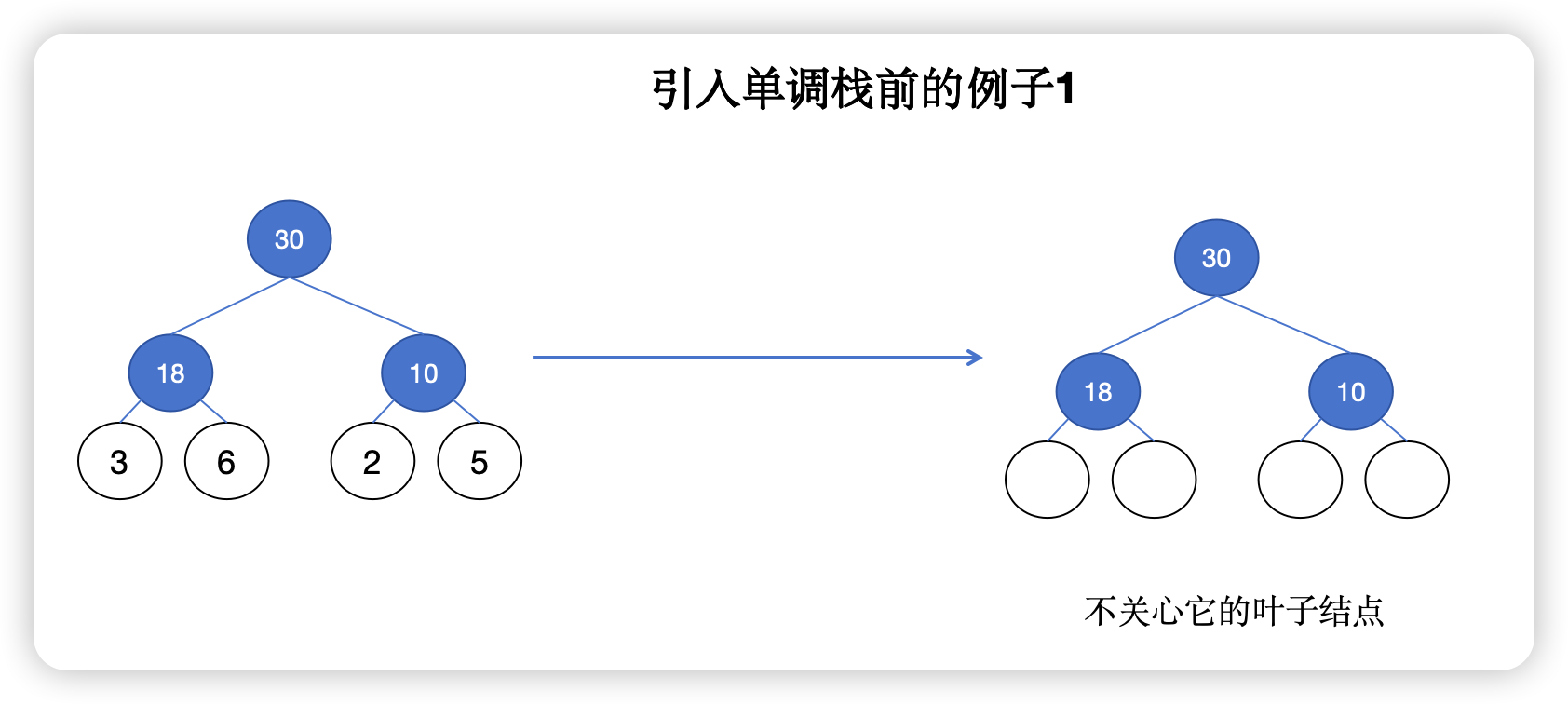
在这里插入图片描述
结论 1：如果已经确定子树，可使用子树的根结点值代替原来的子树（注意转换后不能当作叶子结点）。

得出这个结论的目的，是希望我们能自底向上的构建树结构，并且能够简化构建过程中我们存储的中间结果。

接下来的问题转换为，我们 如何构建子树。

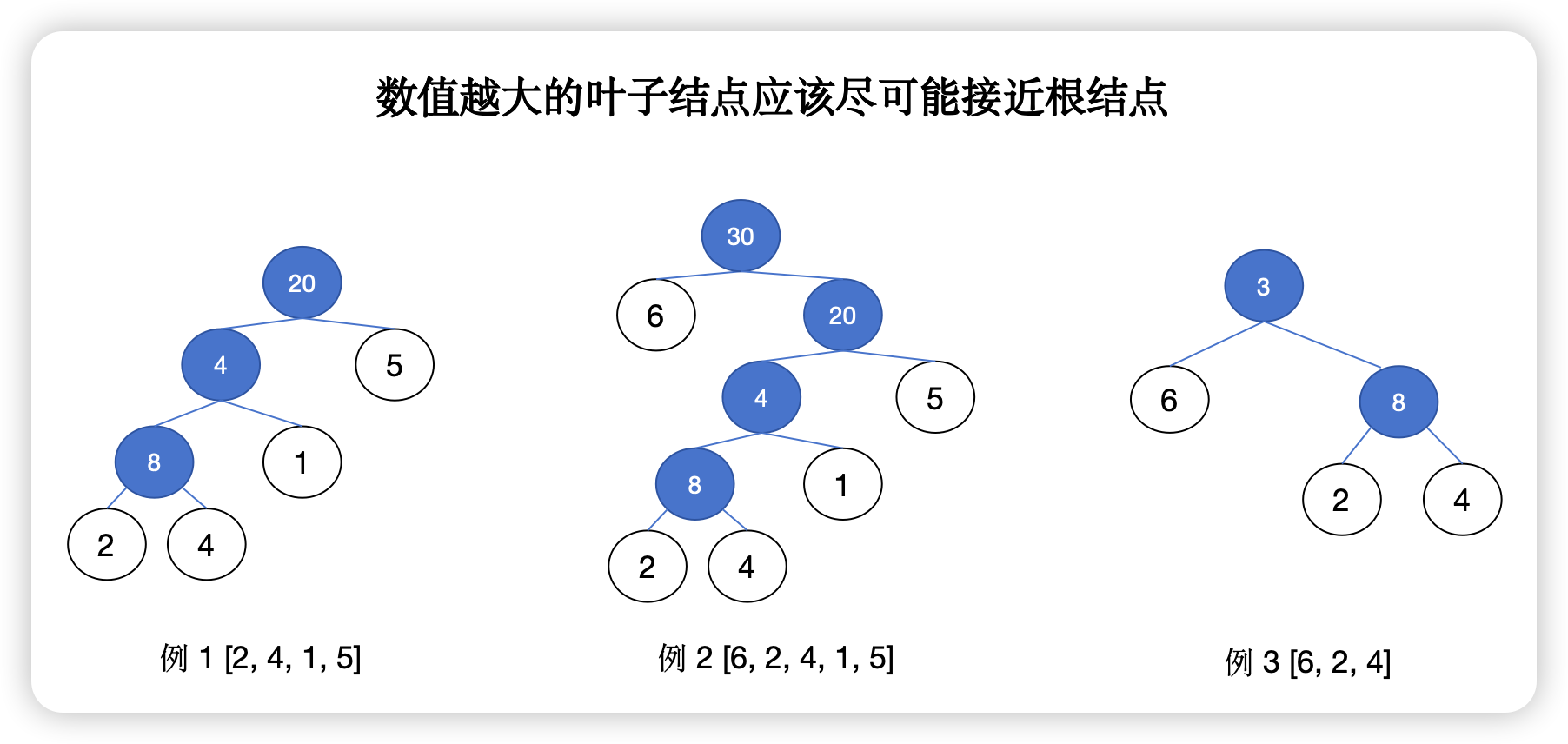
题目的意思是，希望构建叶值的最小代价生成树，并且根据题目的计算逻辑，叶子结点决定它的父结点的值（左右结点最大值的乘积），所以我们应该很容易想到，数值越大的叶子结点应当尽可能靠近根结点 —— 尽可能减少它参与祖辈结点的生成过程。

结论2：数值越大的叶子结点应当尽可能靠近根结点。

下面是几个例子，印证这个观点。

在这里插入图片描述

到目前为止，离解开本题只有 一步之遥 —— 如何利用栈并利用结论 1 与结论 2 来构建目标树，并返回最终结果。

解决方法：利用栈的 “先进后出” 特点，将叶子值最大的压箱底，把比它小的根据条件出栈，并生成可用的子树根结点。

问题 1 什么时候入栈，什么时候出栈
回答：我们需要构建一个严格的单调递减的栈，如果新来的元素破坏了这个规则，则开始出栈，并给新来的元素一个合适的位置；如果新来的元素满足单调递减的规则，则入栈这个元素。比如原有
[3, 2] 新来的元素是 5，明显破坏了单调性规则，需要出栈；比如新来的元素是 1，没有破坏规则，入栈。

问题 2 入栈出栈动作需要做什么
回答：如果只是入栈，则什么都不做；如果是出栈，则需要考虑开始构建子树。

问题3 出栈时，如何构建子树
回答：前面结论1提到，我们不关心子树的具体构成，只是需要生成后的根结点，以及它的左右子树的最大值。因此，出栈构建子树时，需要记录这个子树的所有结点中的最大值。比如 [3, 2] 构建子树，那么它的根结点的值为 6，它子树最大值为 3。

问题 4 如果输入数据是单调递减的，最后怎么出栈
回答：最后从栈顶向下依次出栈，并逐个结点的构建子树。比如 [4, 3, 2, 1] ，首先 2 与 1 构建生成子树 T1，然后让 3 与 T1 结合生成子树 T2，最后 4 与 T2 结合，生成最终树。

问题5 题目中提到的最小代价如何计算
回答：假设我们最终结果为 result，初始化为 0，生成子树的过程，计算得到根结点的值 r1，那么可以明确这个 r1 会参与最后 result 的计算，所以 result += r1，然后记录这个子树的最大值，因为最后根结点的值等于左右子树的最大值的乘积。记录这个子树的最大值的方法，是将这个子树的左右结点最大值入栈，随着出栈的过程派上用场。

基于单调栈计算最小代价生成树例子

例 1 [6, 2, 3, 4]

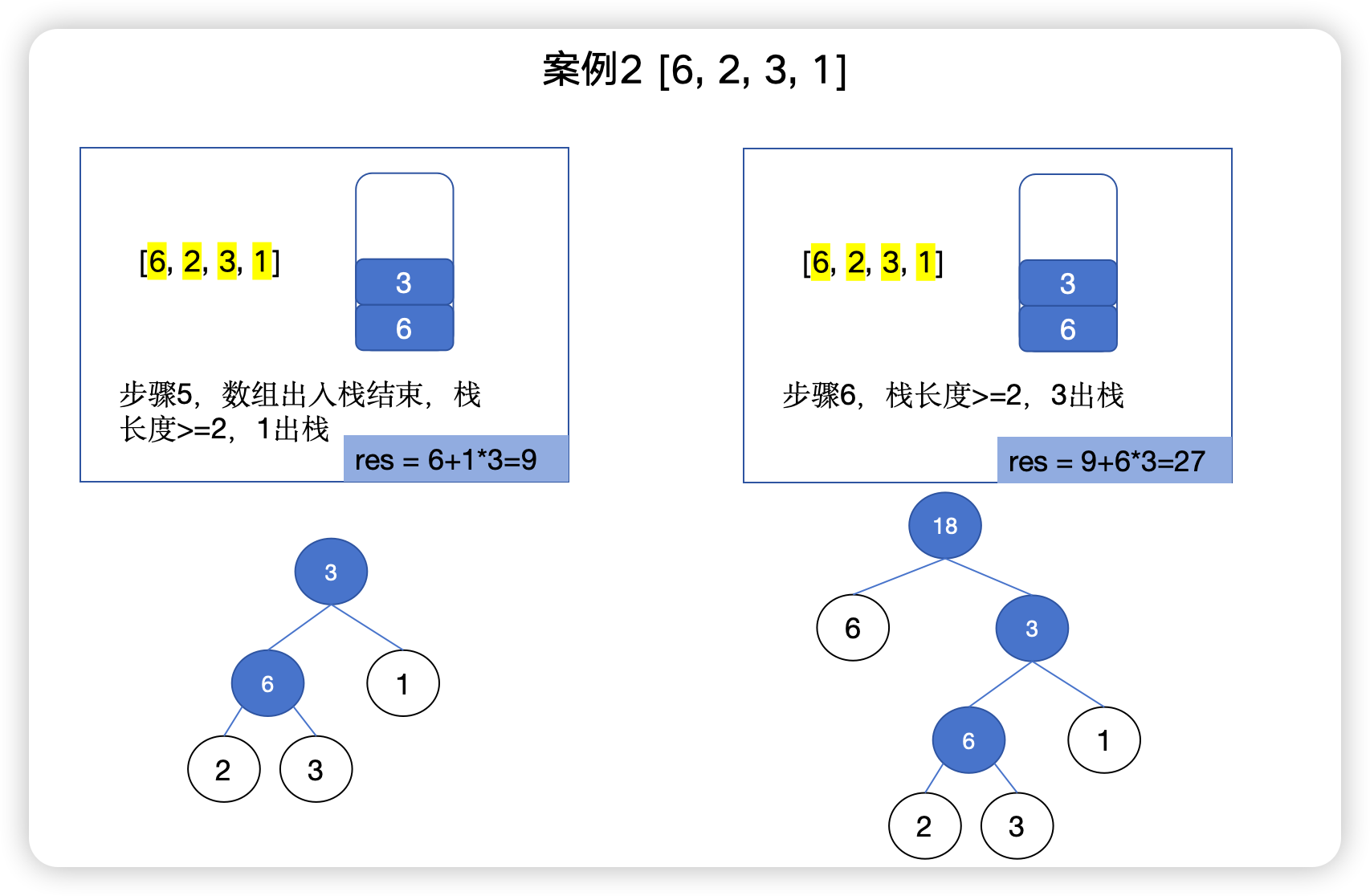
在这里插入图片描述

例 2 [6, 2, 3, 1]

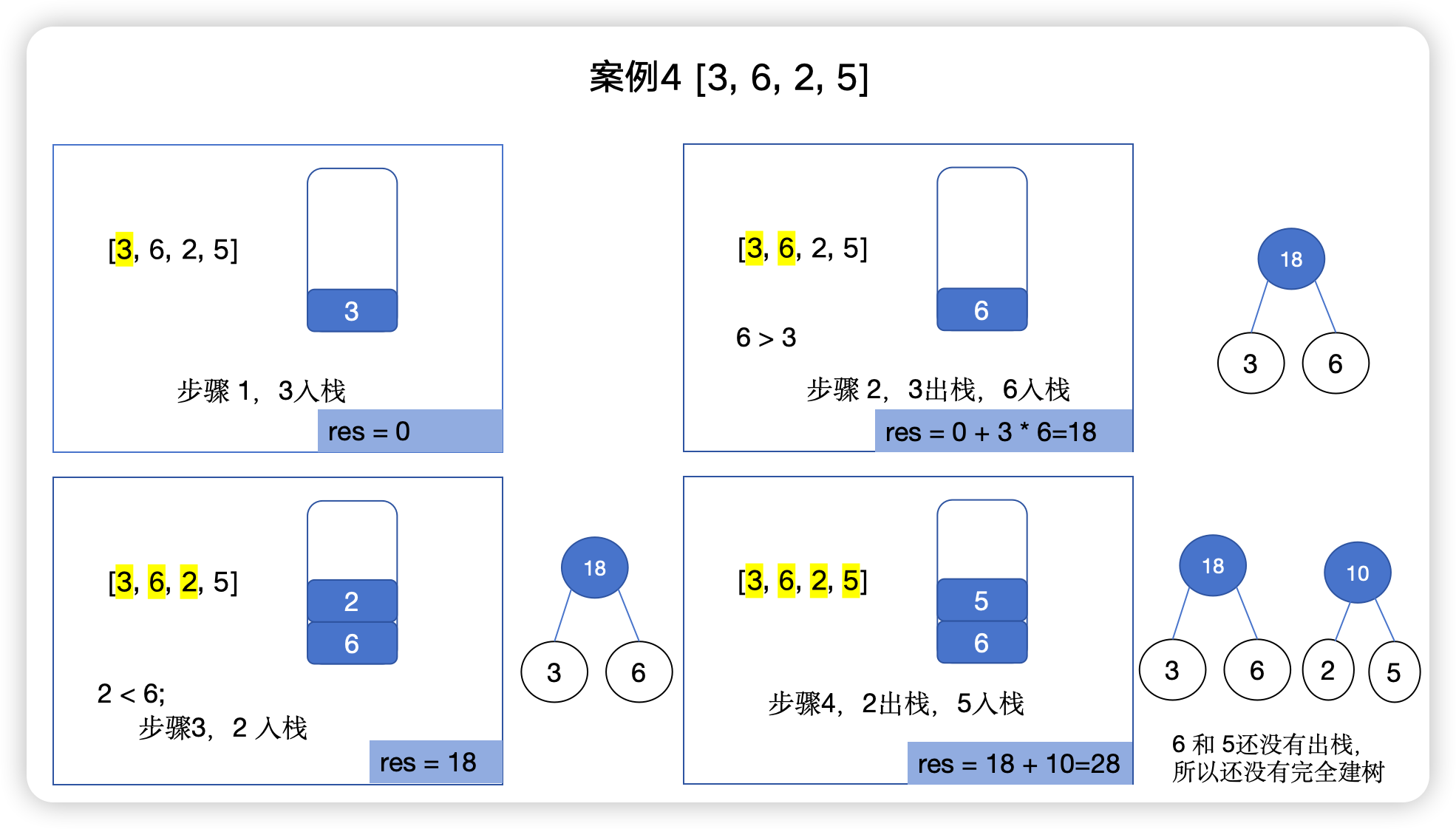
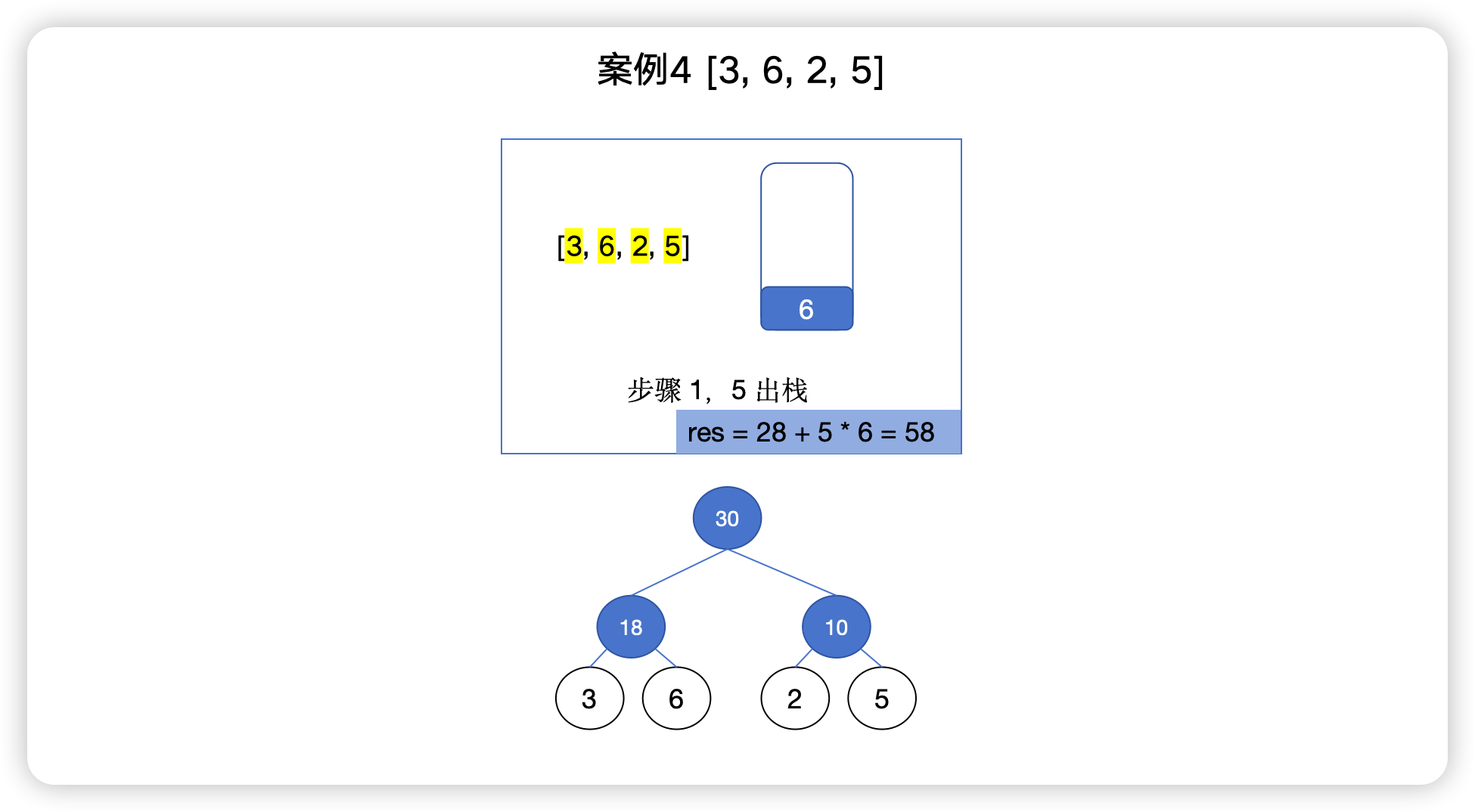
在这里插入图片描述

例 3 [6, 2, 4, 1, 5]

在这里插入图片描述

例 4 [3, 6, 2, 5]

在这里插入图片描述

代码实现

如果使用的是其他语言，也可以参考一下这个 c++ 的实现代码，没有用到 c ++ 什么新特性，理解容易。

class Solution {
public:
    int mctFromLeafValues(vector<int>& arr) {
         // 用于存储节点值的栈，如果子树已经生成，栈内存储的是子树的左右子树各叶子结点的最大值
        stack<int> maxVals;
        // 计算最小代价
        int result = 0;
        for (int value : arr) {
            // 检查是否满足出栈条件
            while (!maxVals.empty() && maxVals.top() <= value) {
                // 要出栈的元素
                int top = maxVals.top();
                // 出栈
                maxVals.pop();
                // 如果栈为空，或者当前值小于栈顶元素（入栈不会破坏单调递减的约定）
                // 则将刚刚出栈的元素，与新来的值 value 生成子树
                // 并计算这个子树的根结点结果
                if (maxVals.empty() || maxVals.top() > value) {
                    result += (top * value);
                } else {
                    // 如果栈不为空，并且栈顶元素小于新来的 value，说明 value 不能简单入栈
                    // 需要挪到期望的位置，所以这个 value 目前不参与子树的构建
                    // 而是将刚刚出栈的，和目前的 top （将要出栈的）结合，生成子树
                    // 可以考虑结合本博客中的例 4 进行理解（步骤4）
                    result += (maxVals.top() * top);
                }
            }
            maxVals.push(value);
        }

        // 还存在未生成树的叶子结点或者子树的根结点（记录的是子树的最大值）
        // 则需要将剩下的出栈，并生成最终的树
        while (maxVals.size() >= 2) {
            int top = maxVals.top();
            maxVals.pop();
            result += top * maxVals.top();
        }
        return result;
    }
};

对应的 python 实现是

class Solution:
    def mctFromLeafValues(self, arr):
        # 用于存储节点值的栈，如果子树已经生成，栈内存储的是子树的左右子树各叶子结点的最大值
        maxVals = []
        # 计算最小代价
        result = 0
        
        for value in arr:
            # 检查是否满足出栈条件
            while maxVals and maxVals[-1] <= value:
                # 要出栈的元素
                top = maxVals.pop()
                # 如果栈为空，或者当前值小于栈顶元素（入栈不会破坏单调递减的约定）
                # 则将刚刚出栈的元素，与新来的值 value 生成子树
                # 并计算这个子树的根结点结果
                if not maxVals or maxVals[-1] > value:
                    result += top * value
                else:
                    # 如果栈不为空，并且栈顶元素小于新来的 value，说明 value 不能简单入栈
                    # 需要挪到期望的位置，所以这个 value 目前不参与子树的构建
                    # 而是将刚刚出栈的，和目前的 top （将要出栈的）结合，生成子树
                    result += maxVals[-1] * top
            
            maxVals.append(value)
        
        # 还存在未生成树的叶子结点或者子树的根结点（记录的是子树的最大值）
        # 则需要将剩下的出栈，并生成最终的树
        while len(maxVals) >= 2:
            top = maxVals.pop()
            result += top * maxVals[-1]
        
        return result

对应的 java 实现为

import java.util.Stack;

class Solution {
    public int mctFromLeafValues(int[] arr) {
        // 用于存储节点值的栈，如果子树已经生成，栈内存储的是子树的左右子树各叶子结点的最大值
        Stack<Integer> maxVals = new Stack<>();
        // 计算最小代价
        int result = 0;
        
        for (int value : arr) {
            // 检查是否满足出栈条件
            while (!maxVals.isEmpty() && maxVals.peek() <= value) {
                // 要出栈的元素
                int top = maxVals.pop();
                // 如果栈为空，或者当前值小于栈顶元素（入栈不会破坏单调递减的约定）
                // 则将刚刚出栈的元素，与新来的值 value 生成子树
                // 并计算这个子树的根结点结果
                if (maxVals.isEmpty() || maxVals.peek() > value) {
                    result += (top * value);
                } else {
                    // 如果栈不为空，并且栈顶元素小于新来的 value，说明 value 不能简单入栈
                    // 需要挪到期望的位置，所以这个 value 目前不参与子树的构建
                    // 而是将刚刚出栈的，和目前的 top （将要出栈的）结合，生成子树
                    result += (maxVals.peek() * top);
                }
            }
            maxVals.push(value);
        }

        // 还存在未生成树的叶子结点或者子树的根结点（记录的是子树的最大值）
        // 则需要将剩下的出栈，并生成最终的树
        while (maxVals.size() >= 2) {
            int top = maxVals.pop();
            result += top * maxVals.peek();
        }
        return result;
    }
}

总结

做题时应当多涂涂画画，研究题目究竟存在什么样的规律。比如 [6, 2, 3, 1] 这种情况，为什么 2 会选择与 3 结合，而不是让 3 与 1 结合。换而言之，我们读数组 [ 6, 2, 3] 时，是否能确定 2 与 3 能生成子树，并且不会因为后面出现的值而影响到。这些问题应当逐个梳理，归纳一些与本题息息相关的结论，然后再去梳理主要流程，编码实现等。