题目（八数码问题）

编号为1-8的8个正方形滑块被摆成3行3列（有一个格子留空），如下图所示

8	1	5
7	3	6
4		2

每次可以把与空格相邻的滑块（有公共边才算相邻）一道空格中，而它原来的位置就成为了新的空格。给定初始局面和目标局面（用0表示空格），你的任务是计算出最少的移动步数。如果无法到达目标局面，则输出-1

解法思路

简单来说就是无权图的最短路径问题（和我昨天看到的魔方问题差不多），可以用bfs来做

如果想看看有权图的最短路径问题，可以看看下面这题：

OpenJudge - 19G:海拔

我做这题的思路：

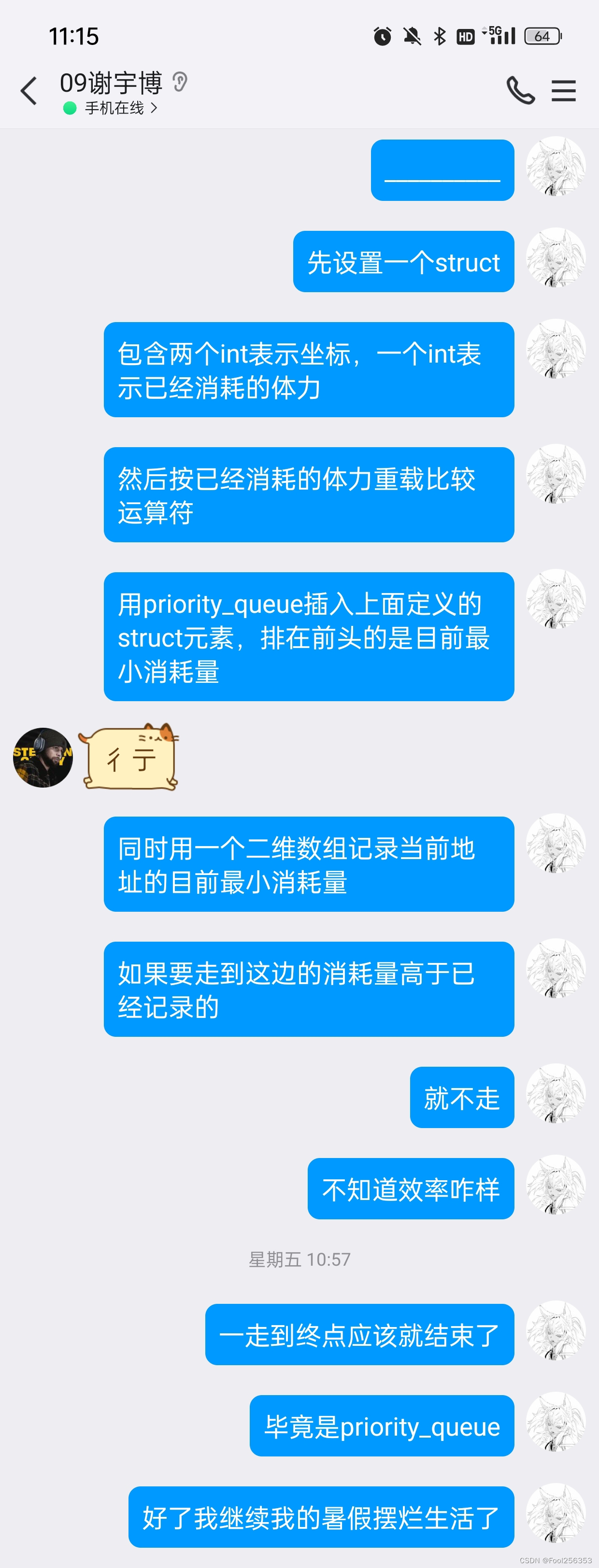
好了言归正传

这题难点在于对状态的记录的问题：如果声明一个9维数组vis，总共有9^9=387420489个项，太多了，内存直呼根本塞不下。如果把9个元素合并成一个数字，最大的数字是876543210，甚至更大

而实际的结点数量并没有这么多，0~8的全排列只有9！= 362990个，如果按照上面的方法，有大量的内存会被浪费

方法一

直接使用STL的集合set。把状态转化为9位十进制整数，就可以用set<int>判重了

set<int> vis;
void init_lookup_table{vis.clear();}
int try_to_insert(int s){
    int v = 0;
    //将s中的状态转化为数字并放入v中（伪代码）
    if(vis.count(v)) return 0;
    vis.insert(v);
    return 1;
}

很简单对吧，但是效率低，建议在时间紧迫或对效率要求不太高的情况下使用

方法二

把排列“变成”整数，然后只开一个一维数组。也就是说，设计一套排列的编码和解码函数，把0~8的全排列和0~362879的整数一一对应起来

int vis[362880], fact[9];
void init_lookup_table(){
    fact[0] = 1;
    for(int i = 1; i < 9; i++) fact[i] = fact[i - 1] * i;
}
int try_to_insert(int s){
    int code = 0; //把st[s]映射到整数code(st为二维数组，记录状态，第二维记录各个数字）
    for(int i = 0; i < 9; i++){
        int cnt = 0;
        for(int j = i + 1; j < 0; j++) if(st[s][j] < st[s][i]) cnt++;
        code += fact[8 - i] * cnt;
    }
    if(vis[code]) return 0;
    return vis[code] = 1;
}

屌吧，屌爆了

原理巧妙（我根本想不到），时间效率也非常高，但编码解码法的适用范围并不大：如果总结点数非常大，编码也会非常大，数组还是开不下

方法三

想必诸位都猜到了

使用哈希技术。简单地说，就是要把结点“变成”整数，但是不必一一对应。换句话说，只需设计一个所谓的哈希函数h(x)，然后将任意结点x映射到某个给定范围[0, M - 1]的整数即可，其中M是程序员根据可用内存大小自选的。在理想情况下，只开一个大小为M的数组就能完成判重，但此时往往会有不同结点的哈希值相同，因此需要把哈希值相同的状态组织成链表

typedef int State[9];
const int hashsize = 1000003;
const int maxstate = 1000000;

State st[maxstate];//状态数组
int head[hashsize], next[maxstate];
void init_lookup_table(){memset(head, 0, sizeof(head);}
int hash(State &s){
    int v = 0;
    for(int i = 0; i < 9; i++) v = v * 10 + s[i];//把9个数字组成9位数
    return v % hashsize;//确保哈希值是不超过哈希表大小的非负整数
}
int try_to_insert(int s){
    int h = hash(st[s]);
    int u = head[h];
    while(u){
        if(memcmp(st[u], st[s], sizeof(st[s])) == 0) return 0;//找到了，不用插入
        u = next[u];//继续找
    }
    next[s] = head[h];
    head[h] = s;
    return 1;
}