区间问题——905. 区间选点

news2024/10/7 4:22:39

区间问题

定义

运用情况

注意事项

解题思路

AcWing 905. 区间选点

题目描述

运行代码

代码思路

改进思路

其它代码

代码思路

区间问题

定义

区间通常是指一个连续的范围，可以用数轴上的一段来表示。

运用情况

在数学中广泛用于表示变量的取值范围，如函数的定义域、值域等。
在统计学中用于描述数据的分布区间。
在实际生活中，如时间区间、温度区间等。

注意事项

明确区间的端点是否包含在内（开区间或闭区间）。
对于多个区间的组合，要仔细分析它们之间的关系。
在计算和推理时，要确保区间的定义和条件始终一致。

解题思路

首先确定区间的类型（开区间、闭区间等）。
根据题目条件，列出相关方程或不等式来确定区间的范围。
对于复杂的区间问题，可以通过图形来辅助理解和分析。
检查答案是否满足区间的定义和题目要求。

AcWing 905. 区间选点

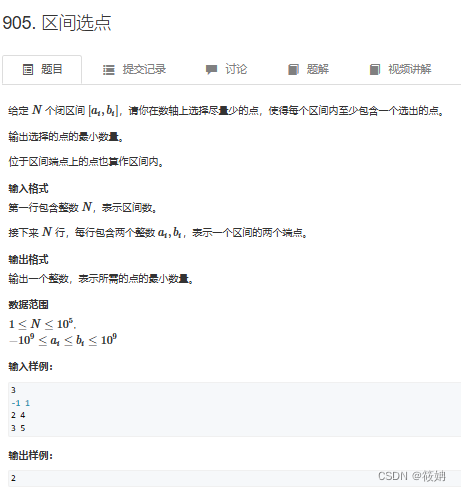
题目描述

905. 区间选点 - AcWing题库

运行代码

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
    int n;
    cin >> n;
    vector<pair<int, int>> intervals(n);
    for (int i = 0; i < n; i++) {
        cin >> intervals[i].first >> intervals[i].second;
    }
    sort(intervals.begin(), intervals.end(), [](const pair<int, int>& a, const pair<int, int>& b) {
        return a.second < b.second;
    });
    int ans = 0, lastPoint = -1000000001;
    for (const auto& interval : intervals) {
        if (interval.first > lastPoint) {
            ans++;
            lastPoint = interval.second;
        }
    }
    cout << ans << endl;
return 0;
}

代码思路

首先，读取区间的数量 n。
创建一个 vector<pair<int, int>> 来存储所有的区间。
通过循环读取每个区间的左右端点并存储到 intervals 中。
然后对区间按照右端点进行排序，这样可以保证先处理右边界较小的区间。
初始化结果 ans 为 0，以及一个表示上一个选择的点的位置 lastPoint 为一个极小值。
遍历排序后的区间：如果当前区间的左端点大于上一个选择的点的位置，说明需要在这个区间内选择一个新的点，将结果加 1，并更新 lastPoint 为当前区间的右端点。这样就可以保证每个区间都至少有一个点被选中，且是尽可能少的点。最后输出结果。
这种贪心策略的核心在于优先处理右边界较小的区间，通过不断更新选择点的位置来满足所有区间的覆盖要求。

改进思路

添加输入有效性检查：可以在读取 n 以及区间端点值时，添加一些检查来确保输入数据的合法性。
考虑使用更高效的数据结构：如果对性能要求较高，可以研究是否有更适合的数据结构来存储和处理区间信息。
添加必要的注释：进一步增加代码的注释，以提高代码的可理解性。
异常处理：考虑添加一些针对可能出现的异常情况（如输入错误、排序失败等）的处理机制。
代码重构：对一些逻辑部分进行重构，使其结构更加清晰，逻辑更加简洁。
性能优化：分析代码中可能存在的性能瓶颈，进行针对性优化，比如尝试不同的排序算法等。

其它代码

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
struct R
{
    int l, r;
    bool operator < (const R &W)const
    {
        return r < W.r;
    }
}r[N];
int main()
{
    int n; cin >> n;
    for(int i = 0; i < n ; i++)
    {
        int a, b; cin >> a >> b;
        r[i] = {a, b};
    }
    sort(r, r + n);
    int ans = 0, right = -2e9;
    for(int i = 0; i < n; i++)
    {
        if(r[i].l > right)
        {
            ans ++;
            right = r[i].r;
        }
    }
    cout << ans << endl;
    return 0;
}

代码思路

定义了一个结构体 R 来表示区间，包含左端点 l 和右端点 r，并定义了结构体之间的比较运算符，按照右端点从小到大排序。
在 main 函数中，首先输入区间的数量 n，然后依次输入每个区间的左右端点，并将其存储在 r 数组中。
通过 sort 函数对区间数组按照右端点排序。
然后通过遍历数组，使用一个变量 right 来记录当前已经覆盖到的最右端位置。如果当前区间的左端点大于 right，说明这是一个新的不重叠区间，就将结果加 1，并更新 right 为当前区间的右端点。最后输出不重叠区间的数量。