1.c++虚函数

        虚函数是用来实现多态(polymorphism) 的一种机制。通过使用虚函数，可以在子类中重写父类中定义的方法，并且在运行时动态地确定要调用哪个方法。

        在类定义中将一个成员函数声明为虚函数，需要使用 virtual 关键字进行修饰 。

        通过指向派生类对象的基类指针或引用调用虚函数时，程序会根据对象的实际类型来调用相应的方法。

2.Softmax函数和Sigmoid函数的区别与联系

Sigmoid函数

        Sigmoid =多标签分类问题=多个正确答案=非独占输出（例如胸部X光检查、住院）。构建分类器，解决有多个正确答案的问题时，用Sigmoid函数分别处理各个原始输出。

        Sigmoid函数是一种logistic函数，它将任意的值转换到  之间

        

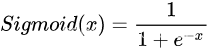
Softmax =多类别分类问题=只有一个正确答案=互斥输出（例如手写数字，鸢尾花）。构建分类器，解决只有唯一正确答案的问题时，用Softmax函数处理各个原始输出值。Softmax函数的分母综合了原始输出值的所有因素，这意味着，Softmax函数得到的不同概率之间相互关联。

        

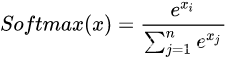
        Softmax函数是二分类函数Sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来。

        Softmax可以由三个不同的角度来解释。从不同角度来看softmax函数，可以对其应用场景有更深刻的理解：

        （1）softmax可以当作arg max的一种平滑近似，与arg max操作中暴力地选出一个最大值（产生一个one-hot向量）不同，softmax将这种输出作了一定的平滑，即将one-hot输出中最大值对应的1按输入元素值的大小分配给其他位置。

        （2）softmax将输入向量归一化映射到一个类别概率分布，即  

个类别上的概率分布（前文也有提到）。这也是为什么在深度学习中常常将softmax作为MLP的最后一层，并配合以交叉熵损失函数（对分布间差异的一种度量）。

        （3）从概率图模型的角度来看，softmax的这种形式可以理解为一个概率无向图上的联合概率。因此你会发现，条件最大熵模型与softmax回归模型实际上是一致的，诸如这样的例子还有很多。由于概率图模型很大程度上借用了一些热力学系统的理论，因此也可以从物理系统的角度赋予softmax一定的内涵。

总结

        如果模型输出为非互斥类别，且可以同时选择多个类别，则采用Sigmoid函数计算该网络的原始输出值。如果模型输出为互斥类别，且只能选择一个类别，则采用Softmax函数计算该网络的原始输出值。Sigmoid函数可以用来解决多标签问题，Softmax函数用来解决单标签问题。[1]对于某个分类场景，当Softmax函数能用时，Sigmoid函数一定可以用。

二分类任务

        对于二分类问题来说，理论上，两者是没有任何区别的。由于我们现在用的Pytorch、TensorFlow等框架计算矩阵方式的问题，导致两者在反向传播的过程中还是有区别的。实验结果表明，两者还是存在差异的，对于不同的分类模型，可能Sigmoid函数效果好，也可能是Softmax函数效果。

3.l1和l2正则化的区别是什么

        L1/L2的区别

        L1是模型各个参数的绝对值之和。L2是模型各个参数的平方和的开方值。

        L1会趋向于产生少量的特征，而其他的特征都是0。

        因为最优的参数值很大概率出现在坐标轴上，这样就会导致某一维的权重为0 ，产生稀疏权重矩阵

     L2会选择更多的特征，这些特征都会接近于0。  

     最优的参数值很小概率出现在坐标轴上，因此每一维的参数都不会是0。当最小化||w||时，就会使每一项趋近于0。

        L1的作用是为了矩阵稀疏化。假设的是模型的参数取值满足拉普拉斯分布。

        L2的作用是为了使模型更平滑，得到更好的泛化能力。假设的是参数是满足高斯分布。

4.介绍svm算法

        是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机。

        SVM可分为三种：

        线性可分SVM

        当训练数据线性可分时，通过最大化硬间隔（hard margin）可以学习得到一个线性分类器，即硬间隔SVM。

        线性SVM

        当训练数据不能线性可分但是近似线性可分时，通过最大化软间隔（soft margin）也可以学习到一个线性分类器，即软间隔SVM。

        非线性SVM

        当训练数据线性不可分时，通过使用核技巧（kernel trick）和最大化软间隔，可以学习到一个非线性SVM。

        SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

        SVM如何选择核函数

        Linear核：主要用于线性可分的情形。参数少，速度快，对于一般数据，分类效果已经很理想了。

        RBF核：主要用于线性不可分的情形。参数多，分类结果非常依赖于参数。有很多人是通过训练数据的交叉验证来寻找合适的参数，不过这个过程比较耗时。

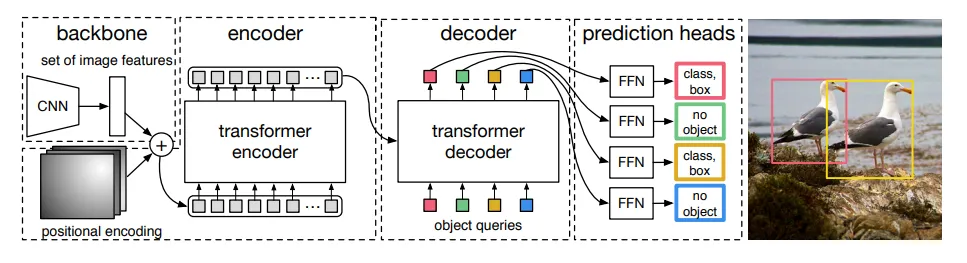
5.介绍transformer算法

        Transformer本身是一个典型的encoder-decoder模型，Encoder端和Decoder端均有6个Block，Encoder端的Block包括两个模块，多头self-attention模块以及一个前馈神经网络模块；Decoder端的Block包括三个模块，多头self-attention模块，多头Encoder-Decoder attention交互模块，以及一个前馈神经网络模块；需要注意：Encoder端和Decoder端中的每个模块都有残差层和Layer Normalization层。

6.1x1大小的卷积核的作用

        通过控制卷积核个数实现升维或者降维，从而减少模型参数。

        对不同特征进行归一化操作。

        用于不同channel上特征的融合。

7.空洞卷积及其优缺点

        pooling操作虽然能增大感受野，但是会丢失一些信息。空洞卷积在卷积核中插入权重为0的值，因此每次卷积中会skip掉一些像素点；

        空洞卷积增大了卷积输出每个点的感受野，并且不像pooling会丢失信息，在图像需要全局信息或者需要较长sequence依赖的语音序列问题上有着较广泛的应用。

8.介绍Transformer中的Q K V

• q代表的是query查询，后续会和每一个k进行匹配，找到最相似的k
• k代表的是key关键字，后续会被每一个q匹配
• v代表的是value值，代表从输入中提到的信息
• Q、K、V概念来源于检索系统，其中Q为Query、K为Key、V为Value。可以简单理解为Q与K进行相似度匹配，匹配后取得的结果就是V。举个例子我们在某宝上搜索东西，输入的搜索关键词就是Q，商品对应的描述就是K，Q与K匹配成功后搜索出来的商品就是V。

        注意：每一个key，都对应一个value；计算query和key的匹配程度就是计算两者相关性，相关性越大，代表key对应value的权重也就越大，这就是不同信息的权重不一样，这就是注意力机制！

例如：

        图书馆里有很多书（value），为了方便查找，我们给书做了编号（key）。当我们想要了解漫威这本书（query）的时候，我们就可以看看那些动漫、电影、甚至二战（美国队长）相关的书籍。

9.self-attention的公式

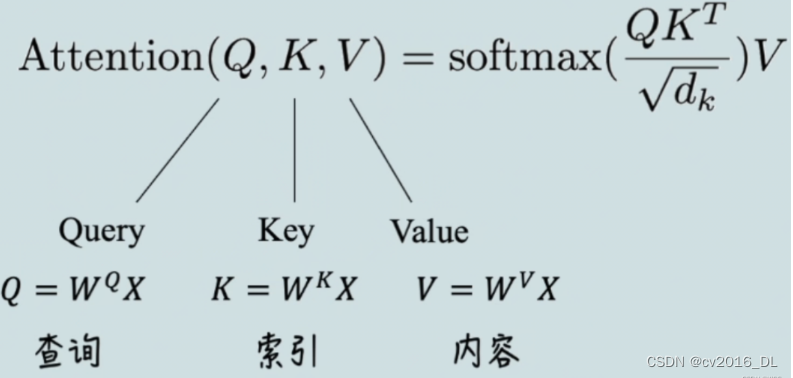
         其中，X XX表示输入的数据，Q , K , V Q,K,VQ,K,V对应内容如图，其值都是通过X XX和超参（先初始化，后通过训练优化）进行矩阵运算得来的。

        可以理解为：Self-Attention中的Q是对自身（self）输入的变换，而在传统的Attention中，Q来自于外部。

10.目标跟踪算法中卡尔曼滤波的作用是什么

         其有两个前提假设：

        系统对运动的建模是线性（linear）的；

        噪声是符合正态分布（Gaussian）的；

1.卡尔曼滤波（Kalman filtering）是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波)过程。​

2、在跟踪中卡尔曼滤波可以基于目标前一时刻的位置，来预测当前时刻的位置，并且可以比传感器更准确的估计目标的位置。

3.卡尔曼滤波不需要前面的历史数据，只需要前一时刻的状态数据就可以进行预测。

11.Focal loss介绍

        FOCAL LOSS是一种针对样本不平衡问题的一种损失函数，用于解决分类器在处理高度偏斜数据集时的困难问题。具体来说，FOCAL LOSS通过调整常规交叉熵损失函数中每个正负样本的权重，使得模型更加关注那些难以分类的样本，从而提高模型在少数类上的分类准确率。

        FOCAL LOSS最初由Lin等人于2017年在论文"Focal Loss for Dense Object Detection"中提出，主要应用于目标检测任务中的多目标分类问题。该损失函数的表达式如下：

        $$FL(p_t)=-(1-p_t)^\gamma\log(p_t)$$

        其中，$p_t$是模型预测的概率值，$\gamma$是一个可调整的超参数，用于控制难易样本的权重。当$\gamma$=0时，FOCAL LOSS退化为普通的交叉熵损失；当$\gamma>0$时，FOCAL LOSS会降低容易分类的样本的权重，增加难分类样本的权重。

        FOCAL LOSS的主要思想是通过降低简单样本的权重，增加难分类样本的权重，来达到处理不平衡数据的目的。在实践中，FOCAL LOSS已经被广泛地应用于各种图像分类、目标检测和语义分割等任务中，取得了较好的效果。

12.匈牙利分配

参考：采用匈牙利算法求解分配问题_匈牙利分配算法-CSDN博客

        分配问题也称指派问题，是一种特殊的整数规划问题，分配问题的要求一般是这样的：n个人分配n项任务

        简单的说：就是n*n矩阵中，选取n个元素，每行每列各有一个元素，使得和最小。

 什么是匈牙利算法？

 1）理论基础：

        若从指派问题的系数矩阵的某行（列）各元素中分别减去或者加上常数k，其最优任务分配问题不变。

         2）匈牙利算法的流程图

        Step 1: 行归约

        找出每行的最小元素，分别从每行中减去这个最小元素；

        Step 2 : 列归约

        找出每列的最小元素，分别从每列中减去这个最小元素

        经过以上两步变换，矩阵的每行每列都至少有了一个零元素。接下来就进行第三步，试着指派任务。

        Step 3 : 指派任务

① 确定独立零元素。

i 从第一行(列)开始，若该行（列）中只有一个零元素，对该零元素标1，表示这个任务就指派给某人做。

每标一个1，同时将该零元素同列的其他零元素标为2，表示此任务已不能由其他人来做。（此处标1、2的操作与课本画圈、划去操作同理）

如此反复进行，直到系数矩阵中所有的零元素都已经被标为1或者2为止。

② 指派

我们观察到，系数矩阵中标记为1的零元素正好等于4，这表示已经确定了最优的指派方案。

此时，只需将0（1）所在位置记为1，其余位置记为0，则获得了该问题的最优解。

异常情况

上例仅为一种理想情况正常情况下，我们在对支付矩阵进行变换时会出现两种情况：

① 出现零元素的闭合回路

②标记成1的元素个数小于n

这两种情况导致支付矩阵中独立零元素出现不足。

i.出现零元素的闭合回路（有多于两行或两列存在两个以上的零元素。）

图的第一行的一二列零元素和第四行的一二列零元素构成回路

这里我们的处理方法是：

先对cost方阵做一个备份（因为会出现多解），然后我们可以顺着回路的走向，对间隔的零元素标记成1，然后对标记成1的零元素所有的行列划一条直线，把这两条直线的其他零元素标记成2,得到一种结果后，再求出多解。

ii. 矩阵中所有标记成1的零元素小于n

因此，我们需要对其进行【画盖0线】的操作。（即画出可以覆盖最多0元素的直线）

（1）画盖0线：利用最少的水平线和垂直线覆盖所有的零。

具体操作如下：

① 对没有标记为1的零元素所在的行打√；

②在已打“√”的行中，对标记为2的零元素所在列打√

③ 在已打“√”的列中，对标记为1的零元素所在行打“√”

④重复②和③，直到再不能找到可以打√的行或列为止。

⑤对没有打“√”的行画一横线，对打“√”的列画一垂线，这样就得到了覆盖所有零元素的最少直线数目的直线集合。

（2）继续变换系数矩阵

①在未被覆盖的元素中找出一个最小元素。

②对未被覆盖的元素所在行中各元素都减去这一最小元素。这时已被覆盖的元素中会出现负元素。

③对负元素所在的列中各元素加上这一最小元素。

Step4

我们发现，在经过一次变换后，独立零元素的个数仍然少于4.此时返回第三步，反复进行，直到矩阵中每一行都有一个被标记为1的元素为止。

13.Mosaic数据增强方法

        Mosaic是一种数据增强方法，可以用于训练物体检测模型，其中在随机裁剪的4张图片上进行拼接，以生成一个大的马赛克图像。

        在YOLOv4中，Mosaic数据增强可以通过以下步骤实现：

1. 随机选择四张不同的图片。
2. 对这四张图片进行随机的缩放和平移操作，使它们的大小、位置不同。
3. 将这四张图片按照某种规则进行拼接，形成一个大的马赛克图像。通常情况下，将四张图片分别放置在左上、右上、左下和右下的位置上，然后进行拼接。
4. 在拼接后的大图像上进行随机裁剪，得到多个大小不同的子图像。
5. 对每个子图像进行标注，并将它们作为训练数据输入给YOLOv4模型进行训练。

通过使用Mosaic数据增强，可以有效地增加训练数据的多样性，提高模型的准确率和鲁棒性。此外，由于Mosaic数据增强可以同时使用多张图片进行训练，因此可以节省GPU内存，提高训练效率。

14.协方差

        协方差是用来衡量两个变量之间线性相关程度的统计量，它描述的是这两个变量同时偏离自身均值时所产生的期望值。协方差可以是正数、负数或者零。

        具体来说，如果两个变量的协方差为正数，则表明这两个变量的变化趋势是相同的；如果协方差为负数，则表明这两个变量的变化趋势是相反的；如果协方差为零，则表明这两个变量之间不存在线性相关关系。

        协方差可以用以下公式来计算：

        cov(X,Y) = E[(X-μ_X)(Y-μ_Y)]

        其中，X和Y是要计算协方差的两个随机变量，μ_X和μ_Y分别是这两个随机变量的均值，E[ ]表示期望值运算符。

        在实际应用中，协方差通常被用作衡量两个变量之间的联合变化程度。例如，当我们研究两种产品的销售量时，可以计算它们的销售量之间的协方差，以了解它们之间的关系强度。另外，在金融领域，协方差也常被用于构建投资组合模型，以评估不同投资品种之间的风险和收益关系。

15.BN的理论

Batch Norm的优点：

• 可以使用大的学习率加快训练
• 使得网络对权重初始化依赖程度降低
• 可以缓解网络的过拟合问题

训练时，以mini-batch为单位，进行归一化操作。如下计算公式：

        对mini-batch中m个数据计算均值和方差，之后通过减去均值，除以标准差的变换，将输入数据分布重新调整到均值为0、方差为1。

    接下来，BatchNorm层会对归一化后的数据利用下述公式进行缩放和平移的变换：

    初始化时，γ = 1， β = 0，之后再通过训练迭代，将这两个超参数调整到合适的值。

    加入平移和缩放的原因是，不一定所有数据都服从标准正态分布，通过平移和缩放可以使得归一化后的数据保留原有学习来的特征，同时还完成归一化操作，加速了训练。

因此BN层是以mini-batch为单位，沿着通道维度进行的：

算法如下：

需要注意的是，

• 在训练时，需要利用每一批数据(batch)计算均值和方差。
• 在测试时，用训练中通过移动平均法保存的均值和方差作为参数。
• 当一个模型训练完成之后，BN层所有参数：均值、方差、γ和β就都确定了。

    BN层的反向传播过程利用链式求导法则，求解dγ、dβ和dx即可。需要强调的是求解dx。均值、方差也都是包含x的函数，因此对x求导时，需要考虑进去，推导过程比较繁琐，可以用batch=2只有x1,x2两个输入情况进行推导，之后推广到batch=m

注意到代码中：

1. beta、gamma在训练状态下，是可训练参数，在推理状态下，直接加载训练好的数值。

2. moving_mean、moving_var在训练、推理中都是不可训练参数，只根据滑动平均计算公式更新数值，不会随着网络的训练BP而改变数值；在推理时，直接加载储存计算好的滑动平均之后的数值，作为推理时的均值和方差。