数据分析：置换检验Permutation Test

news2024/11/18 23:45:01

欢迎大家关注全网生信学习者系列：

WX公zhong号：生信学习者
Xiao hong书：生信学习者
知hu：生信学习者
CDSN：生信学习者2

介绍

置换检验是一种非参数统计方法，它不依赖于数据的分布形态，因此特别适用于小样本数据集，尤其是当样本总体分布未知或不符合传统参数检验的假设条件时。置换检验的基本思想是通过随机置换样本来评估观察到的统计量是否显著不同于随机情况下的预期值。最初真正认识置换检验是从PERMANOVA分析开始的，PERMANOVA的原理是：

原始统计量的获取： 首先计算组间距离的平方和与组内距离的平方和之间的差值。这个差值在统计学中类似于F分布统计量，用于评估组间差异的显著性。
随机置换样本： 接下来，通过随机抽取样本并重新分组，重复计算上述类似F分布的统计量。这个过程需要进行多次，例如1000次，以模拟在随机条件下可能得到的各种统计量值。
统计量分布的构建与评估： 将第二步中重复计算得到的1000个统计量值组成一个分布。然后，观察原始统计量值在这个分布中的位置。如果在显著性水平（例如0.05）的两端，即表示原始统计量值在随机情况下出现的概率较低，从而可以认为存在显著差异；如果不是，则不能拒绝原假设，即认为没有显著差异。

置换检验的应用：

置换检验方法通常用于小样本组间的比较，它不对样本的总体分布提出要求。这种方法特别适用于那些样本量较小，以至于无法使用传统的参数检验（如t检验）的情况。然而，如果使用基于简单假设检验的统计量，例如在评估两组数据差异时，首先通过t检验获得原始t统计量，然后通过置换检验重新抽取样本并计算t统计量，最后评估原始t统计量在由置换得到的t统计量分布中的位置，此时就需要考虑数据的分布特性。这种方法允许研究者在不依赖于数据分布的前提下，对统计显著性进行更为稳健的评估。

加载R包

library(tidyverse)
library(multcomp)
library(lmPerm)

# rm(list = ls())
options(stringsAsFactors = F)
options(future.globals.maxSize = 1000 * 1024^2)

小样本数据案例

现有两组数据，一组是对照组，一组是实验组，它们的样本量分别是3和5，通过以下数据是否能够证实实验处理可以改善结果？

对照组：73，75，78
实验组：68，69，80，76，82

解题思路：T检验或Wilcox检验一般要求任意一组样本量均大于等于5较为合适，且两组样本量相差较小（非平衡数据）。该问题样本量较小，普通的假设检验不适合，可以采用置换检验（两组平均值的差值作为统计量）。具体步骤：

第一步，零假设是实验组和对照组没有任何差别；
第二步，获取原始统计量。先计算两组平均值的差值作为统计量， $M_{0} = 0.333$ ；
第三步，对照组和实验组混合后随机抽取样本组成A和B再计算两组平均值的差值，重复该过程1000次，上述1000次得到的数值组成统计量分布 $M_{1000}$ ；
第四步，计算 $M_{1000}$ 大于 $M_{0} = 0.333$ 的个数 $n$ ，概率 $P = n /1000$ 。若 $P < 0.05$ 则说明实验处理有助于提升结果，否则接受零假设。

自己撰写脚本

control <- c(73, 75, 78)
treatment <- c(68, 69, 80, 76, 82)

permute_fun <- function(x1, x2, times = 1000) {
  
  # x1 = control
  # x2 = treatment
  # times = 1000
  
  M0 <- mean(x1) - mean(x2)
  x <- c(x1, x2)
  
  M_distri <- c()
  for (i in 1:times ) {
    x1_new <- sample(x, length(x1))
    x2_new <- sample(x, length(x2))
    
    M_temp <- mean(x1_new) - mean(x2_new)
    M_distri <- c(M_distri, M_temp)
  }
  
  dat <- data.frame(Time = 1:times,
                    Value = M_distri)
  p_value <- length(M_distri[M_distri > M0]) / length(M_distri)
  p_label <- paste0("Pvalue = ", p_value, " (M1000 > M0)")
  
  pl <- ggplot(dat, aes(x = Value)) + 
    geom_histogram(aes(y=..density..), binwidth=.5, 
                   color = "black", fill = "white") +
    geom_density(alpha=.2, fill="#FF6666") +
    scale_x_continuous(expand = c(0, 0)) +
    scale_y_continuous(expand = c(0, 0)) +
    labs(title = "Distribution of M statistics",
         x = "Mean(group1) - Mean(group2)") +
    geom_vline(xintercept = M0, color = "red", linetype = "dashed", linewidth = 1) +  
    annotate("text", label = p_label, x = 4, y = 0.14, size = 4) +
    theme_bw()
  
  return(pl)
}

permute_fun(x1 = control, x2 = treatment)

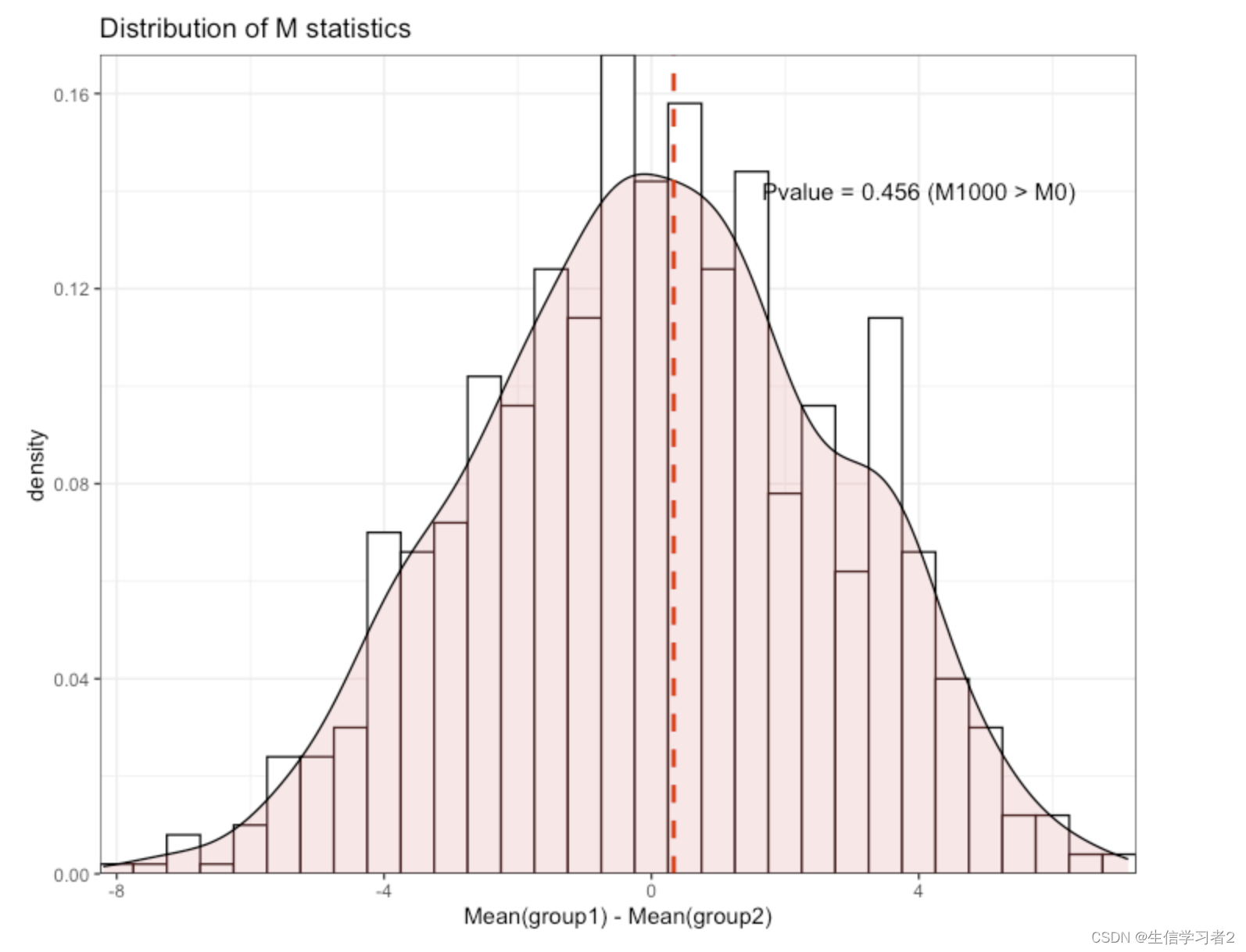
在这里插入图片描述

结果：Pvalue > 0.05，说明实验处理对结果没有显著提升。

内置函数

除了自己撰写脚本外，还可以通过R包内置的函数实现两组置换检验。

EnvStats::twoSamplePermutationTestLocation(
  x = control,
  y = treatment,
  fcn = 'mean',
  alternative = 'greater',
  mu1.minus.mu2 = 0,
  paired = FALSE,
  exact = FALSE,
  n.permutations = 1000,
  seed = 123)

Results of Hypothesis Test
--------------------------

Null Hypothesis:                 mu.x-mu.y = 0

Alternative Hypothesis:          True mu.x-mu.y is greater than 0

Test Name:                       Two-Sample Permutation Test
                                 Based on Differences in Means
                                 (Based on Sampling
                                 Permutation Distribution
                                 1000 Times)

Estimated Parameter(s):          mean of x = 75.33333
                                 mean of y = 75.00000

Data:                            x = control  
                                 y = treatment

Sample Sizes:                    nx = 3
                                 ny = 5

Test Statistic:                  mean.x - mean.y = 0.3333333

P-value:                         0.497

结果：Pvalue > 0.05，说明实验处理对结果没有显著提升。