高斯信道下通信感知一体化的性能极限(刘凡)
文章目录
-
- 背景


背景

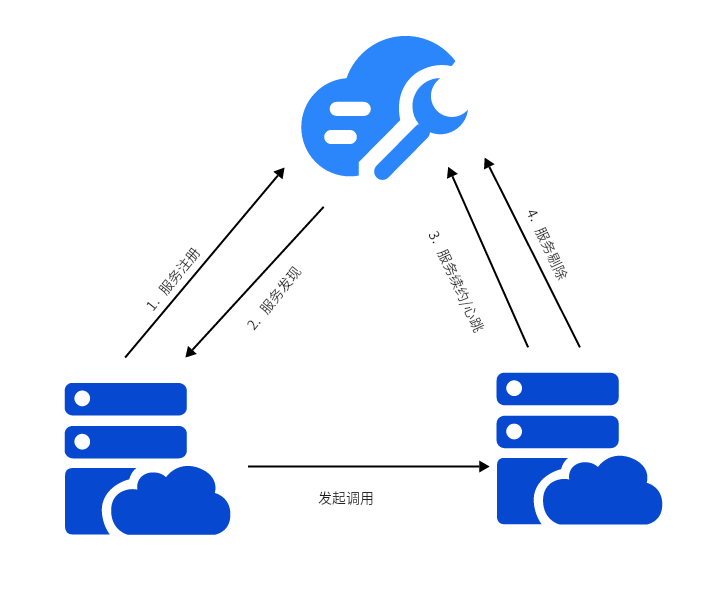
通信和感知在硬件结构上相似,高效地利用资源,实现相互的增益;

感知是基于不同的任务,比如目标检测(检测概率,虚警概率),估计任务(从收到的信号中去估计有用的参数,均方误差,CRB),识别(知道目标的语义信息,就是目标分类,识别准确率),这些感知指标基本都是可靠性指标,感知的结果难以量化成一个比特,所以我们不去讨论感知的有效性。

考虑估计指标,估计参数, E { ( η − η ^ ) ( η − η ^ ) T } ⩾ J − 1 = { E [ ∂ 2 ln p ( Y , η ) ∂ η ∂ η T ] } − 1 \mathbb{E}\Big\{(\mathbf{\eta}-\mathbf{\hat{\eta}})(\mathbf{\eta}-\mathbf{\hat{\eta}})^{\mathrm{T}}\Big\}\geqslant\mathbf{J}^{-1}=\Big\{\mathbb{E}\left[\frac{\partial^{2}\ln p(\mathbf{Y},\mathbf{\eta})}{\partial\mathbf{\eta}\partial\mathbf{\eta}^{\mathrm{T}}}\right]\Big\}^{-1} E{
(η−η^)(η−η^)T}⩾J−1={
E[∂η∂ηT∂2lnp(Y,η)]}−1,估计的参数是 η \eta η(比如距离、速度和角度等),比如发射一个信号打到一个目标上,返回的信号就携带了关于这个目标信息。信号记作 Y \mathbf{Y} Y,服从一定概率的随机变量, η \eta η也是随机变量(列向量),拿到 Y \mathbf{Y} Y对 η \eta η作估计,记作 η ^ \hat{\eta} η^, 求MSE即 E { ( η − η ^ ) ( η − η ^ ) T } \mathbb{E}\Big\{(\mathbf{\eta}-\mathbf{\hat{\eta}})(\mathbf{\eta}-\mathbf{\hat{\eta}})^{\mathrm{T}}\Big\} E{
(η−η^)(η−η^)T},统计里MSE有下界,下界就是CRB(CRB是感知的性能极限),CRB的PDF越尖,包含目标的信息就越多,它的逆就是误差的bound(CRB的PDF多尖定义为Fisher Information,Fisher Information是联合分布 p ( Y , η ) p(\mathbf{Y},\mathbf{\eta}) p(Y,η),为什么是联合分布,这是一个贝叶斯的CRB),联合分布 p ( Y , η ) p(\mathbf{Y},\mathbf{\eta}) p(Y,η)对 η ) \mathbf{\eta}) η)求二阶导取期望, [ ∂ 2 ln p ( Y , η ) ∂ η ∂ η T ] \left[\frac{\partial^{2}\ln p(\mathbf{Y},\mathbf{\eta})}{\partial\mathbf{\eta}\partial\mathbf{\eta}^{\mathrm{T}}}\right] [∂η∂ηT∂2lnp(Y,η)]叫Hessian矩阵(海森矩阵,Hessian矩阵求期望就是Fisher信息矩阵),海森矩阵求期望再取逆叫做CRB matrix,矩阵 { ( η − η ^ ) ( η − η ^ ) T } \Big\{(\mathbf{\eta}-\mathbf{\hat{\eta}})(\mathbf{\eta}-\mathbf{\hat{\eta}})^{\mathrm{T}}\Big\} {
(η−η^)(η−η^)T}在半正定意义上大于等于Hessian矩阵的逆,对 { ( η − η ^ ) ( η − η ^ ) T } \Big\{(\mathbf{\eta}-\mathbf{\hat{\eta}})(\mathbf{\eta}-\mathbf{\hat{\eta}})^{\mathrm{T}}\Big\} {
(η−η^)(η−η^)T}求迹tra,将所有误差加起来,CRB一般是 { E [ ∂ 2 ln p ( Y , η ) ∂ η ∂ η T ] } − 1 \Big\{\mathbb{E}\left[\frac{\partial^{2}\ln p(\mathbf{Y},\mathbf{\eta})}{\partial\mathbf{\eta}\partial\mathbf{\eta}^{\mathrm{T}}}\right]\Big\}^{-1} {
E[∂η∂ηT∂2lnp(Y,η)]}−1求trace。
一般的CRB中 η \eta η是确定变量, p ( Y , η ) p(\mathbf{Y},\mathbf{\eta}) p(Y,η)会变成似然函数(可以这样理解,观测数据和参数的联合分布,当其中一个给定,为了使得PDF最大,去优化另外一个,都是优化似然函数)。
半正定 (positive semidefinite)矩阵表示一个对称矩阵,其所有特征值都非负。
这意味着,对于任意非意 x \mathfrak{x} x,都有:
x T ( E { ( η − η ^ ) ( η − η ^ ) T } − J − 1 ( η ) ) x ≥ 0 \mathbf{x}^T\left(\mathbb{E}\Big\{(\eta-\hat{\eta})(\eta-\hat{\eta})^\mathrm{T}\Big\}-\mathbf{J}^{-1}(\eta)\Big)\mathbf{x}\geq0\right. xT(E{
(η−η^)(η−η^)T}−J−1(η))x≥0

下面讨论性能极限(通信人的传统),研究一个新的通信系统第一步先搞清楚性能极限,两个极限:速率和CRB,此时性能极限就不是一个点了,而是一个边界,相当于2元的优化问题。速率和CRB如果同时达到最优(CRB最小,Rate达到最大,为Bound B矩形边界,意味着通信和感知之间没有任何矛盾),Bound A是Time sharing可以达到的界,最优的CRB在左下工作点概率是P1,最高的rate在右上工作点概率是P2,P1+P2=1,概率变化就可以得到Bound A直线,这条线叫做分时内界(time sharing inner bound),代表资源上通信和感知正交分配的情况(通信和感知没有共享资源)。一个比较实际的折中就是Bound C,通信和感知有一部分资源是共享的。

如何分配通信和感知的资源:通信和感知有不同的评价指标,对资源的分配和调度就有不同的侧重点。比如正交分配(在时间、频谱或者波束上分配通信和感知,时分、频分和空分)。另外是一体化波形,会得到Bound C,如何找到Bound C并且逼近。

找到这条界:ISAC信道分为3种,1)强耦合:通信的目标也是感知的目标;2)中度耦合:感知和通信分成两条径都被手机接受;3)弱耦合:通信和感知的两个目标在物理上隔得很远。三种耦合程度部分决定了边界的形状。

强耦合,抽象成两个subspace,两个subspace方向相同,朝一个方向打,通信和感知完全复用。中度耦合,复用就是各自的投影。弱耦合,两个空间正交,不得不正交分配资源,资源没办法复用。
如果考虑一个简单的beamforming问题,对于某个目标角度的CRB的优化,通信速率满足一个门限和一个功率的约束。


向量高斯信道,MIMO或者OFDM信道。
感知接收机和发射机是否分开:
自发自收,一个通信用户,一个或者多个Target,ISAC的发射机,感知接收机。
发和收分开,但是中间可以用光纤连接,接受合作。
Y c = H c X + Z c , Y s = H s ( η ) X + Z s \mathbf{Y}_\mathrm{c}=\mathbf{H}_\mathrm{c}\mathbf{X}+\mathbf{Z}_\mathrm{c},\mathbf{Y}_\mathrm{s}=\mathbf{H}_\mathrm{s}(\mathbf{\eta})\mathbf{X}+\mathbf{Z}_\mathrm{s} Yc=HcX+Zc,Ys=Hs(η)X+Zs其中 Y c \mathbf{Y}_\mathrm{c} Yc是通信接收信号, Y s \mathbf{Y}_\mathrm{s} Ys是感知接收信号; X \mathbf{X} X是一个unified waveform,随机变量(只有随机信号才能携带信息);样本协方差矩阵,假设有N个天线,一个block的长度是T, X \mathbf{X} X就是一个N×T的矩阵(或者对应OFDM中N个OFDM符号,每个符号有T个子载波), X \mathbf{X} X的共轭转置/T就是样本协方差矩阵;求期望就是统计协方差矩阵。

一些重要的假设:
雷达的感知,感知的目标不能发射信号;
ISAC信号 X \mathbf{X} X对于感知接收机是已知的,因为在自发自收和发和收分开两种场景下,都是连接的。但是对通信接收机是未知的。
η \mathbf{\eta} η是IId,每T个symbol,iid地变化一次。
通信的channel, H c \mathbf{H}_\mathrm{c}