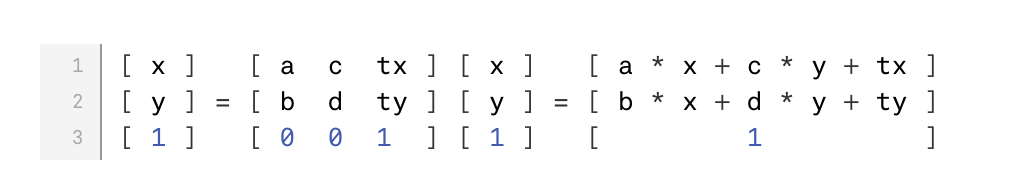🎯要点
🎯任意维度求解器,绘制三维投影结果 | 🎯解二维静电场、静磁场 | 🎯狄利克雷、诺依曼条件几何矩阵算子 | 🎯算法模拟低溫半导体材料 | 🎯计算曲面达西流 | 🎯电子结构计算和原子模拟 | 🎯算法模拟量子波函数和电子束
📜泊松方程 | 本文 - 用例
📜Python火焰锋动力学和浅水表面波浪偏微分方程
📜Python数值和符号算法计算及3D视图物理数学波形方程
📜Python射频电磁肿瘤热疗数学模型和电磁爆炸性变化统计推理模型
📜达西流用例:Python和R水力电导率和达西流神经算子


🍇Python最低阶有限差分泊松方程
我们想要解泊松方程:
∂
2
u
∂
x
2
+
∂
2
u
∂
y
2
=
0
\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0
∂x2∂2u+∂y2∂2u=0
在
[
0
,
1
]
×
[
0
,
1
]
[0,1] \times[0,1]
[0,1]×[0,1] 方域中,具有边界条件
u
(
x
,
0
)
=
x
,
u
(
x
,
1
)
=
x
−
1
,
u
(
0
,
y
)
=
−
y
,
u
(
1
,
y
)
=
1
−
y
.
u(x, 0)=x, \quad u(x, 1)=x-1, \quad u(0, y)=-y, \quad u(1, y)=1-y .
u(x,0)=x,u(x,1)=x−1,u(0,y)=−y,u(1,y)=1−y.
我们将使用最低阶有限差分表示:
∂
2
u
∂
x
2
(
x
i
,
y
j
)
≃
1
Δ
x
(
∂
u
∂
x
(
x
i
+
1
,
y
j
)
−
∂
u
∂
x
(
x
i
−
1
,
y
j
)
)
≃
1
Δ
x
(
1
Δ
x
(
u
(
x
i
+
1
,
y
j
)
−
u
(
x
i
,
y
j
)
)
−
1
Δ
x
(
u
(
x
i
,
y
j
)
−
u
(
x
i
−
1
,
y
j
)
)
)
\begin{gathered} \frac{\partial^2 u}{\partial x^2}\left(x_i, y_j\right) \simeq \frac{1}{\Delta x}\left(\frac{\partial u}{\partial x}\left(x_{i+1}, y_j\right)-\frac{\partial u}{\partial x}\left(x_{i-1}, y_j\right)\right) \\ \simeq \frac{1}{\Delta x}\left(\frac{1}{\Delta x}\left(u\left(x_{i+1}, y_j\right)-u\left(x_i, y_j\right)\right)-\frac{1}{\Delta x}\left(u\left(x_i, y_j\right)-u\left(x_{i-1}, y_j\right)\right)\right) \end{gathered}
∂x2∂2u(xi,yj)≃Δx1(∂x∂u(xi+1,yj)−∂x∂u(xi−1,yj))≃Δx1(Δx1(u(xi+1,yj)−u(xi,yj))−Δx1(u(xi,yj)−u(xi−1,yj)))
📜有限差分用例:Python微磁学磁倾斜和西塔规则算法
最终简化为,
∂
2
u
∂
x
2
+
∂
2
u
∂
y
2
≃
(
1
Δ
2
(
u
i
+
1
,
j
+
u
i
−
1
,
j
+
u
i
,
j
+
1
+
u
i
,
j
−
1
−
4
u
i
,
j
)
)
\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \simeq\left(\frac{1}{\Delta^2}\left(u_{i+1, j}+u_{i-1, j}+u_{i, j+1}+u_{i, j-1}-4 u_{i, j}\right)\right)
∂x2∂2u+∂y2∂2u≃(Δ21(ui+1,j+ui−1,j+ui,j+1+ui,j−1−4ui,j))
最直接的方法是直接求解线性系统:
import numpy as np
import matplotlib as ml
import matplotlib.pyplot as pp
def boundary(grid):
x = np.linspace(0,1,len(grid))
grid[0,:] = np.interp(x,[0,1],[0,1])
grid[:,-1] = np.interp(x,[0,1],[1,0])
grid[-1,:] = np.interp(x,[0,1],[-1,0])
grid[:,0] = np.interp(x,[0,1],[0,-1])
def poisson_direct(gridsize,set_boundary):
A = np.zeros(shape=(gridsize,gridsize,gridsize,gridsize),dtype='d')
b = np.zeros(shape=(gridsize,gridsize),dtype='d')
dx = 1.0 / (gridsize - 1)
for i in range(1,gridsize-1):
for j in range(1,gridsize-1):
A[i,j,i-1,j] = A[i,j,i+1,j] = A[i,j,i,j-1] = A[i,j,i,j+1] = 1/dx**2
A[i,j,i,j] = -4/dx**2
for i in range(0,gridsize):
A[0,i,0,i] = A[-1,i,-1,i] = A[i,0,i,0] = A[i,-1,i,-1] = 1
set_boundary(b)
return np.linalg.tensorsolve(A,b)
sol = poisson_direct(25,boundary)
为了展示解,我们需要将矩阵的通常解释(行、列、从上到左)与在笛卡尔平面上绘图的想法联系起来。
pp.imshow(sol.T,cmap=ml.cm.Blues,interpolation='none',origin='lower')
将其变成我们将再次使用的函数。
def showsol(sol):
pp.imshow(sol.T,cmap=ml.cm.Blues,interpolation='none',origin='lower')
showsol(poisson_direct(51,boundary))
让我们尝试一种迭代方法:我们将泊松方程转化为扩散方程来求解
∂
u
∂
t
=
∂
2
u
∂
x
2
+
∂
2
u
∂
y
2
\frac{\partial u}{\partial t}=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}
∂t∂u=∂x2∂2u+∂y2∂2u
并通过正向时间中心空间差分求解收敛
u
i
,
j
n
+
1
=
u
i
,
j
n
+
Δ
t
Δ
2
(
u
i
+
1
,
j
n
+
u
i
−
1
,
j
n
+
u
i
,
j
+
1
n
+
u
i
,
j
−
1
n
−
4
u
i
,
j
n
)
u_{i, j}^{n+1}=u_{i, j}^n+\frac{\Delta t}{\Delta^2}\left(u_{i+1, j}^n+u_{i-1, j}^n+u_{i, j+1}^n+u_{i, j-1}^n-4 u_{i, j}^n\right)
ui,jn+1=ui,jn+Δ2Δt(ui+1,jn+ui−1,jn+ui,j+1n+ui,j−1n−4ui,jn)
对于最大稳定时间步
Δ
t
=
Δ
2
/
4
\Delta t=\Delta^2 / 4
Δt=Δ2/4 ,导出雅可比方法
u
i
,
j
n
+
1
=
1
4
(
u
i
+
1
,
j
n
+
u
i
−
1
,
j
n
+
u
i
,
j
+
1
n
+
u
i
,
j
−
1
n
)
u_{i, j}^{n+1}=\frac{1}{4}\left(u_{i+1, j}^n+u_{i-1, j}^n+u_{i, j+1}^n+u_{i, j-1}^n\right)
ui,jn+1=41(ui+1,jn+ui−1,jn+ui,j+1n+ui,j−1n)
这相当于用最近邻的平均值替换每个网格值。这与调和函数理论是一致的。
def jacobi(grid):
newgrid = np.zeros(shape=grid.shape,dtype=grid.dtype)
newgrid[1:-1,1:-1] = 0.25 * (grid[1:-1,:-2] + grid[1:-1,2:] +
grid[:-2,1:-1] + grid[2:,1:-1])
newgrid[0,:] = grid[0,:]
newgrid[-1,:] = grid[-1,:]
newgrid[:,0] = grid[:,0]
newgrid[:,-1] = grid[:,-1]
return newgrid
我们从随机配置开始,应用边界条件,然后迭代。我们间歇性地绘制解,结果显示它收敛了。