拓扑排序(Topological Sorting)是一种用于有向无环图(DAG)的排序算法,其输出是图中所有顶点的线性排序,使得对于每条有向边 (u, v),顶点 u 在 v 之前出现。拓扑排序确定了项目网络图中的起始事件和终止事件,也就是顶点的执行顺序。
因为是有向无环图,所以拓扑排序的作用其实就是把先发生的排序在前面,后发生的排序到后面。
例如现在我们有一个有向无环图:

我们可以发现,先发生的是入度为0的顶点,也就是没有边指向的顶点,此时该顶点不需要考虑自己的前驱是否发生完,所以是先发生的顶点,例如顶点 0 和顶点 5 ,这时我们取出这两个顶点,证明已经发生完。

此时只在考虑谁的入度为0,此时顶点 3 和顶点 2 的入度都为0,所以取出这两个顶点,最后只剩下顶点 1 和顶点 4 。
那么我们该如何实现这个过程呢,首先要注意边数组的输入:

这里,1 表示该顶点指向另一个顶点,0 则表示没有边。
接下来我们来思考一下代码的思路:
1.计算每个顶点的入度,
2.如果入度为 0 ,记录该顶点,输出。
3.拿到入度为 0 的顶点,并且把该顶点的边都删除掉。
4.重新计算入度,重复第2步,第3步操作。
这里我们如果要记录该顶点,可以使用队列或者栈,都可以,就拿一开始入度为0的顶点 0 和顶点 5 来说,队列的话会输出 0 5,而栈会输出 5 0 ,两者都可以,这里用栈举例子。
首先是入度数组的初始化:
int* inDegrees = (int*)malloc(sizeof(int) * G->vexsNum);
for (int i = 0; i < G->vexsNum; i++) {
inDegrees[i] = 0;
}
for (int i = 0; i < G->vexsNum; i++) {
for (int j = 0; j < G->vexsNum; j++) {
if (G->arcs[i][j]) {
inDegrees[j]++;
}
}
}if (G->arcs[i][j]) inDegrees[j]++;也就是如果有指向该顶点的边,该顶点的入度就加1。
接下来后三步操作:
for (int i = 0; i < G->vexsNum; i++) {
if (inDegrees[i] == 0) {
StackPush(S, i);
}
}
while (!IsEmpty(S)) {
int index = StackPop(S);
printf("%c ", G->vexs[index]);
for (int i = 0; i < G->vexsNum; i++) {
if (G->arcs[index][i]) {
inDegrees[i]--;
if (inDegrees[i] == 0) {
StackPush(S, i);
}
}
}
}首先第一个for循环是让入度为0的顶点入栈,然后while循环,出栈拿到入度为0的顶点序号index,接着如果该顶点有指向其他顶点的边 if (G->arcs[index][i]) ,那么就让其他顶点的入度减1,最后再判断一下,如果更新后的入度数组有为 0 的,就将该数组入栈,继续循环。
把两部分组合起来:
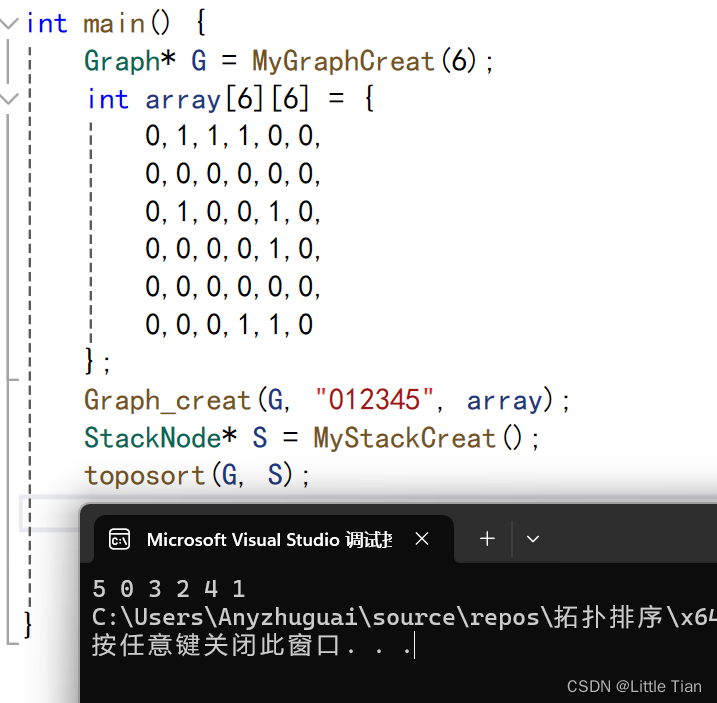
void toposort(Graph* G,StackNode* S) {
int* inDegrees = (int*)malloc(sizeof(int) * G->vexsNum);
for (int i = 0; i < G->vexsNum; i++) {
inDegrees[i] = 0;
}
for (int i = 0; i < G->vexsNum; i++) {
for (int j = 0; j < G->vexsNum; j++) {
if (G->arcs[i][j]) {
inDegrees[j]++;
}
}
}
for (int i = 0; i < G->vexsNum; i++) {
if (inDegrees[i] == 0) {
StackPush(S, i);
}
}
while (!IsEmpty(S)) {
int index = StackPop(S);
printf("%c ", G->vexs[index]);
for (int i = 0; i < G->vexsNum; i++) {
if (G->arcs[index][i]) {
inDegrees[i]--;
if (inDegrees[i] == 0) {
StackPush(S, i);
}
}
}
}
}
这就是文章的全部内容了,希望对你有所帮助,如有错误欢迎评论。