本文使用 PINN解偏微分方程实例1中展示的代码求解了以四个具体的偏微分方程，包括Diffusion，Burgers, Allen–Cahn和Wave方程，另外重新写了一个求解反问题的代码，以burger方程为例。

一、正问题

1. Diffusion equation

一维扩散方程:
$$\begin{array}{l}\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}+e^{-t}\left(-\sin (\pi x)+{\pi }^2\sin (\pi x)\right),x\in [-1,1],t\in [0,1]\\ u(x,0)=\sin (\pi x)\\ u(-1,t)=u(1,t)=0\end{array}$$
其中 $u$ 是扩散物质的浓度。精确解是 $u(x,t)=sin(\pi x)e^{-t}$ 表示。

2. Burgers’ equation

Burgers方程的定义为：
$$\begin{array}{l}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=v\frac{{\partial }^{2}u}{\partial x^2},x\in [-1,1],t\in [0,1],\\ u(x,0)=-\sin (\pi x),\\ u(-1,t)=u(1,t)=0,\end{array}$$
其中，$u$ 为流速，$\nu$ 为流体的粘度。在本文中，$\nu$ 设为 $0.01/\pi$。

3. Allen–Cahn equation

Allen–Cahn方程的形式如下:
$$\begin{array}{l}\frac{\partial u}{\partial t}=D\frac{{\partial }^{2}u}{\partial x^2}+5\left(u-u^3\right),x\in [-1,1],t\in [0,1],\\ u(x,0)=x^2\cos (\pi x),\\ u(-1,t)=u(1,t)=-1,\end{array}$$
其中，扩散系数 $D=0.001$ .

4. Wave equation

一维波动方程如下：
$$\begin{array}{l}\frac{{\partial }^{2}u}{\partial t^2}-4\frac{{\partial }^{2}u}{\partial x^2}=0,x\in [0,1],t\in [0,1],\\ u(0,t)=u(1,t)=0,t\in [0,1],\\ u(x,0)=\sin (\pi x)+\frac{1}{2}\sin (4\pi x),x\in [0,1],\\ \frac{\partial u}{\partial t}(x,0)=0,x\in [0,1],\end{array}$$
精确解为：
$$u(x,t)=\sin (\pi x)\cos (2\pi t)+\frac{1}{2}\sin (4\pi x)\cos (8\pi t).$$

二、反问题

1. Burgers’ equation

Burgers方程的定义为：
$$\begin{array}{l}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=v\frac{{\partial }^{2}u}{\partial x^2},x\in [-1,1],t\in [0,1],\\ u(x,0)=-\sin (\pi x),\\ u(-1,t)=u(1,t)=0,\end{array}$$
其中，$u$ 为流速，$\nu$ 为流体的粘度。
  这里假设 $v$ 未知，我们同时求解方程的解和v的值。

3. 部分代码示例

import torch
import numpy as np
import matplotlib.pyplot as plt

sin = torch.sin
cos = torch.cos
exp = torch.exp
pi = torch.pi

epochs = 50000    # 训练代数,要为1000的整数倍
h = 100    # 画图网格密度
N = 30    # 内点配置点数
N1 = 10    # 边界点配置点数
N2 = 5000    # 数据点

# error
L2_error = []
L2_error_data = []
L2_error_eq = []
# Training
u = MLP()
opt = torch.optim.Adam(params=u.parameters())
xt, u_real = test_data(x_inf=-1, x_sup=1, t_inf=0, t_sup=1, h=h)
print("**************** equation+data ********************")
for i in range(epochs):
    opt.zero_grad()
    l = l_interior(u) \
        + l_down(u) \
        + l_left(u) \
        + l_right(u) \
        + l_data(u)
    l.backward()
    opt.step()
    if (i+1) % 1000 == 0 or i == 0:
        u_pred = u(xt)
        error = l2_relative_error(u_real, u_pred.detach().numpy())
        L2_error.append(error)
        print("L2相对误差: ", error)


u1 = MLP()
opt = torch.optim.Adam(params=u1.parameters())
print("**************** data ********************")
for i in range(epochs):
    opt.zero_grad()
    l = l_data(u1)
    l.backward()
    opt.step()
    if (i+1) % 1000 == 0 or i == 0:
        u_pred = u1(xt)
        error = l2_relative_error(u_real, u_pred.detach().numpy())
        L2_error_data.append(error)
        print("L2相对误差: ", error)


u2 = MLP()
opt = torch.optim.Adam(params=u2.parameters())
print("**************** equation ********************")
for i in range(epochs):
    opt.zero_grad()
    l = l_interior(u2) \
        + l_down(u2) \
        + l_left(u2) \
        + l_right(u2)
    l.backward()
    opt.step()
    if (i+1) % 1000 == 0 or i == 0:
        u_pred = u2(xt)
        error = l2_relative_error(u_real, u_pred.detach().numpy())
        L2_error_eq.append(error)
        print("L2相对误差: ", error)


print("********************************")
print("PINN相对误差为: ", L2_error[-1])
print("equation相对误差为: ", L2_error_eq[-1])
print("data相对误差为: ", L2_error_data[-1])
print("********************************")

x = range(int(epochs / 1000 + 1))
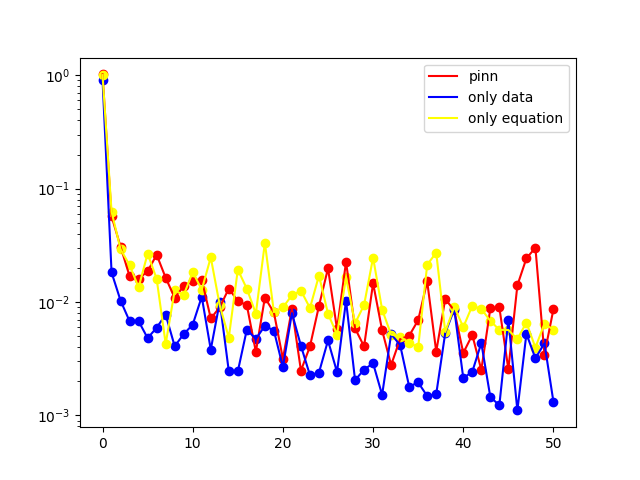
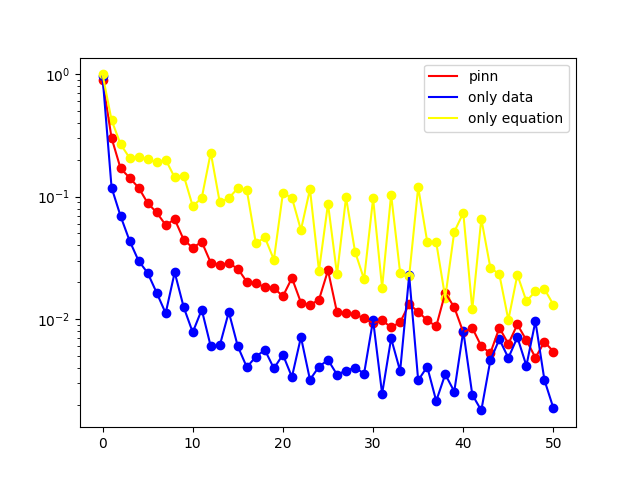
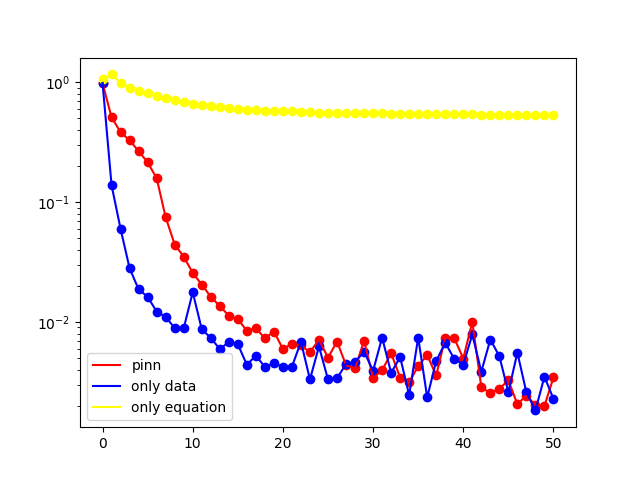
plt.plot(x, L2_error, c='red', label='pinn')
plt.plot(x, L2_error_data, c='blue', label='only data')
plt.plot(x, L2_error_eq, c='yellow', label='only equation')
plt.scatter(x, L2_error, c='red')
plt.scatter(x, L2_error_data, c='blue')
plt.scatter(x, L2_error_eq, c='yellow')
plt.yscale('log')
plt.legend()
plt.show()

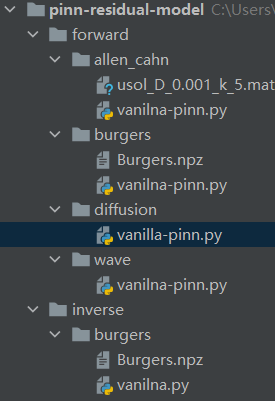
完整代码目录如下：