🌈🌈😄😄
欢迎来到茶色岛独家岛屿，本期将为大家揭晓LeetCode 46. 全排列 51. N 皇后 52. N皇后 II，做好准备了么，那么开始吧。
🌲🌲🐴🐴
46. 全排列
一、力扣示例
二、解决办法
三、代码实现
51. N 皇后
一、力扣示例
二、解决办法
三、代码实现
52. N皇后 II
一、力扣示例
二、解决办法
三、代码实现
其实回溯算法和我们常说的 DFS 算法非常类似，本质上就是一种暴力穷举算法。回溯算法和 DFS 算法的细微差别是：回溯算法是在遍历「树枝」，DFS 算法是在遍历「节点」
回溯算法的这段核心框架
解决一个回溯问题，实际上就是一个决策树的遍历过程，站在回溯树的一个节点上，你只需要思考 3 个问题：
1、路径：也就是已经做出的选择。
2、选择列表：也就是你当前可以做的选择。
3、结束条件：也就是到达决策树底层，无法再做选择的条件。
下面用几道例题演示一下
46. 全排列
一、力扣示例
46. 全排列 - 力扣（LeetCode）
https://leetcode.cn/problems/permutations/
二、解决办法
回溯
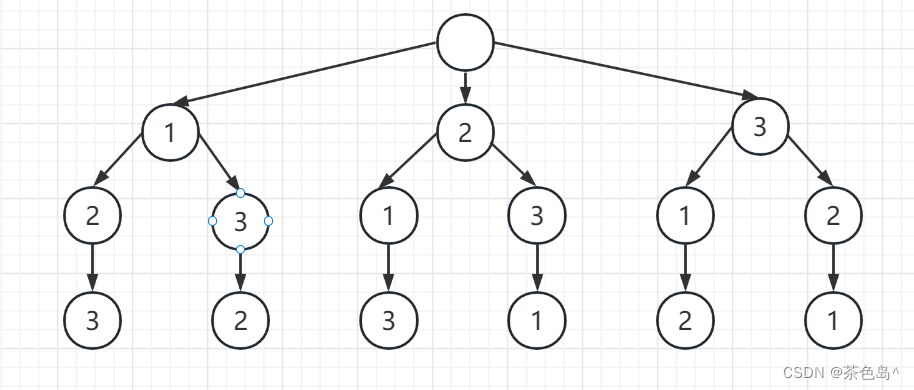
[2] 就是「路径」，记录你已经做过的选择；[1,3] 就是「选择列表」，表示你当前可以做出的选择；「结束条件」就是遍历到树的底层叶子节点，这里也就是选择列表为空的时候。
运用回溯框架，即可解决此题。
三、代码实现
class Solution {
List<List<Integer>> res = new LinkedList<>();
/* 主函数，输入一组不重复的数字，返回它们的全排列 */
List<List<Integer>> permute(int[] nums) {
// 记录「路径」
LinkedList<Integer> track = new LinkedList<>();
// 「路径」中的元素会被标记为 true，避免重复使用
//初始化路径为false，当路径被标记设为true
boolean[] used = new boolean[nums.length];
backtrack(nums, track, used);
return res;
}
// 路径：记录在 track 中
// 选择列表：nums 中不存在于 track 的那些元素（used[i] 为 false）
// 结束条件：nums 中的元素全都在 track 中出现
void backtrack(int[] nums, LinkedList<Integer> track, boolean[] used) {
// 触发结束条件
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
// 排除不合法的选择
if (used[i]) {
// nums[i] 已经在 track 中，跳过
continue;
}
// 做选择
track.add(nums[i]);
used[i] = true;
// 进入下一层决策树
backtrack(nums, track, used);
// 取消选择
track.removeLast();
used[i] = false;
}
}
}
51. N 皇后
一、力扣示例
51. N 皇后 - 力扣（LeetCode）https://leetcode.cn/problems/n-queens/
二、解决办法
回溯
找寻
1、路径：也就是已经做出的选择。
2、选择列表：也就是你当前可以做的选择。
3、结束条件：也就是到达决策树底层，无法再做选择的条件。
运用回溯框架，求解此题
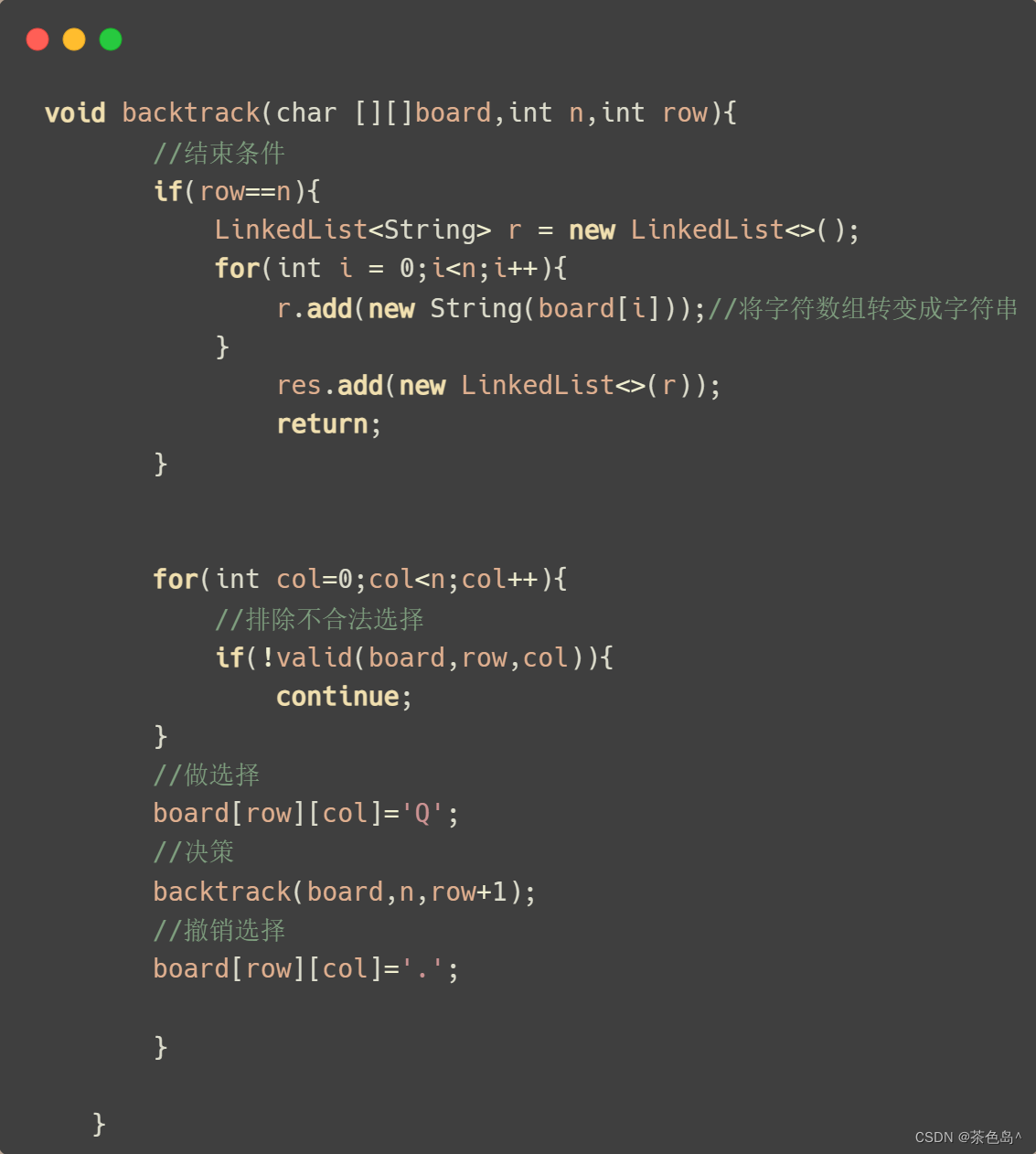
三、代码实现
class Solution {
List<List<String>> res=new LinkedList<>();
public List<List<String>> solveNQueens(int n) {
char [][]board=new char [n][n];
for(int i=0;i<n;i++){
Arrays.fill(board[i],'.');//将二维字符数组每位数赋值为字符'.'
}
backtrack(board,n,0);//调用函数求每个满足的排法
return res;
}
void backtrack(char [][]board,int n,int row){
//结束条件
if(row==n){
LinkedList<String> r = new LinkedList<>();
for(int i = 0;i<n;i++){
r.add(new String(board[i]));//将字符数组转变成字符串
}
res.add(new LinkedList<>(r));
return;
}
for(int col=0;col<n;col++){
//排除不合法选择
if(!valid(board,row,col)){
continue;
}
//做选择
board[row][col]='Q';
//决策
backtrack(board,n,row+1);
//撤销选择
board[row][col]='.';
}
}
boolean valid(char [][]board,int row,int col){
int n = board.length;
// 检查列是否有皇后互相冲突
for (int i = 0; i <= row; i++) {
if (board[i][col] == 'Q')
return false;
}
// 检查右上方是否有皇后互相冲突
for (int i = row - 1, j = col + 1;
i >= 0 && j < n; i--, j++) {
if (board[i][j] == 'Q')
return false;
}
// 检查左上方是否有皇后互相冲突
for (int i = row - 1, j = col - 1;
i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q')
return false;
}
return true;
}
}
52. N皇后 II
一、力扣示例
52. N皇后 II - 力扣（LeetCode）https://leetcode.cn/problems/n-queens-ii/
二、解决办法
回溯
此解和N皇后类似，只是不需要将解求出来，而是计算解的个数。
三、代码实现
class Solution {
int count;
public int totalNQueens(int n) {
char [][]board=new char [n][n];
for(int i=0;i<n;i++){
Arrays.fill(board[i],'.');
}
backtrack(board, 0);
return count;
}
void backtrack(char [][]board,int row){
if(board.length==row){
count++;
return;
}
int n = board[row].length;
for(int col=0;col<n;col++){
if(!valid(board,row,col)){
continue;
}
board[row][col]='Q';
backtrack(board,row+1);
board[row][col]='.';
}
}
boolean valid(char [][]board,int row,int col){
int n = board.length;
// 检查列是否有皇后互相冲突
for (int i = 0; i <= row; i++) {
if (board[i][col] == 'Q')
return false;
}
// 检查右上方是否有皇后互相冲突
for (int i = row - 1, j = col + 1;
i >= 0 && j < n; i--, j++) {
if (board[i][j] == 'Q')
return false;
}
// 检查左上方是否有皇后互相冲突
for (int i = row - 1, j = col - 1;
i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q')
return false;
}
return true;
}
}
