本篇文章是博主在人工智能等领域学习时,用于个人学习、研究或者欣赏使用,并基于博主对人工智能等领域的一些理解而记录的学习摘录和笔记,若有不当和侵权之处,指出后将会立即改正,还望谅解。文章分类在AI学习笔记:
AI学习笔记(8)---《聚类算法(2)--- ISODATA算法》
聚类算法(2)--- ISODATA算法
目录
一、 ISODATA算法
1.1算法原理
1.2实验应用
二、 ISODATA算法python实现
2.1 算法流程
2.2 算法python程序
2.3 算法注意事项
三、 ISODATA算法实验结果
四、小结
一、 ISODATA算法
ISODATA算法(Iterative Self-Organizing Data Analysis Technique Algorithm)是一种经典的聚类算法,结合了K-均值和层次聚类的特点。该算法通过动态调整簇的数量和簇的中心点,能够根据数据特点自适应地调整聚类情况。
其他聚类算法见:
聚类算法(1)---最大最小距离、C-均值算法
1.1算法原理
SODATA算法采用迭代的方式动态地更新簇的数目和簇的中心,根据设定的参数来调整簇的数量以及样本点与簇之间的距离等。算法首先初始化聚类中心并对样本进行初步的分组,然后根据一定
1.2实验应用
ISODATA算法在实际应用中有着广泛的应用,特别是在数据挖掘、图像处理和生物信息学等领域。例如在地理信息系统(GIS)领域,ISODATA算法可以用于空间数据的聚类分析,对地理位置数据进行聚类,以实现地理空间上的模式识别和区域划分。
二、 ISODATA算法python实现
ISODATA(Iterative Self-Organizing Data Analysis Technique)算法是一种自组织数据分析技术,主要用于聚类分析。其算法流程如下:
2.1 算法流程
(1)初始化参数:选择初始的簇中心数量K、设定其他参数(如每个簇的最小样本数、簇内样本方差阈值等),并随机选择K个点作为初始的簇中心。
(2)分配样本:对于数据集中的每个样本点,计算它与各个簇中心的距离,并将其分配到距离最近的簇中。
(3)簇合并:检查每个簇的样本方差是否大于预设的阈值,如果是,则将该簇进行分裂,生成新的簇中心。
(4)簇分裂:重复执行步骤2和步骤3,直至满足终止条件(如簇中心不再发生大的变化、达到最大迭代次数等)。
(5)更新簇中心:根据当前的簇分配情况,重新计算每个簇中所有样本点的均值,以此更新簇中心的位置。
(6)重复迭代:重复执行步骤2至步骤5,直至满足终止条件(如簇中心不再发生大的变化、达到最大迭代次数等)。
(7)输出结果:得到K个簇,每个簇包含若干个样本点,完成聚类过程。
2.2 算法python程序
导入需要的python库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import euclidean_distances
import copyISODATA聚类算法
class ISODATA():
def __init__(self, designCenterNum, Nc, LeastSampleNum, StdThred, LeastCenterDist, L, iterationNum):
# 指定预期的聚类数、初始聚类中心个数、每类的最小样本数、标准差阈值、最小中心距离、每次可合并的最多对数、迭代次数
self.K = designCenterNum
self.centerNum = Nc
self.thetaN = LeastSampleNum
self.thetaS = StdThred
self.thetaC = LeastCenterDist
self.L = L
self.iteration = iterationNum
self.data = np.stack([[0, 0], [0, 1], [4, 4], [4, 5], [5, 4], [5, 5], [1, 0]], dtype=np.float64)
self.label = np.stack([0, 0, 0, 0, 0, 0, 0])
# 随机选取NC个初始聚类中心
center_ind = np.random.choice(np.arange(len(self.data), dtype=np.int32), Nc, replace=False)
self.center = np.stack([copy.deepcopy(self.data[center_ind[i], :]) for i in range(Nc)])
self.centerMeanDist = 0
# 更新
def updateLabel(self):
# 计算样本到中心的距离
distance = euclidean_distances(self.data, self.center.reshape((self.centerNum, -1)))
# 选出每个模式到各个中心的最小距离,并为样本重新分配标签
self.label = np.argmin(distance, 1)
for i in range(self.centerNum):
# 找出同一类样本
index = np.argwhere(self.label == i).squeeze()
sameClassSample = self.data[index, :]
# 更新中心
if len(sameClassSample.shape) >= 2:
self.center[i, :] = np.mean(sameClassSample, 0)
# 计算所有类到各自中心的平均距离之和
for i in range(self.centerNum):
# 找出同一类样本
index = np.argwhere(self.label == i).squeeze()
sameClassSample = self.data[index, :]
if len(sameClassSample.shape) < 2:
sameClassSample = sameClassSample.reshape((1,-1))
# 计算样本到中心距离的平均值
distance = np.mean(euclidean_distances(sameClassSample, self.center[i, :].reshape((1, -1))))
# 更新中心
self.centerMeanDist += distance
self.centerMeanDist /= self.centerNum
def divide(self):
# 临时保存更新后的中心集合,否则在删除和添加的过程中顺序会乱
newCenterSet = self.center
# 计算每个类的样本在每个维度的标准差
for i in range(self.centerNum):
# 找出同一类样本
index = np.argwhere(self.label == i).squeeze()
sameClassSample = self.data[index, :]
# 计算样本到中心每个维度的标准差
stdEachDim = np.mean((sameClassSample - self.center[i, :])**2, axis=0)
if type(stdEachDim) is not np.ndarray:
maxStd = stdEachDim
sameClassSample = sameClassSample.reshape(1,-1)
# 找出其中维度的最大标准差
else:
maxIndex = np.argmax(stdEachDim)
maxStd = stdEachDim[maxIndex]
# 计算样本到本类中心的距离
distance = np.mean(euclidean_distances(sameClassSample, self.center[i, :].reshape((1, -1))))
# 如果最大标准差超过了阈值
if maxStd > self.thetaS:
# 还需要该类的样本数大于于阈值很多 且 太分散才进行分裂
if self.centerNum <= self.K//2 or \
sameClassSample.shape[0] > 2 * (self.thetaN+1) and distance >= self.centerMeanDist:
newCenterFirst = self.center[i, :].copy()
newCenterSecond = self.center[i, :].copy()
newCenterFirst[maxIndex] += 0.5 * maxStd
newCenterSecond[maxIndex] -= 0.5 * maxStd
# 删除原始中心
newCenterSet = np.delete(newCenterSet, i, axis=0)
# 添加新中心
newCenterSet = np.vstack((newCenterSet, newCenterFirst))
newCenterSet = np.vstack((newCenterSet, newCenterSecond))
else:
continue
# 更新中心集合
self.center = newCenterSet
self.centerNum = self.center.shape[0]
def combine(self):
# 临时保存更新后的中心集合,否则在删除和添加的过程中顺序会乱
delIndexList = []
# 计算中心之间的距离
centerDist = euclidean_distances(self.center, self.center)
centerDist += (np.eye(self.centerNum)) * 10**10
# 把中心距离小于阈值的中心对找出来,每次和并数量少于L对
for i in range(self.L):
# 如果最小的中心距离都大于阈值的话,则不再进行合并
minDist = np.min(centerDist)
if minDist >= self.thetaC:
break
# 否则合并(两个中心距离太近合并)
index = np.argmin(centerDist)
row = index // self.centerNum
col = index % self.centerNum
# 找出合并的两个类别
index = np.argwhere(self.label == row)
classNumFirst = len(index)
index = np.argwhere(self.label == col)
classNumSecond = len(index)
newCenter = self.center[row, :] * (classNumFirst / (classNumFirst+ classNumSecond)) + \
self.center[col, :] * (classNumSecond / (classNumFirst+ classNumSecond))
# 记录被合并的中心
delIndexList.append(row)
delIndexList.append(col)
# 增加合并后的中心
self.center = np.vstack((self.center, newCenter))
self.centerNum -= 1
# 标记,以防下次选中
centerDist[row, :] = float("inf")
centerDist[col, :] = float("inf")
centerDist[:, col] = float("inf")
centerDist[:, row] = float("inf")
# 更新中心
self.center = np.delete(self.center, delIndexList, axis=0)
self.centerNum = self.center.shape[0]
def drawResult(self):
color = ['r', 'b', 'g', 'c', 'm', 'y']
ax = plt.gca()
ax.clear()
for i in range(self.centerNum):
index = np.argwhere(self.label == i).squeeze()
ax.scatter(self.data[index, 0], self.data[index, 1], c=color[i], label=f'Cluster { i}')
ax.scatter(self.center[i,0], self.center[i,1], c=color[i], marker='x',
label=f'Centroid { i}')
# ax.set_aspect(1)
# 坐标信息
plt.title('ISODATA Clustering')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
def start(self):
# 初始化中心和label
self.updateLabel()
self.drawResult()
# 到设定的次数自动退出
for i in range(self.iteration):
# 如果是偶数次迭代或者中心的数量太多,那么进行合并
if self.centerNum < self.K //2:
self.divide()
# 偶数次迭代或者中心数大于预期的一半,进行合并
elif (i > 0 and i % 2 == 0) or self.centerNum > 2 * self.K:
self.combine()
else:
self.divide()
# 更新中心
self.updateLabel()
print("中心数量:{}".format(self.centerNum))
self.drawResult()主函数
if __name__ == "__main__":
isoData = ISODATA(designCenterNum=2, Nc=3, LeastSampleNum=1, StdThred=0.1, LeastCenterDist=2, L=3, iterationNum=5)
isoData.start()2.3 算法注意事项
ISODATA算法相比于传统的K-means算法增加了簇合并和簇分裂的步骤,这使得算法能够动态地调整簇的数量和形状,适应数据的复杂性。在实际应用中,还可以根据具体情况对参数进行调整,以获得更好的聚类效果。
三、 ISODATA算法实验结果
相关参数设置:
| 参数类型 | 数值 |
| 预期的聚类数 | 2 |
| 初始聚类中心个数 | 3 |
| 每类的最小样本数 | 3 |
| 标准差阈值 | 0.1 |
| 最小中心距离 | 2 |
| 每次可合并的最多对数 | 3 |
| 迭代次数 | 5 |
(1)数据可视化聚类单步输出结果:

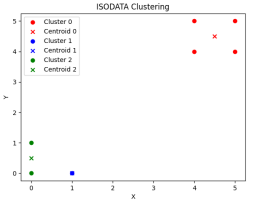
第一步 第二步
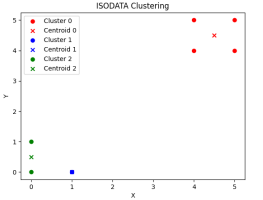

第三步 第四步
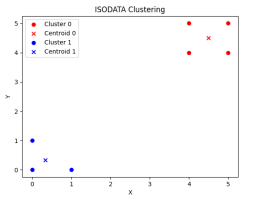
第五步
由多次实验结果可知,一般运行到五步以内即可达到聚类目的,合理设置相关参数可以达到满足聚类的要求。
(1)调整预期聚类数:
预期的聚类数=3时,
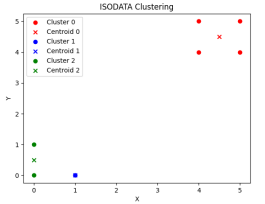
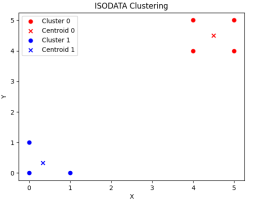
第一步运行结果 最终运行结果
预期的聚类数=5时,
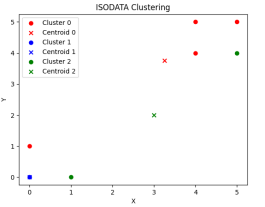
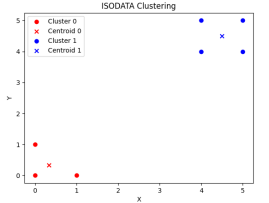
第一步运行结果 最终运行结果
由此实验可知,设置预期的聚类数为3或者5,聚类的最终结果分类为2类。后续经过多次其他预期的聚类数设置,得到结果聚类分类为2类,初步推算,预期聚类数的设置不影响最终聚类的结果。若修改其他参数,也可分析相应的实验输出结果。
四、小结
ISODATA算法是基于C-均值算法的改进,增加了簇的合并和分裂机制,使其能够动态地调整簇的数量和形状,适应数据的复杂性。这使得ISODATA算法更适用于数据集具有复杂形状、密度不均匀、簇的数量变化较大的情况。然而,对于该算法来说,需要合理设置参数,并且算法复杂度较高,需要更多的计算资源和时间。
通过合理选择算法、优化参数和评估结果,可以实现对提供的数据成功的进行聚类。在实际应用中,通常会根据具体情况综合考虑算法的优缺点,选择合适的算法,并不断优化参数,以获得满足实际需求的聚类效果。
文章若有不当和不正确之处,还望理解与指出。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请联系博主删除。如有错误、疑问和侵权,欢迎评论留言联系作者,或者私信联系作者。

![[最新教程]Claude Sonnet 3.5注册方法详细步骤分享,新手小白收藏,文末免费送已注册的Claude账号](https://img-blog.csdnimg.cn/direct/51b2662c022d4d52ac176913468160c1.png)