【技巧】Leetcode 201. 数字范围按位与【中等】

news2025/2/6 17:01:57

数字范围按位与

给你两个整数 left 和 right ，表示区间 [left, right] ，返回此区间内所有数字按位与的结果（包含 left 、right 端点）。

示例 1：

输入：left = 5, right = 7
输出：4

解题思路

在一个范围内进行按位与操作时，如果这个范围跨越了多个2的幂次方区间，那么最终的结果中，这些幂次方位上的所有位都将变为0。例如：

对于范围 [5, 7]，按位与的结果是 4，因为：
5 的二进制表示是 101
6 的二进制表示是 110
7 的二进制表示是 111
5 & 6 & 7 = 100 (即只有相同前缀的数字保留了，其他位都是0)

可以通过不断右移操作，找到左端点和右端点的共同前缀（非共同前缀&的结果一定是0），记录右移的次数，最后将共同前缀左移回原来的位置。

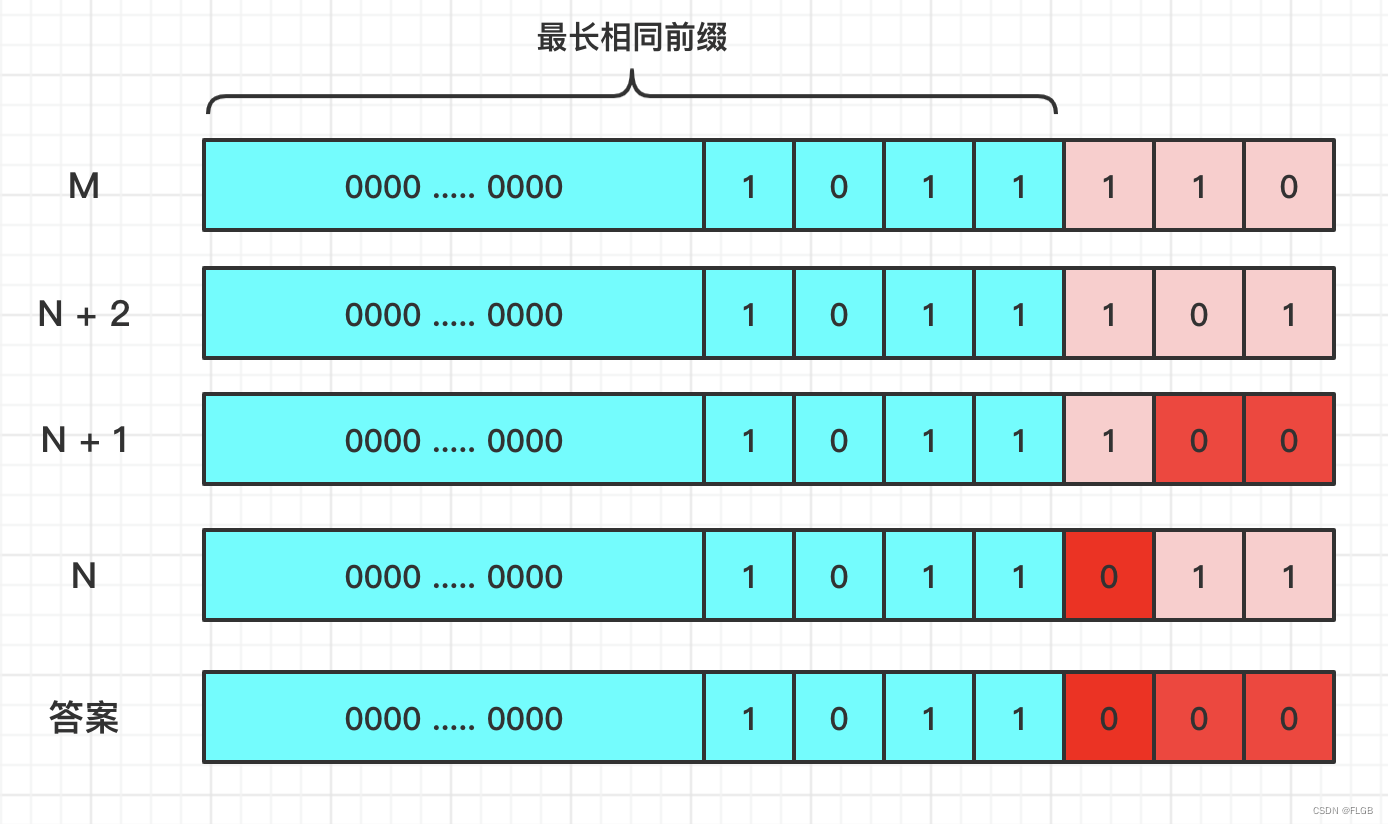
**例如：**n 和 m 的二进制及最长前缀如下图所示，后缀 011 累加到 110 必然经过 100。011 和 100 保证了答案中长度为 3 的后缀必然均为 0。
在这里插入图片描述

java实现

public class RangeBitwiseAnd {
    public int rangeBitwiseAnd(int left, int right) {
        int shift = 0;
        
        // 找到 left 和 right 的共同前缀
        while (left < right) {
            left >>= 1;
            right >>= 1;
            shift++;
        }
        
        // 将共同前缀左移回去
        return left << shift;
    }

    // 测试用例
    public static void main(String[] args) {
        RangeBitwiseAnd solution = new RangeBitwiseAnd();
        System.out.println(solution.rangeBitwiseAnd(5, 7)); // 期望输出: 4
        System.out.println(solution.rangeBitwiseAnd(0, 1)); // 期望输出: 0
        System.out.println(solution.rangeBitwiseAnd(1, 2147483647)); // 期望输出: 0
    }
}