目录

引言

1. 回归分析

1.1 线性回归

基本概念

Matlab实现

1.2 多元回归

基本概念

Matlab实现

1.3 非线性回归

基本概念

Matlab实现

2. 时间序列分析

2.1 时间序列的基本概念

2.2 移动平均

基本概念

Matlab实现

2.3 指数平滑

基本概念

Matlab实现

2.4 ARIMA模型

基本概念

Matlab实现

3. 优化模型

3.1 线性规划

基本概念

Matlab实现

3.2 非线性规划

基本概念

Matlab实现

4. 微分方程模型

4.1 常微分方程模型

基本概念

Matlab实现

4.2 偏微分方程模型

基本概念

Matlab实现

4.3 微分方程模型的应用案例

案例：传染病模型

结语

---

引言

在前两篇文章中，我们已经介绍了数学建模的基础知识和入门方法。本篇文章将深入讲解几种典型的数学建模方法，包括回归分析、时间序列分析、优化模型和微分方程模型。这些方法在实际问题中应用广泛，对于理解和解决复杂系统中的问题至关重要。通过详细的案例分析和Matlab代码示例，帮助读者掌握具体的建模技术。

1. 回归分析

1.1 线性回归

基本概念

线性回归用于建立因变量与一个或多个自变量之间的线性关系模型。模型形式为：

Matlab实现

% 样本数据
X = [1; 2; 3; 4; 5];
Y = [2; 3; 5; 6; 8];

% 线性回归模型
X_ = [ones(size(X)), X]; % 增加常数项
beta = (X_' * X_) \ (X_' * Y);

% 预测
Y_pred = X_ * beta;

% 绘图
scatter(X, Y, 'bo');
hold on;
plot(X, Y_pred, 'r-');
xlabel('X');
ylabel('Y');
title('线性回归示例');
legend('数据点', '回归线');

1.2 多元回归

基本概念

多元回归用于研究因变量与多个自变量之间的关系。模型形式为：

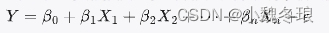
Matlab实现

% 样本数据
X1 = [1; 2; 3; 4; 5];
X2 = [2; 3; 4; 5; 6];
Y = [2; 3; 5; 6; 8];

% 多元线性回归模型
X_ = [ones(size(X1)), X1, X2];
beta = (X_' * X_) \ (X_' * Y);

% 预测
Y_pred = X_ * beta;

% 输出回归系数
disp(['回归系数：', num2str(beta')]);

1.3 非线性回归

基本概念

非线性回归用于拟合非线性关系的模型。常用的非线性模型包括指数模型、对数模型、幂模型等。

Matlab实现

% 样本数据
X = [1; 2; 3; 4; 5];
Y = [2; 4.1; 8.3; 16.2; 32.4];

% 非线性模型（幂模型）：Y = a * X^b
model_func = @(beta, X) beta(1) * X.^beta(2);
beta0 = [1, 1]; % 初始猜测

% 非线性回归
beta = nlinfit(X, Y, model_func, beta0);

% 预测
Y_pred = model_func(beta, X);

% 绘图
scatter(X, Y, 'bo');
hold on;
plot(X, Y_pred, 'r-');
xlabel('X');
ylabel('Y');
title('非线性回归示例');
legend('数据点', '拟合曲线');

2. 时间序列分析

2.1 时间序列的基本概念

时间序列是按照时间顺序排列的一组数据点，用于描述变量随时间的变化趋势。常见的时间序列分析方法包括移动平均、指数平滑和ARIMA模型。

2.2 移动平均

基本概念

移动平均用于平滑时间序列中的短期波动，识别长期趋势。

Matlab实现

% 样本时间序列数据
data = [22, 24, 25, 23, 26, 28, 27, 29, 30, 31];
window_size = 3; % 移动平均窗口大小

% 移动平均
moving_avg = movmean(data, window_size);

% 绘图
plot(data, 'b*-');
hold on;
plot(moving_avg, 'r-');
xlabel('时间');
ylabel('值');
title('移动平均示例');
legend('原始数据', '移动平均');

2.3 指数平滑

基本概念

指数平滑用于加强对时间序列中较新的数据点的关注，常见的包括单指数平滑、双指数平滑和三指数平滑。

Matlab实现

% 样本时间序列数据
data = [22, 24, 25, 23, 26, 28, 27, 29, 30, 31];
alpha = 0.2; % 平滑系数

% 单指数平滑
exp_smooth = zeros(size(data));
exp_smooth(1) = data(1); % 初始值
for t = 2:length(data)
    exp_smooth(t) = alpha * data(t) + (1 - alpha) * exp_smooth(t-1);
end

% 绘图
plot(data, 'b*-');
hold on;
plot(exp_smooth, 'r-');
xlabel('时间');
ylabel('值');
title('单指数平滑示例');
legend('原始数据', '单指数平滑');

2.4 ARIMA模型

基本概念

ARIMA模型用于捕捉时间序列中的自相关结构，是时间序列分析中最常用的方法之一。

Matlab实现

% 样本时间序列数据
data = [22, 24, 25, 23, 26, 28, 27, 29, 30, 31];

% 拟合ARIMA模型
model = arima('Constant', 0, 'D', 1, 'Seasonality', 0, 'MALags', 1, 'SMALags', 12);
fit = estimate(model, data');

% 预测
forecast_steps = 5;
[Y, YMSE] = forecast(fit, forecast_steps, 'Y0', data');

% 绘图
plot([data, Y']);
hold on;
plot(length(data)+1:length(data)+forecast_steps, Y, 'r*-');
xlabel('时间');
ylabel('值');
title('ARIMA模型示例');
legend('原始数据', '预测值');

3. 优化模型

3.1 线性规划

基本概念

线性规划用于求解目标函数在一组线性约束条件下的最大化或最小化问题。

Matlab实现

% 目标函数系数
f = [-1; -1];

% 约束矩阵和向量
A = [1, 2; 3, 1];
b = [6; 9];

% 下界和上界
lb = [0; 0];
ub = [inf; inf];

% 求解线性规划
[x, fval] = linprog(f, A, b, [], [], lb, ub);

% 输出结果
disp(['最优解：', num2str(x')]);
disp(['最优值：', num2str(-fval)]);

3.2 非线性规划

基本概念

非线性规划用于求解目标函数和/或约束条件为非线性的优化问题。

Matlab实现

% 目标函数
obj_fun = @(x) x(1)^2 + x(2)^2;

% 约束条件
nonlin_con = @(x) deal([], [x(1) + x(2) - 2]);

% 初始猜测
x0 = [0.5, 0.5];

% 求解非线性规划
options = optimoptions('fmincon', 'Display', 'iter');
[x, fval] = fmincon(obj_fun, x0, [], [], [], [], [], [], nonlin_con, options);

% 输出结果
disp(['最优解：', num2str(x)]);
disp(['最优值：', num2str(fval)]);

4. 微分方程模型

4.1 常微分方程模型

基本概念

常微分方程（ODE）用于描述变量随时间变化的动态过程，广泛应用于物理、化学、生物和经济等领域。常用的一阶和二阶微分方程可以分别表示为：

Matlab实现

% 设定初始条件和时间范围
y0 = 1; % 初始值
tspan = [0, 2]; % 时间区间

% 定义一阶微分方程
odefun = @(t, y) t * y;

% 求解微分方程
[t, y] = ode45(odefun, tspan, y0);

% 绘图
plot(t, y, 'b-');
xlabel('时间');
ylabel('y');
title('常微分方程示例');
legend('y(t)');

4.2 偏微分方程模型

基本概念

偏微分方程（PDE）用于描述具有多个独立变量的系统的动态行为，应用于热传导、流体力学、弹性力学等领域。典型的一维热传导方程表示为：

Matlab实现

% 定义空间和时间范围
x = linspace(0, 1, 20);
t = linspace(0, 1, 50);

% 定义初始条件
u0 = sin(pi * x);

% 设置PDE系数
m = 0;
alpha = 1;
pdefun = @(x,t,u,DuDx) alpha * DuDx;
icfun = @(x) sin(pi * x);
bcfun = @(xl,ul,xr,ur,t) [ul; ur];

% 求解PDE
sol = pdepe(m, pdefun, icfun, bcfun, x, t);

% 绘图
surf(x, t, sol);
xlabel('位置 x');
ylabel('时间 t');
zlabel('温度 u');
title('一维热传导方程的数值解');

4.3 微分方程模型的应用案例

案例：传染病模型

问题描述：研究一种传染病在一个封闭社区中的传播情况。

构建SIR模型：
SIR模型是一个常用的传染病模型，包含三个变量：易感者（Susceptible），感染者（Infected）和康复者（Recovered）。模型的微分方程为：

Matlab实现：

% 参数设置
beta = 0.3; % 感染率
gamma = 0.1; % 康复率
N = 1000; % 总人口
I0 = 1; % 初始感染者
R0 = 0; % 初始康复者
S0 = N - I0 - R0; % 初始易感者
y0 = [S0, I0, R0]; % 初始条件

% 定义SIR模型的微分方程
sir_ode = @(t, y) [-beta * y(1) * y(2) / N;
                   beta * y(1) * y(2) / N - gamma * y(2);
                   gamma * y(2)];

% 时间范围
tspan = [0, 160];

% 求解微分方程
[t, y] = ode45(sir_ode, tspan, y0);

% 绘图
plot(t, y(:, 1), 'b-', t, y(:, 2), 'r-', t, y(:, 3), 'g-');
xlabel('时间 (天)');
ylabel('人数');
title('SIR模型传染病传播模拟');
legend('易感者', '感染者', '康复者');

通过该案例，我们展示了SIR模型的构建和求解方法，读者可以根据实际情况调整参数，进一步探讨传染病传播的动态行为。

结语

在本篇文章中，我们详细介绍了几种典型的数学建模方法，包括回归分析、时间序列分析、优化模型和微分方程模型。通过具体的例子和Matlab代码示例，读者可以更好地理解这些方法的实际应用和实现过程。希望通过这些基础知识，读者能够在实际问题中灵活运用这些建模方法，解决复杂的系统问题。