目录
卷积码的基本概念：
卷积码与分组码的不同特点：
卷积码的构造与表示方法：
卷积码编码器的结构：
卷积码(3,1,3):
卷积码的卷积关系:
卷积码的生成矩阵:
卷积码的多项式:
系统码结构的卷积码:
卷积码的监督矩阵:
卷积码的监督多项式矩阵:
卷积码的状态图、树图与网格图描述:
卷积码的状态图:
卷积码的树图：
卷积码的网格图(篱笆图)：
卷积码的距离特性和转移函数:
自由距离:
卷积码的概率译码原理:
卷积码的维特比译码:
维特比译码的计算步骤：
卷积码的基本概念：
卷积码与分组码的不同特点：
卷积码的构造与表示方法：
卷积码编码器的结构：
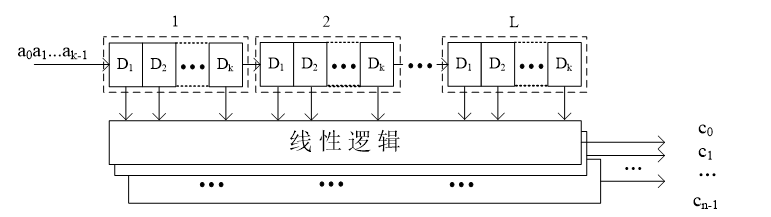
每输入 k 比特信息码组，输出一个 n 比特的码字
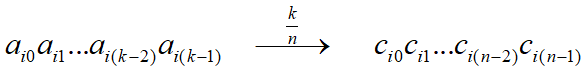
若每个输入信息码组，会影响L个编码输出的码字，则称该卷积码的约束长度为L，相应地，该卷积码记为（n,k,L）
卷积码编码效率：
卷积码(3,1,3):
每输入一个k=1 的信息码组，产生一个n=3的输出码字/码组
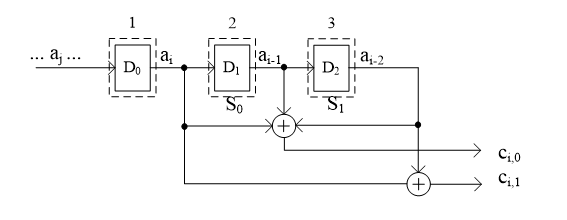
编码器结构
编码器输入与输出间的关系
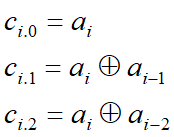
卷积码寄存器中保存的输入码组，称为编码器当前的状态。
卷积码(3,1,3)编码效率：
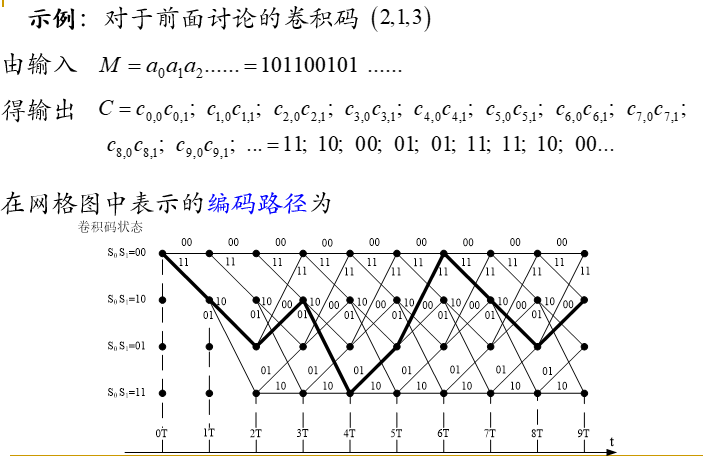
卷积码编码过程的示例:
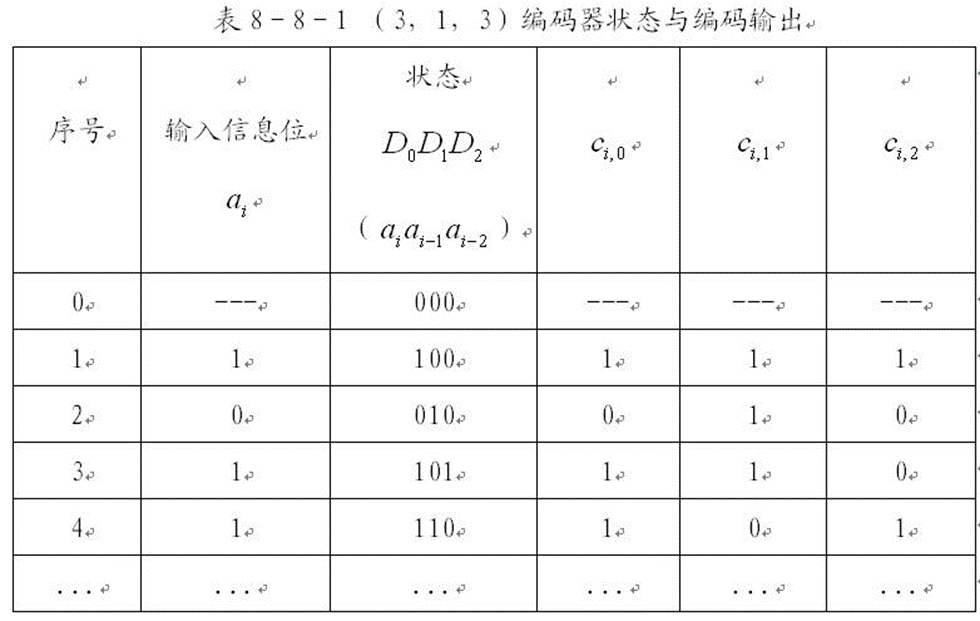
输入, 输出
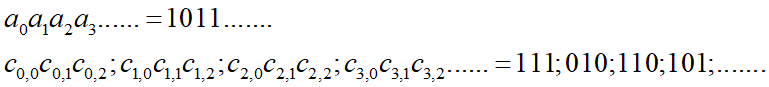
卷积码的卷积关系:
卷积码编码器的输入与输出间的关系是一种线性关系。
编码器的每一位输出，可视为一模2运算的线性滤波器的输出。
由相应的滤波器的单位脉冲响应，可将卷积码组中每一位的输出与输入的关系，用卷积运算来表示。
以上面的(3,1,3)卷积码为示例进行分析
设输入为一单位脉冲序列
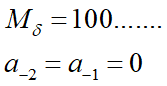
若
表示相应的第 i 个输出码组的第 j 位响应。
卷积码第0位到第3位的单位脉冲响应
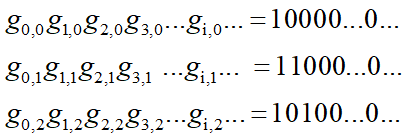
卷积码的生成矩阵:
单位脉冲响应可表示为
一般地，任意的一组输入信息码组总是可以表示为单位脉冲的组合。如输入序列
可分解为
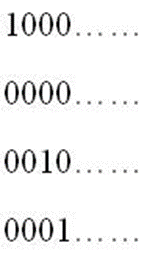
相应上述每个输入序列的编码输出按位累加得到最后的实际输出
若已知单位脉冲响应可表示为
卷积码的多项式:
卷积码的单位脉冲响应与多项式间可建立相应的关系。
如对前面讨论的卷积码，可定义每一位编码输出的生成多项式
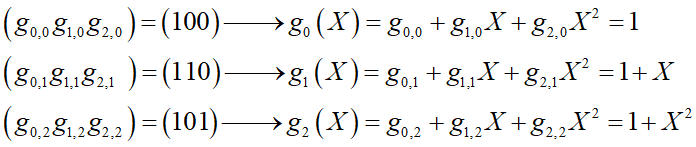
由此可定义多项式生成矩阵
若输入的信息序列用多项式表示为
则
其中
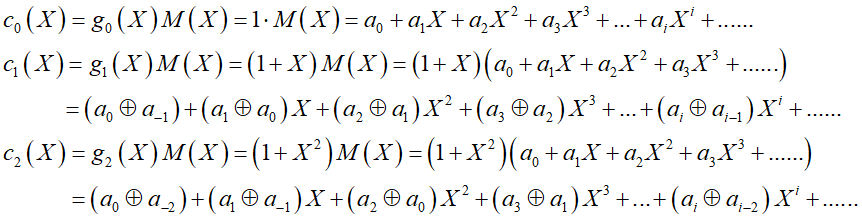
显然有
利用生成多项式计算的结果与前面的分析结果相同。
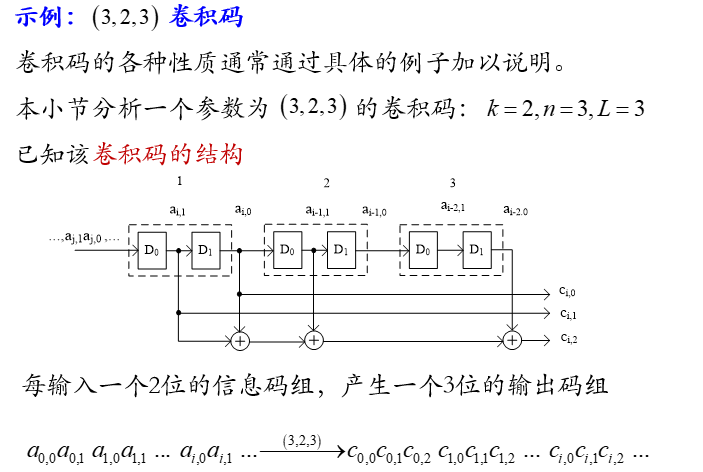
系统码结构的卷积码:
所谓系统码结构的卷积码与系统码结构分组码类似编码输出具有如下的结构
系统码结构的卷积码生成矩阵的一般形式
系统码结构的卷积码生成矩阵的一般形式
卷积码的监督矩阵:
卷积码的监督矩阵具有如下的形式
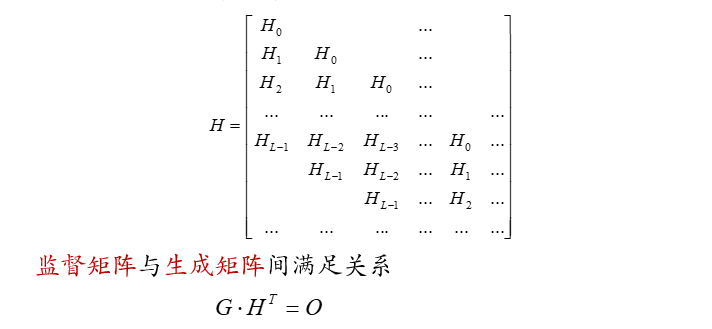
其中O是各个元素均为0的矩阵。从理论上来说，已知其中一个矩阵根据上述关系式可求另外矩阵。
已知系统码卷积码的生成矩阵为:
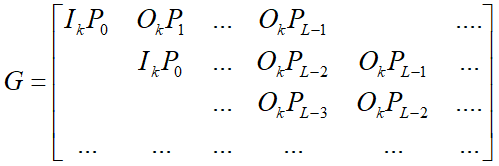
由此可得监督矩阵为
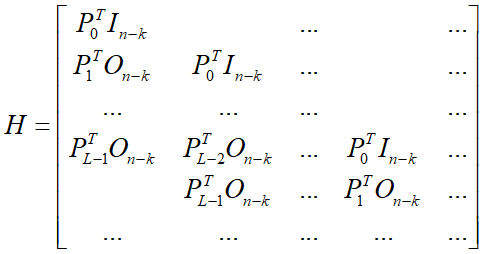
已知前述的
卷积码的生成矩阵为
其中与标准的生成多项式矩阵间的关系
由此可得监督矩阵
卷积码的监督多项式矩阵:
卷积码的监督多项式矩阵具有形式
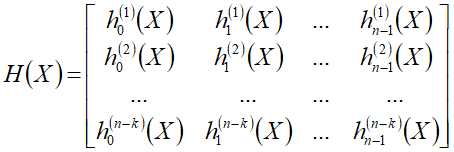
监督多项式矩阵与生成多项式矩阵应满足如下的关系
卷积码的状态图、树图与网格图描述:
卷积码是一种有记忆的编码，其记忆特性可通过状态图描述。
卷积码最重要的特点之一是可以通过维特比译码方式获得差错概率最小意义上的最佳的译码效果。
维特比译码与卷积码的状态图和网格图有密切的关系。
卷积码的状态图:
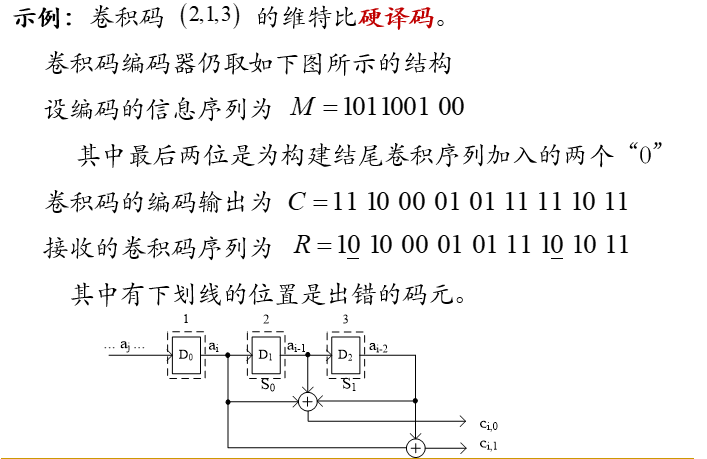
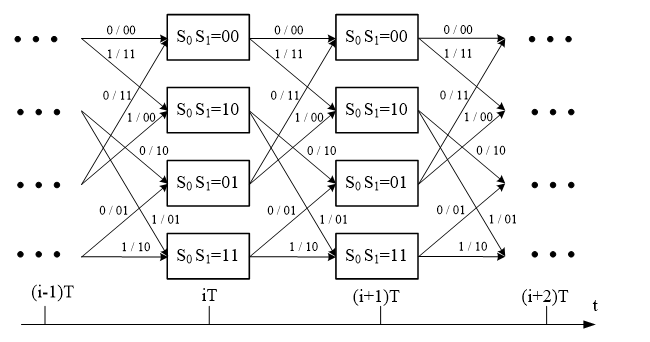
分析图示的参数为(2,1,3)的卷积码
编码的输出与输入及编码器当前的状态有关。
编码器的输出与当前的输入和编码器的状态间的关系
卷积码的树图：
卷积码的树图是另外一种表示编码器输出与输入及状态间关系的一种图形表示。
树图的特点：可直观看到随着输入和时序的变化，编器的输出和状态变化的整体情况
图例对应输入
输出
卷积码的网格图(篱笆图)：
状态图简单，但看不到随时序变化的编码过程
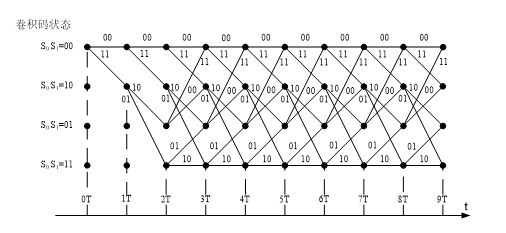
树图可看到随时序变化的编码过程，但图的大小随时间增加按指数增大。网格图是一种综合上述两种图形特点的一种编码描述方法。
由网格图图例可见，每增加一个编码的分组，网格图只会增加一节的长度，不会出现树图指数增大的情况。
对于卷积码
，每输入1位信息位，产生2位的编码输出。
当信息位为“0”时，总是沿着上分支转移到下一状态；
当信息位为“1”时，总是沿着下分支转移到下一状态；
在这种情况下，信息位在网格图中的标识可以省略。
从描述卷积码状态转换的特点来说，状态图、树图和网格图是等价的。
一般地，一个参数为（n,k,l）的卷积码
总共有
种不同的状态；每个状态有
个到达和离去的分支。
通常为避免编译码的复杂化，每个编码的信息分组的位数 k 和编码输出的分组长度 n 都取一个比较小的值。
卷积码的距离特性和转移函数:
自由距离:
卷积码的“距离”通常仍然是指卷积码间的汉明距离。卷积码的码组一般较短，通常将Lm个码组构成的一个序列作为一个编码的独立序列，亦可将这样的序列看作广义的“码字”。
是指卷积码“码字”间的最小汉明距离。卷积码仍然是一种线性码，最小码距与最小码重相等的关系依然成立。卷积码的自由距离，等于除了全零输出序列的路径之外的一条具有最小码重的路径。
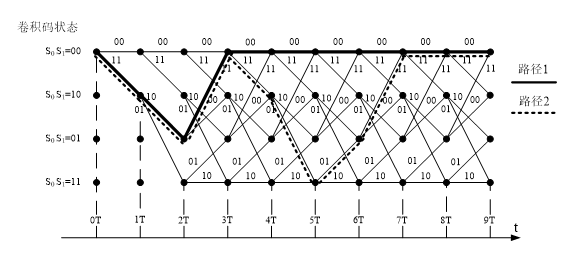
可以推测：码重最小的路径一定在离开全零状态，又回到全零路径后，沿着全零路径到编码结束的所有路径中，码重最小的路径。
卷积码的概率译码原理:
代数译码：主要利用码的代数结构；
概率译码：利用码的代数结构及信道的统计特性。主要方式包括序列译码，维特比译码
维特比译码是一种最大似然(差错最小意义上最佳)的译码方法。
最大似然译码:
卷积码的维特比译码:
卷积码的维特比译码是一种优化的最大似然的译码方法。
因为码字集中共有
种不同的码字，意味着要进行
求解似然函数的运算，运算量巨大。
简单的译码方法，接收完整个码字，与码字集中所有可能的码字进行比较，找出距离最小的码字作为输出。由上例可见计算复杂。维特比译码方法是一种有效减少运算量的算法。
维特比译码的思想：
理论上，网格图中共有
条不同的编码路径。
维特比译码过程接收码字中一个码组，进行一次比较，比较后，选择若干最可能获得正确译码结果的码段做后续比较。通过删除大量获得正确译码可能性小的码段，达到减少运算量的目的。
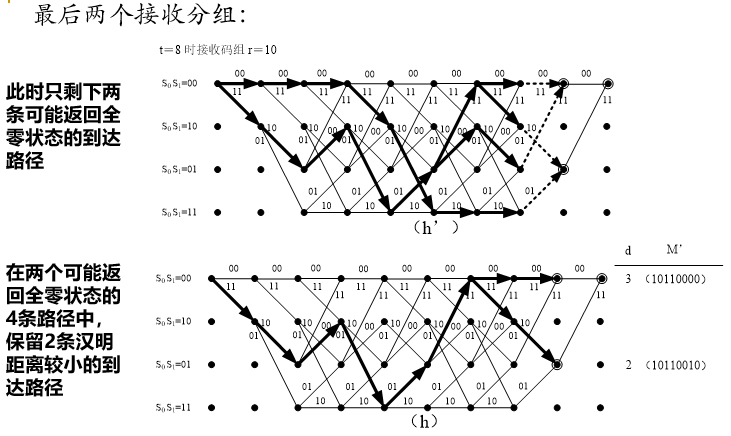
结尾卷积码序列：参数为
的卷积码，在编码完信息码组后，继续输入L-1个0字符，使编码路径返回全0状态的序列。
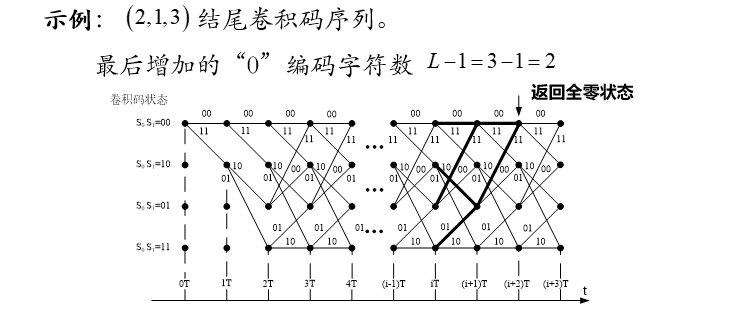
采用维特比译码的卷积码序列通常采用结尾卷积码序列的形式。
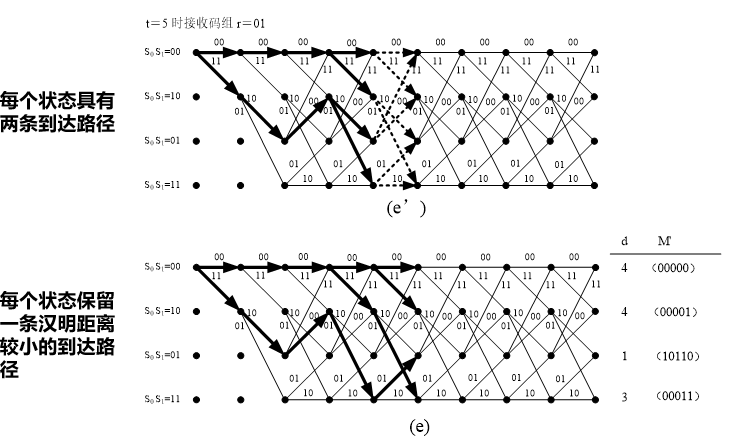
部分路径：在卷积码译码过程中在网格图中对应每个状态按照某种规则保留的一个行进路径称之。
路径度量值：在卷积码译码过程中确定网格图中选留路径的度量值。在维特比译码中，汉明或欧氏距离越小相应的度量值越大。
维特比译码过程中的距离：输入序列与网格图中部分路径所对应输出码字序列的汉明(对硬译码)或欧氏(对软译码)距离。
维特比译码的计算步骤：
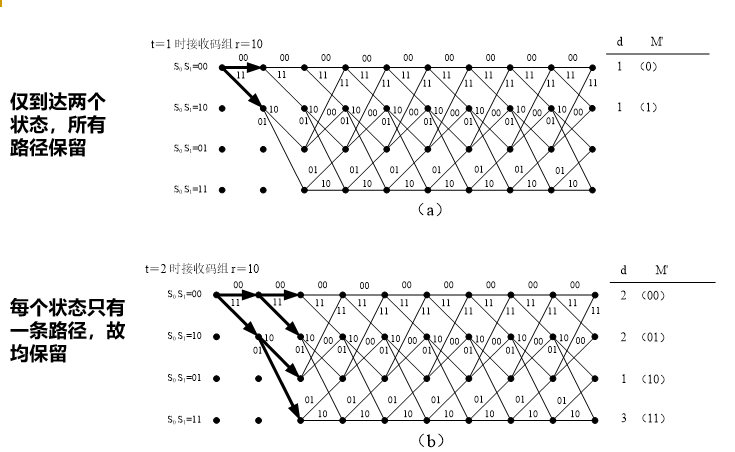
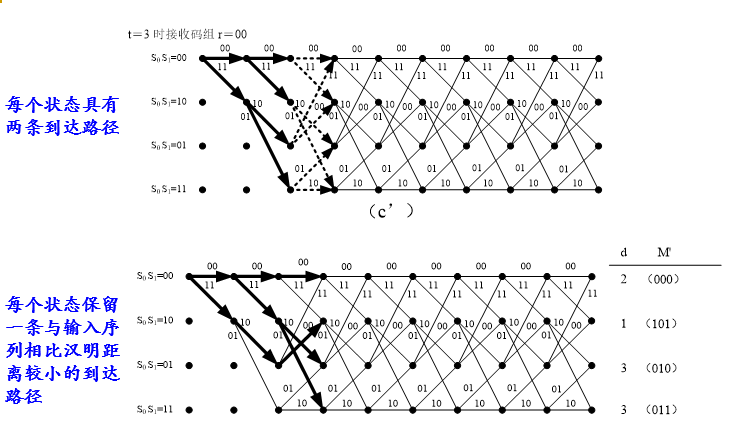
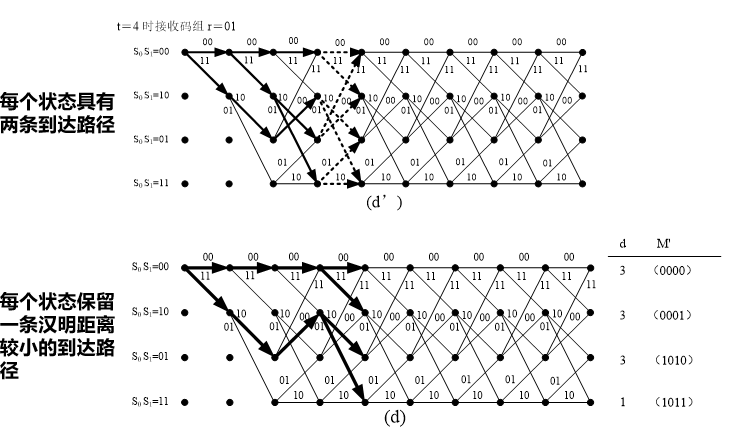
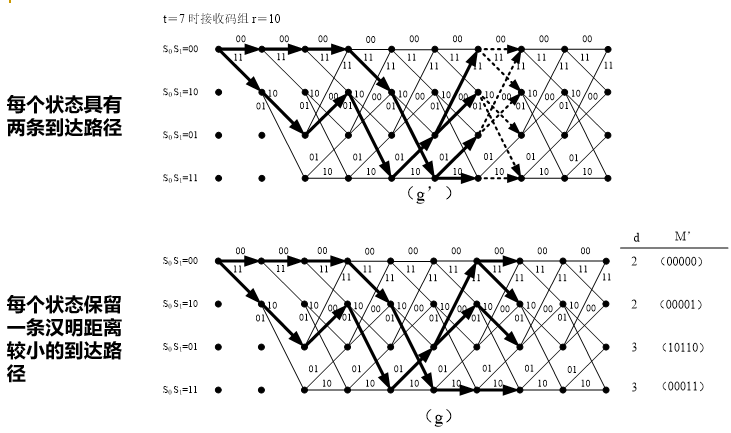
1) 输入一个 n 位的编码码组，计算码组输入后新到达每个状态的2k个可能选留路径的度量值，每个状态仅保留其中度量值最大的路径作为选留路径。如有相同值的路径，则任选其一。
度量值可根据选留路径与输入序列的相似程度来确定。
(2) 译码时间参数 t 加1
(3) 根据获得的最后一条选留路径，获得相应的译码输出码字。
