题目
题目链接🔗
如果一个字符串满足以下条件,则称其为 美丽字符串 :
- 它由英语小写字母表的前 k 个字母组成。
- 它不包含任何长度为 2 或更长的回文子字符串。
给你一个长度为 n 的美丽字符串 s 和一个正整数 k 。
请你找出并返回一个长度为 n 的美丽字符串,该字符串还满足:在字典序大于 s 的所有美丽字符串中字典序最小。如果不存在这样的字符串,则返回一个空字符串。
对于长度相同的两个字符串 a 和 b ,如果字符串 a 在与字符串 b 不同的第一个位置上的字符字典序更大,则字符串 a 的字典序大于字符串 b 。
- 例如,“abcd” 的字典序比 “abcc” 更大,因为在不同的第一个位置(第四个字符)上 d 的字典序大于 c 。
示例 1:
输入:s = “abcz”, k = 26
输出:“abda”
解释:字符串 “abda” 既是美丽字符串,又满足字典序大于 “abcz” 。
可以证明不存在字符串同时满足字典序大于 “abcz”、美丽字符串、字典序小于 “abda” 这三个条件。
示例 2:
输入:s = “dc”, k = 4
输出:“”
解释:可以证明,不存在既是美丽字符串,又字典序大于 “dc” 的字符串。
提示:
- 1 ≤ n = s . l e n g t h ≤ 1 0 5 1 \leq n = s.length \leq 10^5 1≤n=s.length≤105
- 4 < = k < = 26 4 <= k <= 26 4<=k<=26
-
s
是一个美丽字符串
s 是一个美丽字符串
s是一个美丽字符串
思路
首先,我们分析一下美丽字符串的条件:美丽字符串由前 k 个小写字母组成,并且不包含任何长度为 2 或更长的回文子字符串。为了满足这个条件,只需要确保每个字符都不与其前两个字符相同。
接下来,我们需要找到一个字典序大于给定字符串 s 的美丽字符串,并且在所有可能的字符串中字典序最小。为了实现这一点,可以采用贪心算法,从字符串末尾开始逐个字符递增,直到找到满足条件的字符位置。
具体步骤
- 寻找可以增大的字符位置:
- 从字符串末尾开始,逐个字符向前尝试将字符增大。
- 对于每个字符位置,尝试将其递增一个字符,同时确保新字符不与其前两个字符相同。
- 字符递增并检测美丽字符串条件:
- 找到一个可以增大的字符位置后,将其递增,同时保证新字符不引入长度为 2 或 3 的回文子字符串。
- 更新该字符后,需要将其后面的字符重置为最小可能值,以确保生成的字符串在字典序上最小。
- 处理未找到可增大字符位置的情况:
- 如果从头到尾都没有找到可以增大的字符位置,则返回空字符串,表示不存在符合条件的字符串。
- 如果从头到尾都没有找到可以增大的字符位置,则返回空字符串,表示不存在符合条件的字符串。
代码
class Solution {
public:
string smallestBeautifulString(string s, int k) {
int n = s.size();
int index = n - 1;
// 步骤 1:寻找可以增大的字符位置
while (index >= 0) {
int t = s[index] + 1;
// 跳过会导致回文子串的字符
while (t < 'a' + k && (index > 0 && t == s[index - 1] || index > 1 && t == s[index - 2])) {
++t;
}
if (t < 'a' + k) {
s[index] = t;
break;
}
--index;
}
// 如果没有找到可增大的字符位置,返回空字符串
if (index < 0) return "";
// 步骤 2:调整剩余的字符为最小的合法字符
for (int i = index + 1; i < n; ++i) {
s[i] = 'a';
// 跳过会导致回文子串的字符
while (s[i] == s[i - 1] || (i > 1 && s[i] == s[i - 2])) {
++s[i];
}
}
return s;
}
};
复杂度分析
时间复杂度
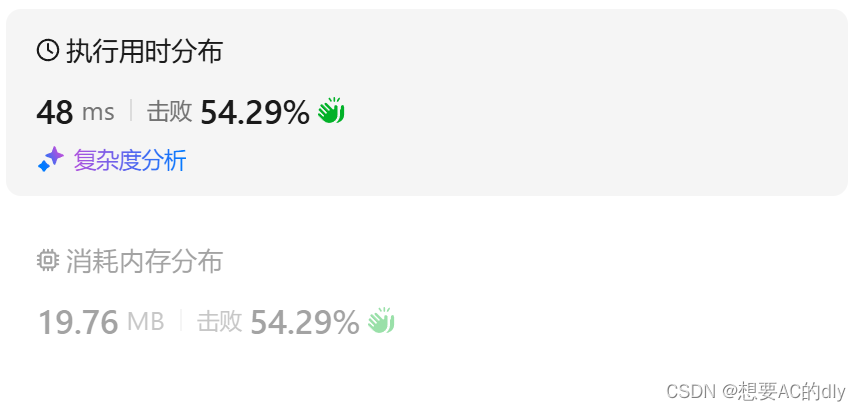
- 时间复杂度:O(n),因为我们最多需要遍历字符串两次。
空间复杂度
- 空间复杂度:O(1),只使用了常数级别的额外空间。
结果
总结
通过上述方法,我们能有效地找到满足条件的下一个美丽字符串。这种方法不仅保证了生成字符串的字典序大于给定字符串,还确保了字典序最小。该解决方案结合了贪心算法和条件检查,使其在处理大规模输入时依然高效可靠。