1. 优先级队列
队列是一种先进先出(FIFO)的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列,该场景下,使用队列不合适
在这种情况下,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象,这种数据结构就是优先级队列(Priority Queue)
2. 优先级队列的模拟实现
2.1 堆的概念
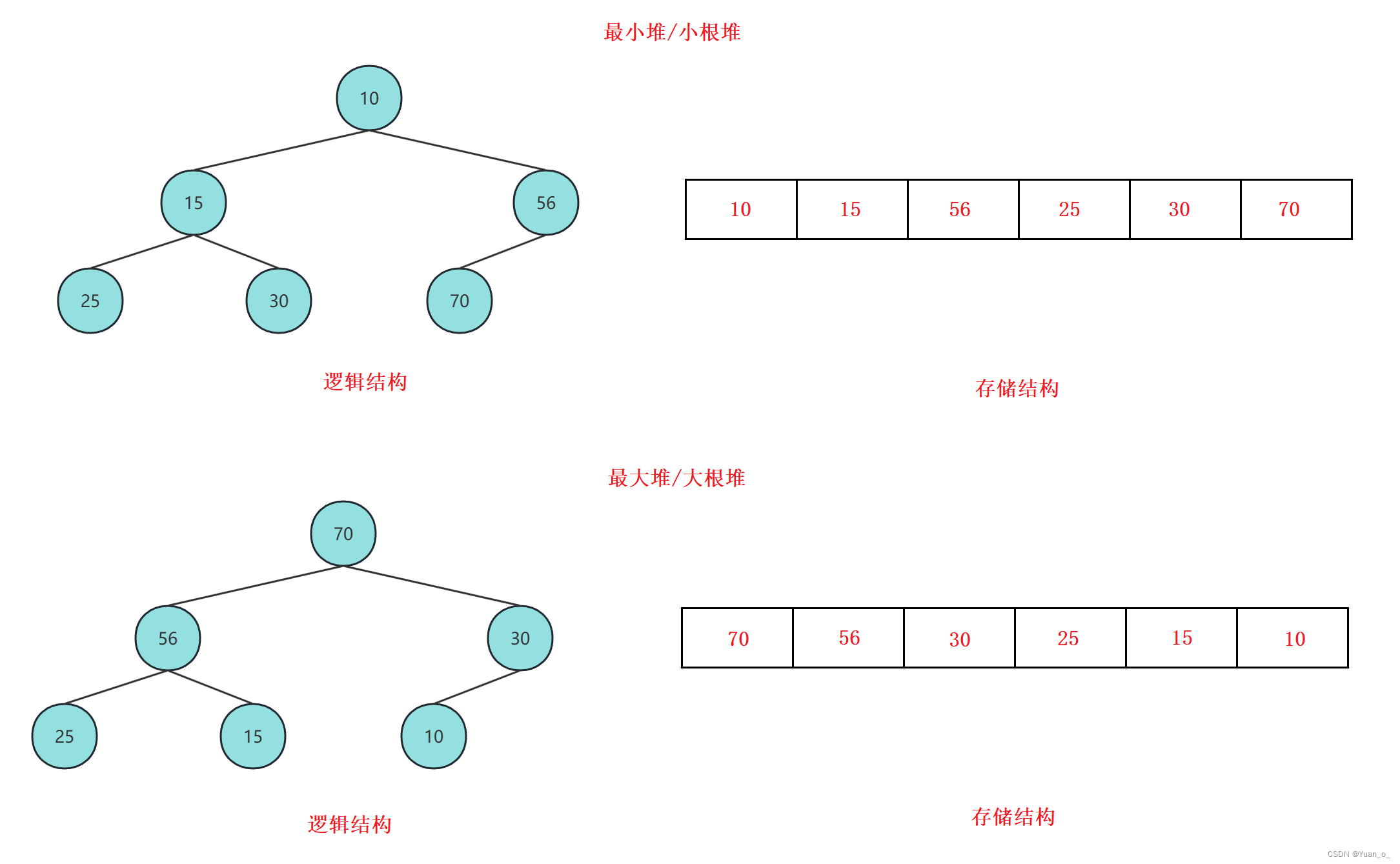
性质:
如上图,堆中某个节点的值总是不大于其父节点的值,称为最小堆/小根堆
堆中某个节点的值总是不小于其父节点的值,称为最大堆/大根堆
堆总是一棵完全二叉树
2.2 堆的存储方式
从堆的概念可知,堆是一棵完全二叉树,因此可用层序的规则采用顺序的方式进行高效存储
tip:对于非完全二叉树则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率较低
将元素存储到数组中后,假设 i 为节点在数组中的下标,则有:
- 如果 i 为0,则 i 表示的节点为根节点,否则 i 节点的双亲结点为(i - 1)/2
- 如果 2*i+1 小于节点个数,则节点 i 的左孩子下标为 2*i+1 ,否则没有左孩子
- 如果 2*i+2 小于节点个数,则节点 i 的右孩子下标为 2*i+2 ,否则没有右孩子
2.3 堆的创建
2.3.1 堆向下调整
以集合{ 27,15,19,18,28,34,65,49,25,37 }为例,转换为大根堆的过程:
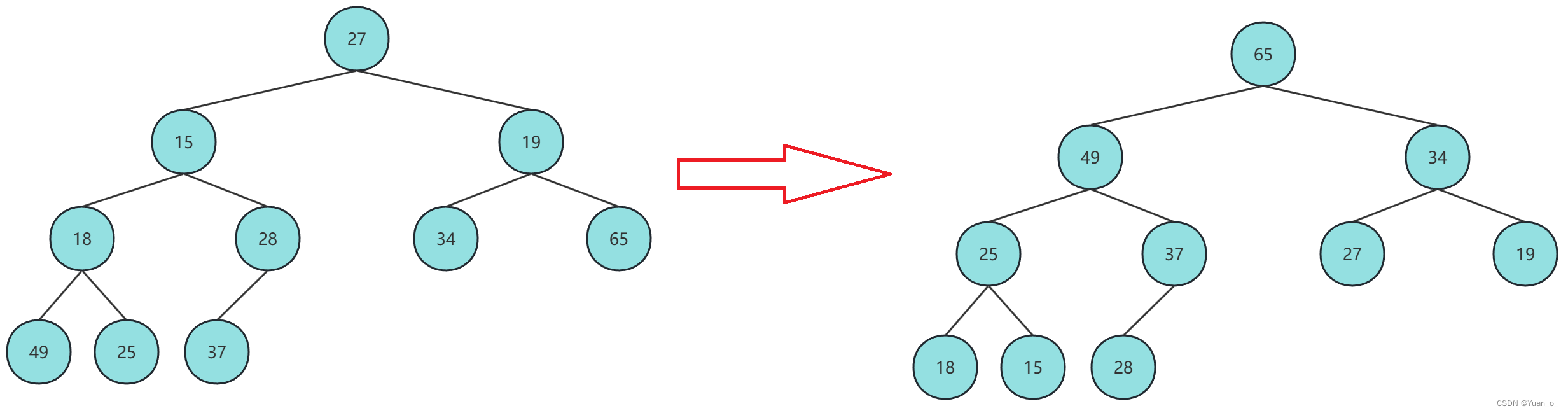
//TestHeap 类
public class TestHeap {
public int[] elem;//堆由数组实现
public int usedSize;//记录有效数据个数
public TestHeap() {//构造方法
this.elem = new int[10];
}
public void init(int[] array) {//给数组初始化
for (int i = 0; i < array.length; i++) {
elem[i] = array[i];
usedSize++;
}
}
//把elem数组中的数据调整为大根堆
public void createHeap() {
//让parent初始位置在树的最后一棵子树的根节点处,用到公式:根节点 = (i-1)/2
//其中usedSize-1表示最后一个节点,从上到下循环遍历整棵树
for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {
//siftDown方法用来判断树中左右孩子与父亲节点的大小关系
siftDown(parent,usedSize);
}
}
//交换函数
public void swap(int i, int j) {
int tmp = elem[i];
elem[i] = elem[j];
elem[j] = tmp;
}
public void siftDown(int parent, int end) {
int child = 2*parent+1;//公式:左孩子下标 = 2*根节点下标+1
while(child < end) {//end是有效数据个数,不能用<=
//下面if走完之后,child一定是左右孩子中最大值的下标
if(child+1 < end && elem[child] < elem[child+1]) {
child++;
}
//下面if判断孩子节点是否大于父亲节点,若大于则交换,否则跳出循环,去判断上一棵树
if(elem[child] > parent) {
swap(child,parent);
parent = child;
child = 2*parent+1;
}else {
break;
}
}
}
}
//Test 类
public class Test {
public static void main(String[] args) {
int[] array = {27,15,19,18,28,34,65,49,25,37};
TestHeap testHeap = new TestHeap();
testHeap.init(array);
testHeap.createHeap();
}
}
tip:在调整以parent为根的二叉树时,必须要满足parent的左子树和右子树已经是堆,才可以向下调整
时间复杂度:最坏的情况就如上例,从根一路比较到叶子,比较的次数为完全二叉树的高度,即时间复杂度为
2.3.2 建堆的时间复杂度
推导:
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了方便计算,使用满二叉树来推导
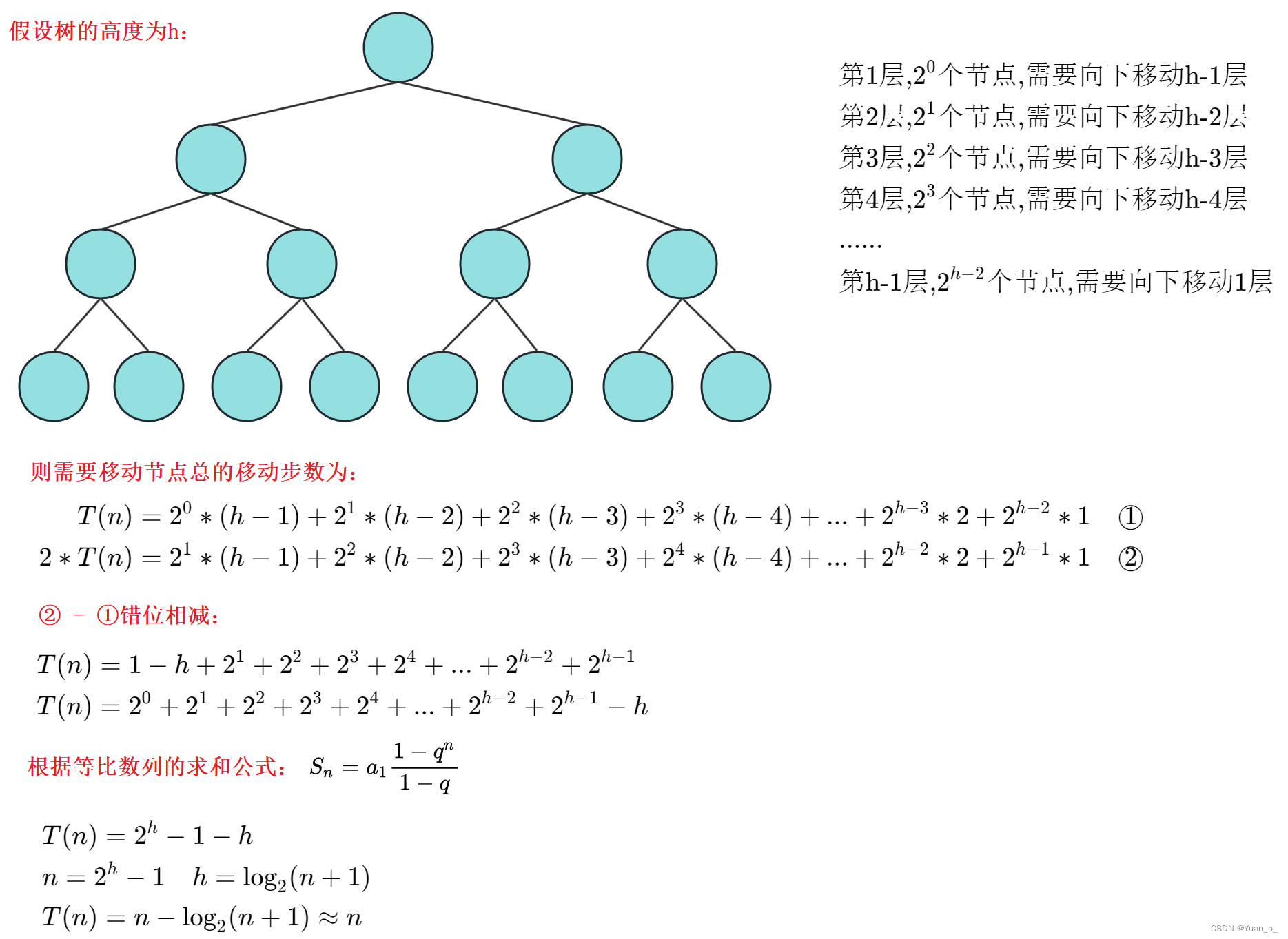
结论: 建堆的时间复杂度为 O(N)
2.4 堆的插入与删除
2.4.1 堆的插入
堆的插入需要两步
1. 先将元素放到树底层最后一个节点(空间不够时扩容)
2. 将插入新节点向上调整,直到满足堆的性质

public void offer(int val) {
if(isFull()) {//判满,若满则扩容
elem = Arrays.copyOf(elem,2*elem.length);
}
elem[usedSize] = val;//val赋值到usedSize位置,usedSize++
usedSize++;
siftUp(usedSize-1);//向上调整
}
public void siftUp(int child) {
int parent = (child-1)/2;//通过孩子节点找到父亲节点
while(parent >= 0) {//当父亲节点下标小于0,说明向上调整结束了,堆已有序
if(elem[child] > elem[parent]) {//孩子节点的值大于父亲节点值,即交换
swap(child,parent);
child = parent;
parent = (child-1)/2;
}else {//若孩子节点的值小于父亲节点的值,说明堆已有序,直接跳出循环
break;
}
}
}
public boolean isFull() {
return usedSize == elem.length;
}2.4.2 堆的删除
tip:堆的删除一定删除的是堆顶元素,分为三步:
1. 将堆定元素对堆中最后一个元素交换
2. 将堆中有效数据个数减少一个
3. 对堆顶元素进行向下调整
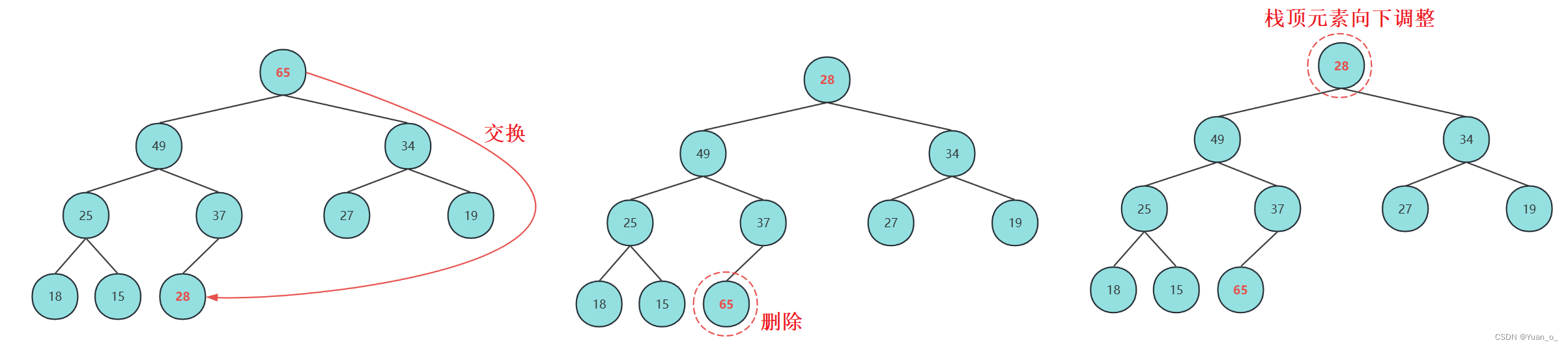
public int poll() {
if(isEmpty()) {//若栈空,返回-1
return -1;
}
int old = elem[0];//记录要删除的数据,最后返回
swap(0,usedSize-1);//交换堆顶元素和最后元素
usedSize--;//有效个数--
siftDown(0,usedSize);//从堆定开始,向下调整
return old;
}
public boolean isEmpty() {
return usedSize == 0;
}例题:
1.下列关键字序列为堆的是:()
A: 100,60,70,50,32,65 B: 60,70,65,50,32,100 C: 65,100,70,32,50,60
D: 70,65,100,32,50,60 E: 32,50,100,70,65,60 F: 50,100,70,65,60,32
选A
2.已知小根堆为8,15,10,21,34,16,12,删除关键字8之后需重建堆,在此过程中,关键字之间的比较次数是()
A: 1 B: 2 C: 3 D: 4
解析:选C,15与10比,12与10比,12与16比
3.最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后,其结果是()
A: [3,2,5,7,4,6,8] B: [2,3,5,7,4,6,8]
C: [2,3,4,5,7,8,6] D: [2,3,4,5,6,7,8]
选C
3. 常用接口介绍
3.1 PriorityQueue的特性
Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的,本文主要介绍PriorityQueue
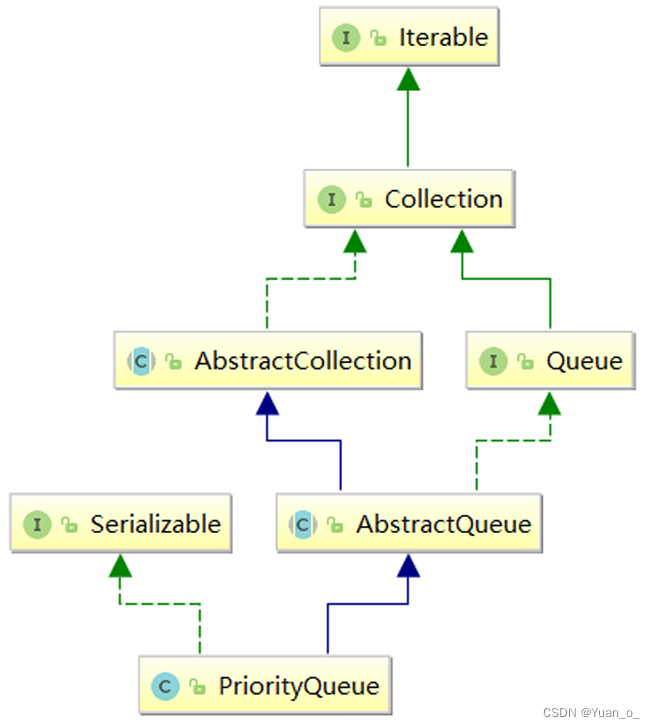
public static void main(String[] args) {
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
priorityQueue.offer(1);
priorityQueue.offer(2);
priorityQueue.offer(3);
System.out.println(priorityQueue.poll());//运行结果:1
System.out.println(priorityQueue.poll());// 2
}关于PriorityQueue的使用注意:
- 1.使用时必须导入PriorityQueue所在的包,即:import java.util.PriorityQueue;
- 2. PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出 ClassCastException 异常
- 3. 不能插入null对象,否则会抛出 NullPointerException
- 4. 没有容量限制,可以插入任意多个元素,其内部可以自动扩容
- 5. 插入和删除元素的时间复杂度为
- 6. PriorityQueue底层使用了堆数据结构
- 7. PriorityQueue默认情况下是小堆---即每次获取到的元素都是最小的元素
3.2 PriorityQueue常用接口介绍
3.2.1 优先级队列的构造
此处只是常见的几种:
| 构造器 | 功能介绍 |
| PriorityQueue() | 创建一个空的优先级队列,默认容量是11 |
| PriorityQueue(int initialCapacity) | 创建一个初始容量为initialCapacity的优先级队列,注意: initialCapacity不能小于1,否则会抛IllegalArgumentException异 常 |
| PriorityQueue(Collection c) | 用一个集合来创建优先级队列 |
构造方法原理:

用一个集合来创建优先级队列:
class Student {
}
public class Test {
public static void main(String[] args) {
ArrayList<Integer> arrayList = new ArrayList<>();
arrayList.add(1);
arrayList.add(2);
arrayList.add(3);
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(arrayList);
priorityQueue.offer(4);
priorityQueue.offer(5);
priorityQueue.offer(6);
System.out.println(priorityQueue.poll());//运行结果:1
System.out.println(priorityQueue.poll());// 2
PriorityQueue<Student> priorityQueue1 = new PriorityQueue<>(arrayList);//error
//传入参数必须是Student类或其子类
}
}3.2.2 offer元素原理:
查看源码:
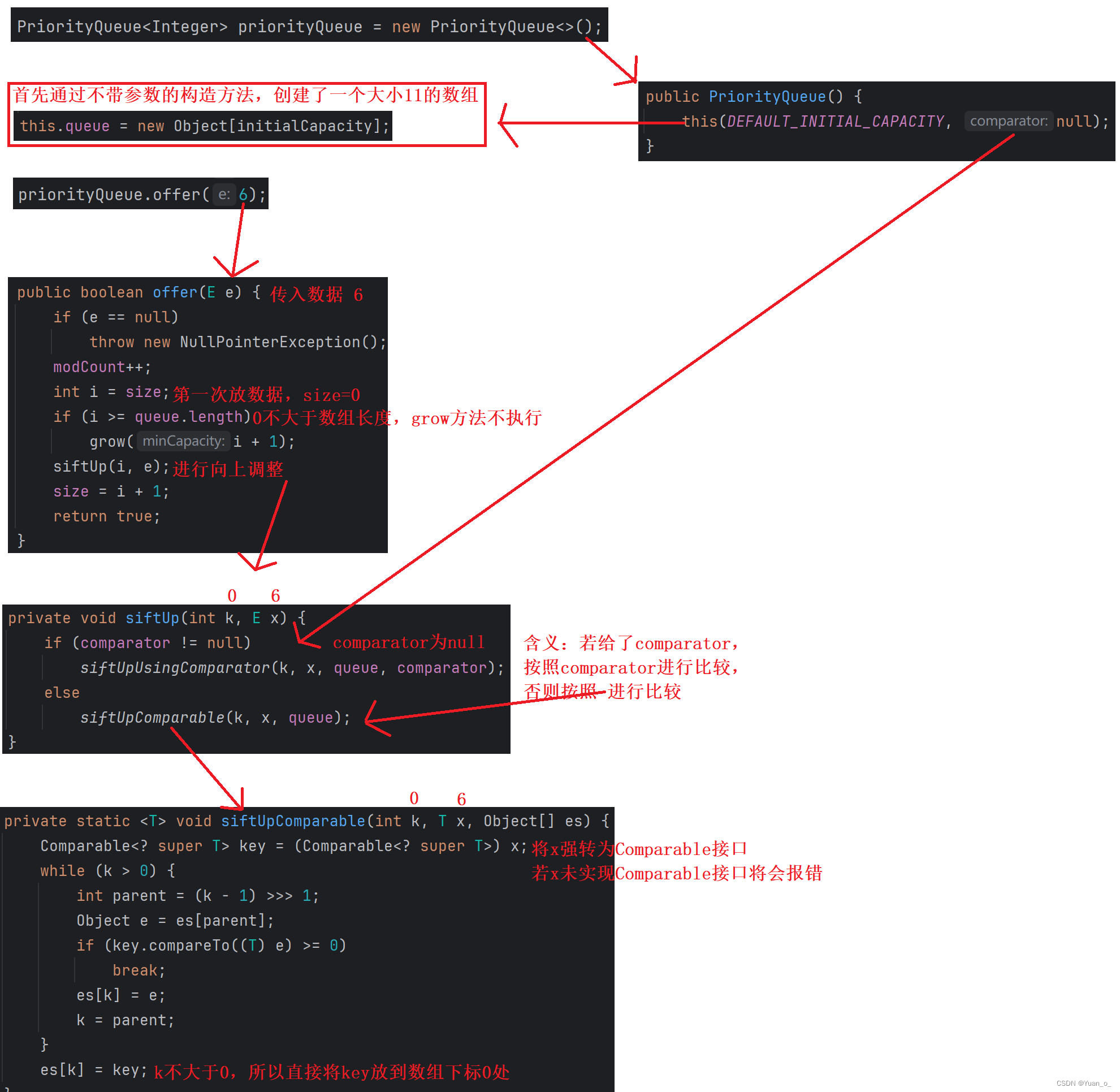
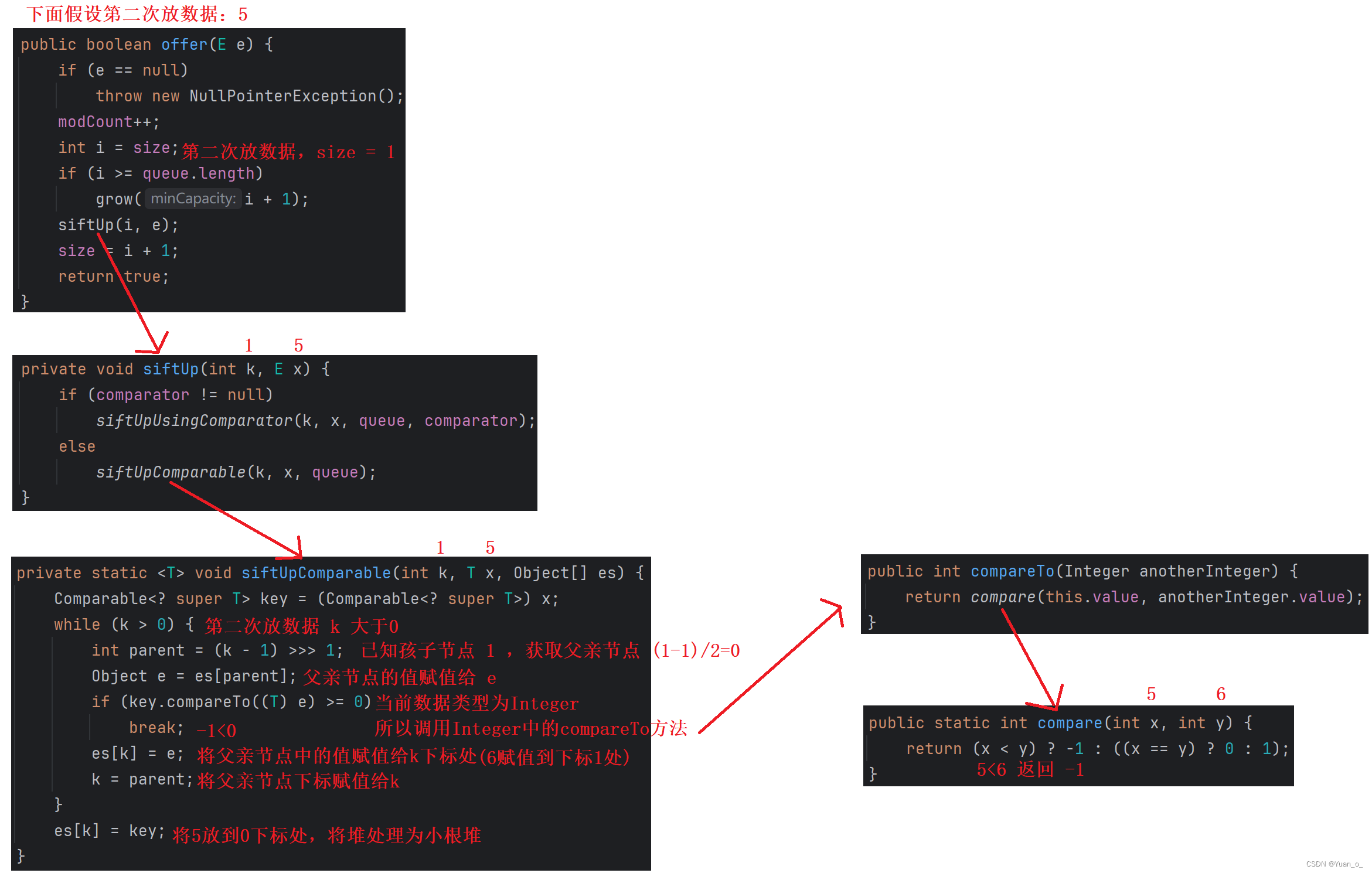
结合上面创建小根堆的流程分析:
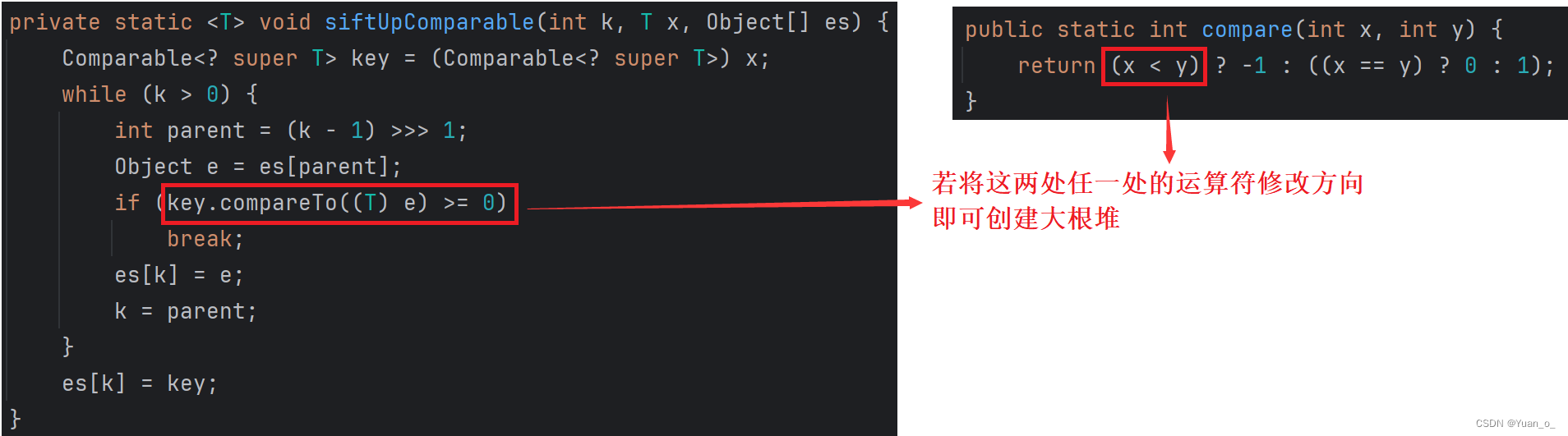
自己实现比较器:
//实现小根堆的比较器
class IntCmp implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o1.compareTo(o2);//小根堆
}
}
public class Test {
public static void main(String[] args) {
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new IntCmp());//别忘了此处new比较器对象作为参数
priorityQueue.offer(4);
priorityQueue.offer(5);
priorityQueue.offer(6);
System.out.println(priorityQueue.poll());//运行结果:4
System.out.println(priorityQueue.poll());// 5
}
}
//实现大根堆的比较器
class IntCmp implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);//大根堆 两比较器仅有此处不同!!!!!!!!!!!!!!
}
}
public class Test {
public static void main(String[] args) {
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new IntCmp());
priorityQueue.offer(4);
priorityQueue.offer(5);
priorityQueue.offer(6);
System.out.println(priorityQueue.poll());//运行结果:6
System.out.println(priorityQueue.poll());// 5
}3.2.3 PriorityQueue的扩容方式
以下是JDK17中的源码:
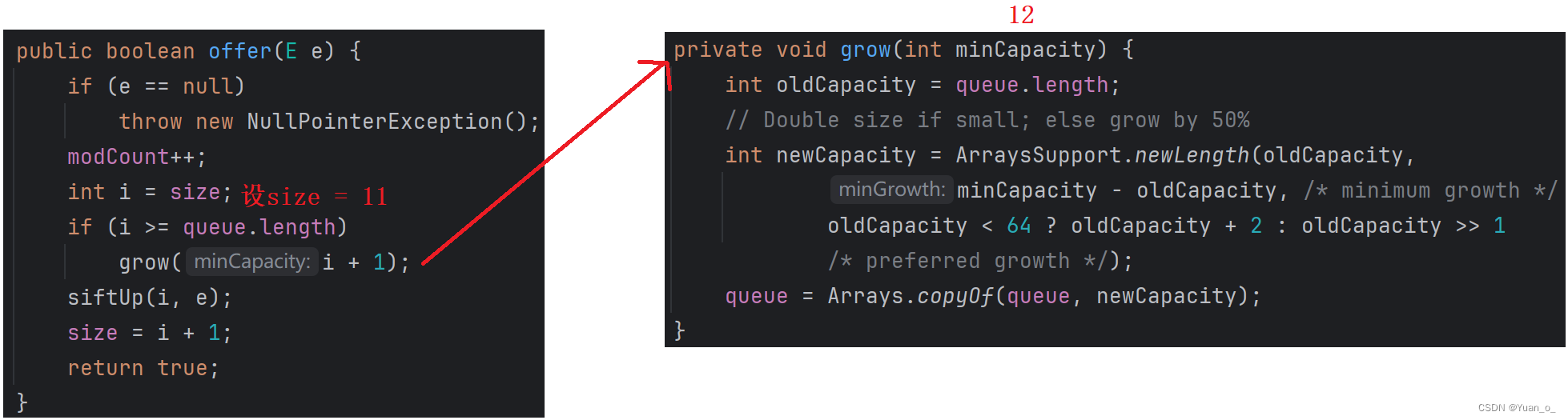
说明:
如果容量小于64时,按照oldCapacity的2倍方式扩容
如果容量大于等于64,按照oldCapacity的1.5倍方式扩容
如果容量超过MAX_ARRAY_SIZE,按照MAX_ARRAY_SIZE来进行扩容
3.3 OJ练习
top-k问题:最大或最小的前k个数据
public static int[] smallestK(int[] arr, int k) {
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
for (int i = 0; i < arr.length; i++) {
minHeap.offer(arr[i]);
}
int[] tmp = new int[k];
for (int i = 0; i < k; i++) {
int val = minHeap.poll();
tmp[i] = val;
}
return tmp;
}
public static void main(String[] args) {
int[] array = {27,15,19,18,28};
int[] ret = smallestK(array,3);
System.out.println(Arrays.toString(ret));
}运行结果:
虽然上述方法也能满足需求,但是其时间复杂度为
不是非常好的解决方案,现需要一个时间复杂度更小的方法:
若求前K个最小的数字
1. 先把前 K 个元素建立大小为K的大根堆
2. 遍历剩余 N-K 个元素,若堆顶元素大于当前 i 下标的值就出堆
这样遍历完数组后,大小为 K 的堆中就是最小的 K 个元素
反之求前K个最大的数字就建立小根堆
class IntCmp implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);//大根堆
}
}
class Solution {
public int[] smallestK(int[] arr, int k) {
int[] tmp = new int[k];
if(k == 0) {
return tmp;
}
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new IntCmp());
//1.把前K个元素放进堆中
for (int i = 0; i < k; i++) {
maxHeap.offer(arr[i]);
}
//2.遍历剩下的 N-k 个元素
for (int i = k; i < arr.length; i++) {
int val = maxHeap.peek();
if(val > arr[i]) {
maxHeap.poll();
maxHeap.offer(arr[i]);
}
}
//3.将堆中元素放到数组中
for (int i = 0; i < k; i++) {
tmp[i] = maxHeap.poll();
}
return tmp;
}
}变种题:求第K小的数据,建立大根堆,堆顶元素就是第K小
3.4 堆排序
要求:在原堆上修改,不能新建
方法两步:
1. 建堆:
- 要求升序,建大堆
- 要求降序,建小堆
2. 利用堆删除来进行排序
建堆和堆删除中都用到了向下调整
//堆排序 升序
public void heapSort() {
int endIndex = usedSize-1;
while(endIndex > 0) {
swap(0,endIndex);
siftDown(0,endIndex);
endIndex--;
}
}