GNN Algorithms(8): DDPM

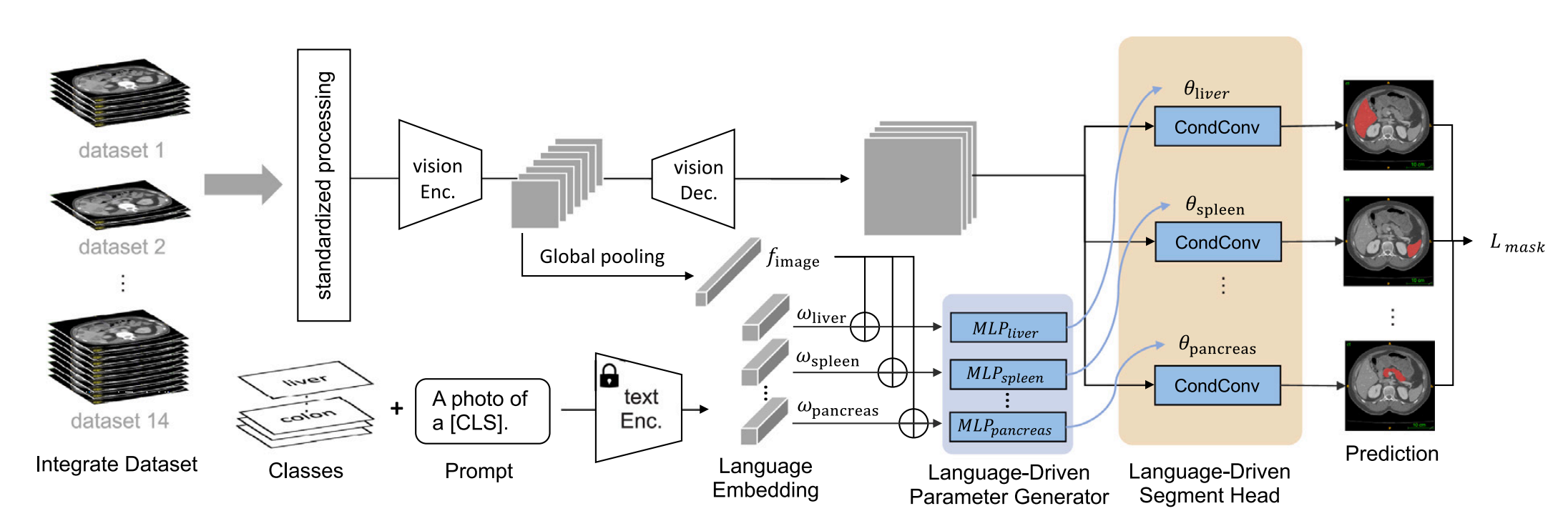
扩散模型 diffusion model：正向扩散过程 Forward Diffusion Process、反向生成过程 Reverse Generation Process.

本质：DDPM, Denoising Diffusion Probabilistic Model

T steps 加噪：没有参数， $q(x_t|x_{t-1})$ ->随机取一个每一步都要加的随机高斯噪声 $\epsilon$ value，T步后生成一个符合正态分布的纯噪声图像 $x_T$ ，这其实也是个噪声noise。
T steps 去噪：有参数， $p_{\theta}(x_t|x_{t-1})$ ->模型生成一个每一步需要剔除的模拟高斯噪声 $\epsilon_{\theta}$ ，从噪声图像noise中恢复出一个新的清晰、有意义的图像。
关键：构造一个优质的去噪模型去估计反向过程中的随机噪声 $\epsilon_{\theta}$ ，U-Net or ResNet。

1. Background

1.1 VAE

1.2 GAN

1.3 DDPM

2. Diffusion Model Pipeline 流程

2.1 前向扩散过程

2.2 反向生成过程

2.3 Diffusion model优缺点

3. DDPM Formulation Derivation

3.1 前向过程

3.2 反向过程

4. DDPM implementation on MNIST

参考

1. Background

一般来说，图像生成模型根据随机数生成图像，被用于解决训练数据不足的问题，但生成任务缺乏有效的指导 label，那如何让神经网络生成的图像向[标准答案] or [理想答案]靠拢？

为了解决这一问题，人们设计了专门用于生成图像的NN model：VAE, GAN, DDPM。

1.1 VAE

VAE，Variational Auto-Encoder，变分自编码器，在2013年提出于paper Auto-Encoding Variational Bayes，通过学习数据的概率分布来生成新样本。因为直接学习向量生成的图像很困难，也没有label指导，所以VAE先把图像变成向量，再用该向量生成图像。

VAE模型 architecture：编码器、概率潜在空间、解码器。在training stage，encoder预测每个图像的均值和方差，然后从高斯分布中对这些值进行采样，并将其传递到decoder中，其中输入图像预计与输出图像相似。这个过程包括KL Divergence计算loss。

VAE 优点：能够生成各种各样的图像。

缺点：可能就是准确度差点意思。

reference：https://adaning.github.io/posts/9047.html

1.2 GAN

GAN, Generative Adversarial Networks，生成式对抗网络，提出于 NeurlPS 2014 paper: Generative Adversarial Nets。通过训练两个神经网络(生成器和判别器)互相对抗来学习数据分布。

- generator，生成器接受一个随机噪声noise作为输入，输出一个图片向量。

- discriminator，接受一个真实图像作为输入，生成真实图像向量。

- 对抗损失loss，Jensen-Shannon散度，Wasserstein距离，最小二乘损失，铰链损失Hinge Loss。

GAN优点：GANs擅长生成与训练集图像非常相似的图像。

缺点：GANs生成图像的目标追求与training图像高度一致，缺乏多样性。

reference：简单使用PyTorch搭建GAN模型 | 机器之心

1.3 DDPM

DDPM = VAE + GAN，生成高精度且多样性强的伪图像。

DDPM，在2020年提出于paper：Denoising Diffusion Probabilistic Models。

2. Diffusion Model Pipeline 流程

Diffusion model是一类生成模型，包括：前向扩散过程和反向生成过程。在正向过程中，原始真实图像输入x0会不断混入高斯噪声 $\epsilon$ ，经过T次加噪后，图像 $x_T$ 会变成一幅符合标准正态分布的纯噪声图像，即纯纯的noise；在反向生成过程中，我们希望训练出一个去噪神经网络 $\theta$ ，该网络能够预估反向过程中每一步需要剔除的模拟高斯噪声 $\epsilon_{\theta}$ ，T步去噪后把噪声图像noise $x_T$ 还原回x0。

2.1 前向扩散过程

在这个过程中，diffusion model通过逐步向图像数据添加高斯噪声，使其变得越来越模糊，最终使noise数据分布接近标准正态分布。
具体来说，给定一个初始数据点x0，前向扩散过程产生一个序列x1, x2,..., xT，其中每个xt都是通过在 $x_{t-1}$ 上添加高斯噪声得到的。

2.2 反向生成过程

在这个阶段，diffusion model通过反向去噪过程，从噪声图像noise中逐步生成新的样本，这个过程是前向过程的逆过程，model学会每一步都剔除一些模拟高斯噪声，让图像变得更清晰。
给定一个最中的噪声图像数据noise xT，反向过程生成一个序列 $x_{T-1}, x_{T-2},..., x_0$ ，最终得到一个新的数据样本。
Diffusion model training的目的是学习一个精准的去噪网络，可在每一步准确地预估需要剔除的模拟高斯噪声 $\epsilon_{\theta}$ ，使纯噪声图像noise能够在反向过程中生成高质量的新样本。

2.3 Diffusion model优缺点

优点是扩散模型能生成样本质量高且多样性强的新图像。
缺点是计算代价较高，因为生成过程需要执行多次去噪操作。

3. DDPM Formulation Derivation

3.1 前向过程

在前向过程中，从训练集真实图像中随机采样一张图像 $x_0$ 会被添加T次噪声，使最终噪声图像 $x_T$ 符合标准正态分布。那么前向过程 $q(x_t|x_{t-1})$ 指的是在前向的每一步通过向图像 $x_{t-1}$ 中添加高斯噪声 $\epsilon$ 得到 $x_t$ 。 $x_t$ 是从一个均值与 $x_{t-1}$ 相关的正态分布里采样出来的，不是无脑地直接相加，这是一个马尔可夫过程， $x_t$ 状态只与上一个状态 $x_{t-1}$ 相关，过程表示为:

$x_t \sim \mathcal{N} (\mu_t(x_{t-1}), \sigma^2_tI)$

这个正态分布还可以写成公式(1-1)变体形式：

$x_t \sim \mathcal{N}(\sqrt{1-\beta_t}x_{t-1}, \beta_tI)$

这个公式看起来很奇怪，主要是 $\sqrt{1-\beta_t}$ 这个系数是从哪冒出来的？

证明：归纳法--假定这个公式是正确的，从结论出发倒推，证明假设或公式正确。假如给定 $x_0$ ，也就是从训练数据集里采样出一幅图片，那么该怎么计算任意时刻t的图像 $x_t$ 呢？

我们根据上式从 $x_t$ 开始倒推， $x_t$ 是一个接近服从正态分布的样本，假设正向过程加入的高斯噪声为 $\epsilon_t$ ，很明显 $\epsilon_t$ 也服从正态分布， $\epsilon_t \sim \mathcal{N}(0,I)$ 。那么对应加入上一时刻图像 $x_{t-1}$ 的高斯噪声为 $\epsilon_{t-1}$ ，可以推出加噪公式(1):

$x_t = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t} \epsilon_{t-1}$ (1)

再往前推几步：

$x_t = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t} \epsilon_{t-1} \\ = \sqrt{1-\beta_t}(\sqrt{1-\beta_{t-1}}x_{t-2} + \sqrt{\beta_{t-1}}\epsilon_{t-2}) + \sqrt{\beta_t} \epsilon_{t-1} \\ = \sqrt{(1-\beta_t)(1-\beta_{t-1})} x_{t-2} + \sqrt{(1-\beta_t)\beta_{t-1}}\epsilon_{t-2}+ \sqrt{\beta_t} \epsilon_{t-1}$

从正态分布性质可知: 均值相同的正态分布加在一起后，方差也会加到一起，也就是 $\mathcal{N}(0, \sigma_1^2 I)$ 与 $\mathcal{N}(0, \sigma_2^2 I)$ 合起来会得到 $\mathcal{N}(0, (\sigma_1^2 + \sigma_1^2) I)$ 。根据这一性质， $\sqrt{(1-\beta_t)\beta_{t-1}}\epsilon_{t-2}+ \sqrt{\beta_t} \epsilon_{t-1}$ 这一项乘开、相加、化简为，可得：

$\sqrt{(1-\beta_t)(1-\beta_{t-1})} x_{t-2} + \sqrt{(1-\beta_t)\beta_{t-1}}\epsilon_{t-2}+ \sqrt{\beta_t} \epsilon_{t-1} \\ = \sqrt{(1-\beta_t)(1-\beta_{t-1})} x_{t-2} + \sqrt{1-(1-\beta_t)(1-\beta_{t-1})} \epsilon$

在往前推一步到t-2时刻，结果是：

$\sqrt{(1-\beta_t)(1-\beta_{t-1})(1-\beta_{t-2})} x_{t-3} + \sqrt{1-(1-\beta_t)(1-\beta_{t-1})(1-\beta_{t-2})} \epsilon$

这时我们令 $\alpha_t=1-\beta_t$ , $\bar{\alpha_t} = \prod^{t}_{i=1}\alpha_i$ ，可以很容易的总结出加噪公式(2)：

$x_t = \sqrt{\bar{\alpha_t}}x_0 + \sqrt{1-\bar{\alpha_t}} \epsilon$ (2)

这里， $\beta_t$ 是一个小于1的常数，并且从几乎为0开始逐渐增大，这时 $\alpha_t$ 逐渐变小， $\bar{\alpha_t}$ 趋近于0的速度也越来越快。最后 $\bar{\alpha_T}$ 几乎为0，带入公式(2)： $x_T = \sqrt{\bar{\alpha_T}}x_0 + \sqrt{1 - \bar{\alpha_T}}\epsilon$ 就满足标准正态分布里，符合我们对扩散模型的需求，自然证明 $x_t \sim \mathcal{N}(\sqrt{1-\beta_t}x_{t-1}, \beta_tI)$ 满足正态分布。

上述推断可以简单描述为：加噪公式能够从慢到快地改变原始图像 $x_0$ ，让图像 $x_t$ 最终均值为0，方差为I。