数据结构5---矩阵和广义表

news2024/11/27 10:27:50

一、矩阵的压缩存储

特殊矩阵:矩阵中很多值相同的元素并且它们的分布有一定的规律。

稀疏矩阵:矩阵中有很多零元素。压缩存储的基本思想是:

        (1)为多个值相同的元素只分配一个存储空间;

        (2)对零元素不分配存储空间。

1、特殊矩阵的压缩存储

（1）对称矩阵

只存储下三角部分的元素

存储结构

对于下三角的元素aij(i>=j)，在数组中的下标与i,j关系为 k = i*(i-1)/2 + j-1

上三角的元素aij(i<j),因为aij = aji，则访问它的元素aji即可,即：k = j*(j-1)/2+i - 1

 (2)三角矩阵

只存储上三角(或下三角)部分的元素

下三角矩阵

存储：

1.下三角元素        2.对角线上方的常数

矩阵中的任一元素aij在数组中的下标k与i,j的对应关系

当i>=j时        k=i*(i-1)/2+j-1

当i<j              k=n*(n+1)/2

上三角矩阵

存储：

1.上三角元素        2.对角线下方的常数

矩阵中的任一元素aij在数组中的下标k与i,j的对应关系

当i<=j时        k=(i-1)*(2n-i+2)/2+j-1

当i>j              k=n*(n+1)/2

 (3)对角矩阵

对角矩阵:所有非零元素都集中在以主对角线为中心的带状区域中，除了主对角线和它的上下方若干条对角线的元素外，所有其他元素都为零。

 (4)稀疏矩阵

 我们定义了一个三元组

struct Triple
{
    int row,col;    //行和列
    DataType item;    //值
};

三元组表:将稀疏矩阵的非零元素对应的三元组所构成的集合,按行优先的顺序排列成一个线性表。

采用顺序存储结构存储三元组表

三元顺序表的存储结构定义

const int MAX = 100;
struct SparseMatrix
{
    struct Triple data[MAX];    //存储非零元素
    int mu,nu,num;    //行数，列数，非零元素个数
};

这种存储方法的缺点是:进行矩阵加法、减法等操作时，非零元素的个数和位置都会发生变化，顺序存储法就非常不方便了。

2、十字链表

采用链接存储结构存储三元组表，每个非零元素对应的三元组存储为一个链表结点，结构为:

rowcolitem
downright

row:存储非零元素的行号

col:存储非零元素的列号

item:存储非零元素的值

right:指针域，指向同一行中的下一个三元组

down:指针域，指向同一列中的下一个三元组

定义结构体

#define ElementType int
 
typedef struct OLNode
{
    int row;//1~m
    int col;//1~n
    ElementType value;
    struct OLNode *right, *down;//非零元素所在行，列后继链域
}OLNode, *OLink;
 
typedef struct CrossList
{
    OLink* row_head, *col_head;//行，列链表的头指针向量
    int m;//行数
    int n;//列数
    int len;//非零元素个数
}CrossList;

代码实现

//稀疏矩阵的链式存储结构：十字链表
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
 
#define ElementType int
 
typedef struct OLNode
{
    int row;//1~m
    int col;//1~n
    ElementType value;
    struct OLNode *right, *down;//非零元素所在行，列后继链域
}OLNode, *OLink;
 
typedef struct CrossList
{
    OLink* row_head, *col_head;//行，列链表的头指针向量
    int m;//行数
    int n;//列数
    int len;//非零元素个数
}CrossList;
 
void CreatCrossList(CrossList* M, int m, int n, int len)
{
    M->m = m;
    M->n = n;
    M->len = len;
    if(!(M->row_head = (OLink*)malloc((m + 1) * sizeof(OLink))))
    {
        perror("row_head");
        exit(-1);
    }
    if(!(M->col_head = (OLink*)malloc((n + 1) * sizeof(OLink))))
    {
        perror("col_head");
        exit(-1);
    }
    memset(M->row_head, 0, (m + 1) * sizeof(OLink));
    memset(M->col_head, 0, (n + 1) * sizeof(OLink));//初始化为空链表
 
    int i = 0, j = 0, e = 0;//结点的行，列，值
    printf("请输入结点的行号,列号,值:\n");
    while(len)
    {
        scanf("%d %d %d", &i, &j, &e);
        if(i < 1||i > m||j < 1||j > n)
        {
            printf("行列号不合法,请重新输入:\n");
            continue;
        }
 
        int flag = 0;//检查位置是否重复
        for(OLNode* k = M->row_head[i]; k != NULL; k = k->right)
        {
            if(k->col == j)
            flag = 1;
        }
        if(flag)
        {
            printf("结点位置重复,请重新输入:\n");
            continue;
        }
 
        OLNode* p = (OLNode*)malloc(sizeof(OLNode));//申请结点
        if(p == NULL)
        {
            perror("Node application");
            exit(-1);
        }
        p->row = i; p->col = j; p->value = e;
        p->right = p->down = NULL;
 
        //行链表插入
        if(M->row_head[i] == NULL)//该行还没有结点
        {
            M->row_head[i] = p;
        }
        else if(p->col < M->row_head[i]->col)//新建结点列号<该行首结点列号
        {
            p->right = M->row_head[i];
            M->row_head[i] = p;
        }
        else//寻找插入位置
        {
            OLNode* q;
            for(q = M->row_head[i]; q->right && q->right->col < j; q = q->right);
            p->right = q->right;
            q->right = p;
        }
 
        //列链表插入
        if(M->col_head[j] == NULL)//该列还没有结点
        {
            M->col_head[j] = p;
        }
        else if(p->row < M->col_head[j]->row)//新建结点行号<改行首节点行号
        {
            p->down = M->col_head[j];
            M->col_head[j] = p;
        }
        else//寻找插入位置
        {
            OLNode* q;
            for(q = M->col_head[j]; q->down && q->down->row < i; q = q->down)
            p->down = q->down;
            p->down = p;
        }
 
        len--;
        printf("插入成功!\n");
        printf("请输入结点的行号,列号,值:\n");
    }
 
}
 
void PrintCrossList(CrossList* M)//打印十字链表
{
    for(int row = 0; row < M->m; row++)
    {
        OLNode* p = M->row_head[row];
        while(p != NULL)
        {
            printf("(%d, %d)=%d ", p->row, p->col, p->value);
            p = p->right;
        }
        printf("\n");
    }
}
 
int main()
{
    CrossList M;
    CreatCrossList(&M, 10, 10, 10);
    PrintCrossList(&M);
    return 0;
}

3、快速转置

在顺序结构里转置

(1)简单转置

按矩阵source的列序进行转置

算法实现

SparseMatrix source,dest;
int q = 1;
for(col=1;col<=source.nu;col++)
{
    for(p=1;p<=source.num;p++){
        if(source.data[p].col==col)
            {
                dest.data[q].row = source.data[p].col;
                dest.data[q].col = source.data[p].row;
                dest.data[q].e = source.data[p].e;
                q++;
            }
        }
   }

(2)快速转置

按矩阵source的行序进行转置

方法：增加2个辅助向量

这里的cPos[col]为：1 3 5 7 8 8 9

-3一定是第一个，12一定是第三个....

cPos算法:

cPos[1] = 1;
for(col = 2;col <= source.nu; col++)
{
    cPos[col] = cPos[col-1]+cNum[col-1];
}

cNum算法：

for(col = 1;col <= source.nu; ++col) cNum[col]=0;    //初始化全为0
for(sPos = 1;sPos <= source.number;++sPos)
    ++cNum[source.data[sPos].col];        //就是按列遍历整个三元组，列号为几，就在对应的cNum上++

就是找位置，找到对应位置后，其相应的cPs+1

二、广义表

1、定义

 广义表又称列表，也是一种线性存储结构，通数组类似，广义表中即可存储不可再分的元素也能存储可在分元素。

        例如：数组中可以存储‘a’、3这样的字符或数字，也能存储数组，比如二维数组、三维数组，数组都是可在分成子元素的。广义表也是如此，但与数组不同的是，在广义表中存储的数据是既可以再分也可以不再分的，形如：{1,{1,2,3}}。

    广义表记作：

LS = (a1,a2,…,an)

2、原子和子表

    广义表中存储的单个元素称为 "原子"，而存储的广义表称为 "子表"。

例如创建一个广义表 LS = {1,{1,2,3}}，我们可以这样解释此广义表的构成：广义表 LS 存储了一个原子 1 和子表 {1,2,3}。

以下是广义表存储数据的一些常用形式：

  • A = ()：A 表示一个广义表，只不过表是空的。
  • B = (e)：广义表 B 中只有一个原子 e。
  • C = (a,(b,c,d)) ：广义表 C 中有两个元素，原子 a 和子表 (b,c,d)。
  • D = (A,B,C)：广义表 D 中存有 3 个子表，分别是A、B和C。这种表示方式等同于 D = ((),(e),(b,c,d)) 。
  • E = (a,E)：广义表 E 中有两个元素，原子 a 和它本身。这是一个递归广义表，等同于：E = (a,(a,(a,…)))。


注意，A = () 和 A = (()) 是不一样的。前者是空表，而后者是包含一个子表的广义表，只不过这个子表是空表。

3、表头和表尾

当广义表不是空表时，称第一个数据（原子或子表）为"表头"，剩下的数据构成的新广义表为"表尾"。

强调一下，除非广义表为空表，否则广义表一定具有表头和表尾，且广义表的表尾一定是一个广义表。

例如在广义表中 LS={1,{1,2,3},5} 中，表头为原子 1，表尾为子表 {1,2,3} 和原子 5 构成的广义表，即 {{1,2,3},5}。

再比如，在广义表 LS = {1} 中，表头为原子 1 ，但由于广义表中无表尾元素，因此该表的表尾是一个空表，用 {} 表示。

4、广义表的存储结构

使用顺序表实现广义表结构，不仅需要操作 n 维数组（例如 {1,{2,{3,4}}} 就需要使用三维数组存储），还会造成存储空间的浪费。

typedef struct GLNode{
    int tag;//标志域
    union{
        char atom;//原子结点的值域
        struct{
            struct GLNode * hp,*tp;
        }ptr;//子表结点的指针域，hp指向表头；tp指向表尾
    }subNode;
}*Glist;

 这里用到了 union 共用体，因为同一时间此节点不是原子节点就是子表节点，当表示原子节点时，就使用 atom 变量；反之则使用 ptr 结构体。

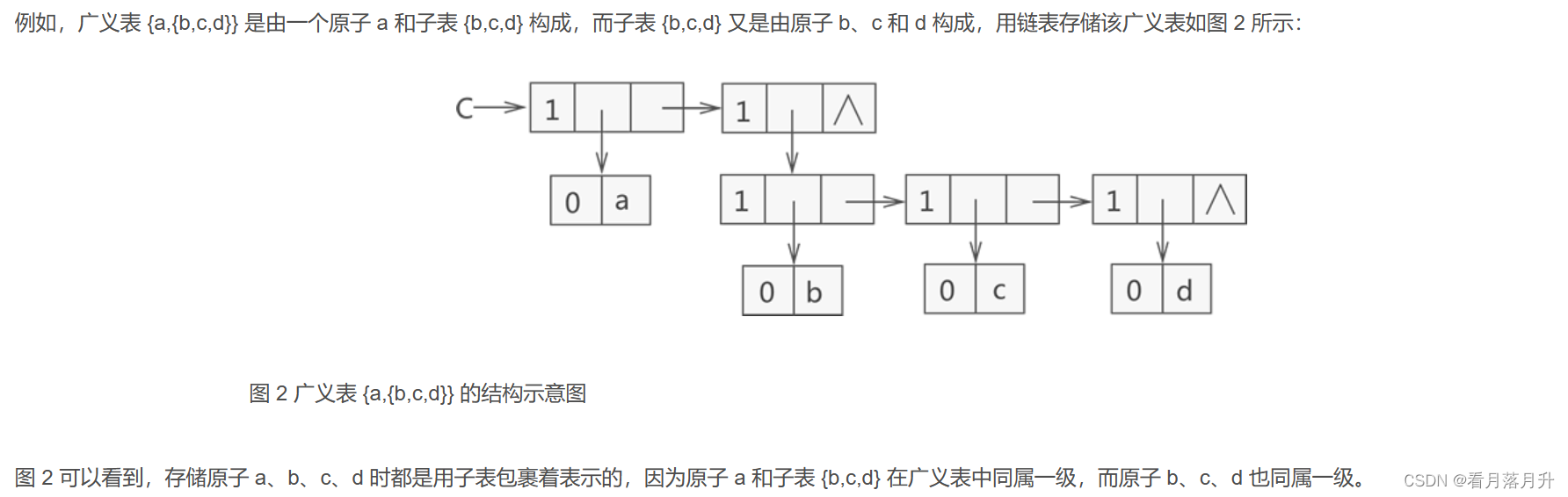
Glist creatGlist(Glist C) {
    //广义表C
    C = (Glist)malloc(sizeof(Glist));
    C->tag = 1;
    //表头原子‘a’
    C->subNode.ptr.hp = (Glist)malloc(sizeof(Glist));
    C->subNode.ptr.hp->tag = 0;
    C->subNode.ptr.hp->subNode.atom = 'a';
    //表尾子表（b,c,d）,是一个整体
    C->subNode.ptr.tp = (Glist)malloc(sizeof(Glist));
    C->subNode.ptr.tp->tag = 1;
    C->subNode.ptr.tp->subNode.ptr.hp = (Glist)malloc(sizeof(Glist));
    C->subNode.ptr.tp->subNode.ptr.tp = NULL;
    //开始存放下一个数据元素（b,c,d）,表头为‘b’，表尾为（c,d）
    C->subNode.ptr.tp->subNode.ptr.hp->tag = 1;
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.hp = (Glist)malloc(sizeof(Glist));
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.hp->tag = 0;
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.hp->subNode.atom = 'b';
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp = (Glist)malloc(sizeof(Glist));
    //存放子表(c,d)，表头为c，表尾为d
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->tag = 1;
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.hp = (Glist)malloc(sizeof(Glist));
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.hp->tag = 0;
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.hp->subNode.atom = 'c';
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.tp = (Glist)malloc(sizeof(Glist));
    //存放表尾d
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.tp->tag = 1;
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.tp->subNode.ptr.hp = (Glist)malloc(sizeof(Glist));
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.tp->subNode.ptr.hp->tag = 0;
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.tp->subNode.ptr.hp->subNode.atom = 'd';
    C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.tp->subNode.ptr.tp = NULL;
    return C;
}

4、长度 

 广义表的长度，指的是广义表中所包含的数据元素的个数。
由于广义表中可以同时存储原子和子表两种类型的数据，因此在计算广义表的长度时规定，广义表中存储的每个原子算作一个数据，同样每个子表也只算作是一个数据。
例如，在广义表 {a,{b,c,d}} 中，它包含一个原子和一个子表，因此该广义表的长度为 2。
再比如，广义表 {{a,b,c}} 中只有一个子表 {a,b,c}，因此它的长度为 1。
前面我们用 LS={a1,a2,...,an} 来表示一个广义表，其中每个 ai 都可用来表示一个原子或子表，其实它还可以表示广义表 LS 的长度为 n。

广义表规定，空表 {} 的长度为 0。

 5、深度

由于这个不做考试内容，分享一个博客

数据结构-广义表-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/qq_51701007/article/details/126352030?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522171894059816800211521274%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=171894059816800211521274&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-126352030-null-null.142%5Ev100%5Epc_search_result_base5&utm_term=%E5%B9%BF%E4%B9%89%E8%A1%A8&spm=1018.2226.3001.4187

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1848701.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

vue3爷孙组件通信——provide和inject

vue3爷孙组件通信——provide和inject

父组件中提供数据&#xff0c;并在子组件中注入这些数据&#xff0c;从而实现了组件之间的数据传递。可用于兄弟组件通信&#xff0c;爷孙组件通信&#xff0c;父子通信。 provide( ‘注入名’, 注入值" ) 和 inject(‘注入名’) 第一代组件&#xff1a; <template>…
阅读更多...
【干货】微信小程序免费开源项目合集

【干货】微信小程序免费开源项目合集

前言 2024年了&#xff0c;还有小伙伴在问微信小程序要怎么开发&#xff0c;有什么好的推荐学习项目可以参考的。今天分享一个收集了一系列在微信小程序开发中有用的工具、库、插件和资源&#xff1a;awesome-github-wechat-weapp。 开源项目介绍 它提供了丰富的资源列表&…
阅读更多...
研究人员描述了如何判断ChatGPT是否在虚构

研究人员描述了如何判断ChatGPT是否在虚构

研究人员描述了如何判断ChatGPT是否在虚构 这是世界上最不为人知的秘密之一&#xff0c;大型语言模型对查询给出了明显错误的答案&#xff0c;并自信地这样做&#xff0c;与它们正确的时候没有区别。这有很多原因。人工智能可能已经接受了错误信息的训练;答案可能需要从LLM无法…
阅读更多...
c++ virtual || virtual =0

c++ virtual || virtual =0

抽象类 && 继承 抽象类&#xff1a;包含纯虚函数的类称为抽象类&#xff0c;继承层次结构的较上层。作用&#xff1a;将有关的操作作为结果接口组织在一个继承层次结构中&#xff0c;由它来为派生类提供一个公共的根&#xff0c;派生类将具体实现在其基类中作为接口的…
阅读更多...
Spring Clude 是什么？

Spring Clude 是什么？

目录 认识微服务 单体架构 集群和分布式架构 集群和分布式 集群和分布式区别和联系 微服务架构 分布式架构&微服务架构 微服务的优势和带来的挑战 微服务解决方案- Spring Cloud 什么是 Spring Cloud Spring Cloud 版本 Spring Cloud 和 SpringBoot 的关系 Sp…
阅读更多...
实验一：Ubuntu系统中的USB设备绑定实验

实验一：Ubuntu系统中的USB设备绑定实验

实验一&#xff1a;Ubuntu系统中的USB设备绑定实验 一、实验目的二、实验原理三、实验环境四、实验步骤任务 1&#xff1a;绑定不同USB设备任务 2&#xff1a;绑定多个相同设ID的串口设备 五、注意事项六、拓展练习 一、实验目的 学习Ubuntu中USB设备命名方法&#xff1b;掌握…
阅读更多...
如何选择优质智慧公厕系统厂家？@光明源

如何选择优质智慧公厕系统厂家？@光明源

随着智慧城市建设的推进&#xff0c;智慧公厕系统成为提升城市公共服务水平的重要一环。选择一家优质的智慧公厕系统厂家不仅能确保设备的先进性和可靠性&#xff0c;还能提升用户体验和管理效率。以下是选择优质智慧公厕系统厂家的关键要素。 1. 厂家资质和信誉 1.1 资质认证…
阅读更多...
AI/ML 数据湖参考架构架构师指南

AI/ML 数据湖参考架构架构师指南

这篇文章的缩写版本于 2024 年 3 月 19 日出现在 The New Stack 上。 在企业人工智能中&#xff0c;主要有两种类型的模型&#xff1a;判别模型和生成模型。判别模型用于对数据进行分类或预测&#xff0c;而生成模型用于创建新数据。尽管生成式人工智能最近占据了新闻的主导地…
阅读更多...
WordPress如何删除前端评论中的网址字段？

WordPress如何删除前端评论中的网址字段？

前面跟大家分享的『WordPress插件Comment Link Remove and Other Comment Tools&#xff0c;删除评论网址字段』一文&#xff0c;通过安装插件可轻松删除前端评论中的网址字段&#xff0c;不过有些站长不喜欢安装插件&#xff0c;那么是否可以通过纯代码去掉网址字段呢&#xf…
阅读更多...
大数据与java哪个好找工作？这篇文章帮你做选择！

大数据与java哪个好找工作？这篇文章帮你做选择！

大数据与java哪个好找工作&#xff1f;这篇文章帮你做选择&#xff01; 还在为选择Java开发还是Java大数据而头疼吗&#xff1f;别担心&#xff0c;本文将从就业前景、学习方向、学习内容以及薪资待遇四个方面&#xff0c;为你揭开Java和Java大数据的神秘面纱&#xff0c;帮你做…
阅读更多...
安卓设备优雅的命令 adb 以及 优秀的控制 scrcpy

安卓设备优雅的命令 adb 以及 优秀的控制 scrcpy

一、背景 如果有多台安卓设备&#xff0c;并为这些设备安装软件&#xff0c;一个个使用u盘再加上鼠标操作虽然可以做到&#xff0c;但是大概率比较麻烦。试想下&#xff0c;如果坐在电脑旁边&#xff0c;就能鼠标在电脑上点点就能解决问题&#xff0c;是多么优雅的一件事情。 …
阅读更多...
【单片机】Code Composer Studio Linux版本下载，CCS开发环境

【单片机】Code Composer Studio Linux版本下载，CCS开发环境

被windows的驱动兼容性搞得烦死了&#xff0c;我直接搞虚拟机用linux版本的ccs尝试一下。 下载&#xff1a; https://www.ti.com/tool/download/CCSTUDIO ubuntu22 虚拟机内&#xff0c;安装一些依赖&#xff1a; 安装libc6-i386库&#xff1a; 运行以下命令来安装libc6-i38…
阅读更多...
鞠婧祎多个商标被丝芭传媒申请注册！

鞠婧祎多个商标被丝芭传媒申请注册！

近日鞠婧祎与丝芭传媒合约引发网络关注&#xff0c;普推商标老杨经检索发现&#xff0c;丝芭传媒早在2016起就申请注册了“鞠婧祎”24个商标&#xff0c;涉及多个商标分类&#xff0c;这些基本都下商标注册证。 不管对经纪公司还是网红公司&#xff0c;有实力的基本都会对旗下的…
阅读更多...
分布式光纤测温DTS在工程现场中稳定性与可靠性如何？

分布式光纤测温DTS在工程现场中稳定性与可靠性如何？

20年前&#xff0c;分布式光纤测温(Distributed Temperature Sensing&#xff0c;DTS)技术的发展尚不成熟&#xff0c;设备成本高昂&#xff0c;其稳定性与可靠性也存在一定问题。然而&#xff0c;经过二十多年的不断发展与创新&#xff0c;DTS技术在工程现场应用中取得了显著进…
阅读更多...
晶体振荡电路中的负性阻抗是什么？-晶发电子

晶体振荡电路中的负性阻抗是什么？-晶发电子

在理想的振荡电路中&#xff0c;为了保持振荡的稳定性和强度&#xff0c;需要一种机制来补偿晶振振动过程中的能量损耗。在实际应用中&#xff0c;这种能量损耗是不可避免的&#xff0c;它可能导致振荡逐渐衰减直至停止。为了解决这个问题&#xff0c;振荡电路设计者采用了一种…
阅读更多...
【CV炼丹师勇闯力扣训练营 Day8】

【CV炼丹师勇闯力扣训练营 Day8】

CV炼丹师勇闯力扣训练营 代码随想录算法训练营第8天 ● 344.反转字符串 ● 541. 反转字符串II ● 卡码网&#xff1a;54.替换数字 一、344 反转字符串 编写一个函数&#xff0c;其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。 不要给另外的数组分配额…
阅读更多...
天马学航——智慧教务系统(移动端)开发日志四

天马学航——智慧教务系统(移动端)开发日志四

天马学航——智慧教务系统(移动端)开发日志四 日志摘要&#xff1a;优化了教师端界面的UI&#xff0c;更新了教师端添加课程&#xff0c;提交成绩等功能&#xff0c;修复了一些已知的BUG 1、教师添加课程设计 教师在此界面添加课程&#xff0c;并将数据提交后端进行审核 界…
阅读更多...
【STM32-MAP文件分析】

【STM32-MAP文件分析】

STM32-MAP文件分析 ■ MDK编译生成文件简介■ .o■ .axf■ .hex■ .crf■ .d■ .dep■ .lnp■ .lst■ .map■ .build_log.htm■ .htm 文件■ .map 文件 ■ map文件分析■ map 文件的 MDK 设置■ 1. 要生成 map 文件 在 Listing 选项卡里面■ 2. Keil5 中打开.map 文件 ■ map 文…
阅读更多...
如何用GO语言实现冒泡排序算法？

如何用GO语言实现冒泡排序算法？

本章教程，介绍一下如何用GO语言实现基础排序算法中的冒泡排序。 一、程序代码 package mainimport ("fmt""math/rand""time" )// bubbleSort 函数实现冒泡排序算法 func bubbleSort(arr []int) {n
阅读更多...
【面试干货】 Java 中的 HashSet 底层实现

【面试干货】 Java 中的 HashSet 底层实现

【面试干货】 Java 中的 HashSet 底层实现 1、HashSet 的底层实现2、 HashSet 的特点3、 总结 &#x1f496;The Begin&#x1f496;点点关注&#xff0c;收藏不迷路&#x1f496; HashSet 是 Java 集合框架中的一个重要成员&#xff0c;它提供了不存储重复元素的集合。但是&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023