1889:【提高】多重背包(2)
二维费用背包
2075 - 最大卡路里
1928 - 采购礼品
感谢

| 背包容量:(c) | 6 |
| 重量 | weight | 2 | 2 | 4 | 6 | 2 |
| 1 | 2 | 3 | 4 | 5 | ||
| 价值 | value | 3 | 6 | 5 | 5 | 8 |
| 1 | 2 | 3 | 4 | 5 |
| w | v | |||||||
| dp数组: | 记录有i件物品,背包容量为j的情况下,最大价值 | |||||||
| name | weight | value | 1 | 2 | 3 | 4 | 5 | 6 |
| a | 2 | 3 | 0 | 3 | 3 | 3 | 3 | 3 |
| b | 2 | 6 | 0 | 6 | /6 | 6+dp[i-1][j-w[i]]=9 | 9 | 9 |
| c | 4 | 5 | ||||||
| d | 6 | 5 | ||||||
| e | 2 | 8 | ||||||
第i件物品
w[i]>c:放不下,最大价值=i-1件物品讨论时的最大价值
选:剩余容量=c-w[i],最大价值=v[i]+(i-1件物品,容量在 c-w[i]的情况下最大价值)
w[i]<=c:放得下
不选:最大价值=i-1件物品讨论时的最大价值
dp[i][j]
w[i]>c:放不下,最大价值 =dp[i-1][j]
选,最大价值 =v[i]+ dp[i-1][c--w[i]]
w[i]<=c:放得下,最大价值
不选,最大价值 =dp[i-1][j]
动态转移方程:
dp[i][j]=max(dp[i-1][j],v[i]+dp[i-1][j-w[i]])
1889:【提高】多重背包(2)
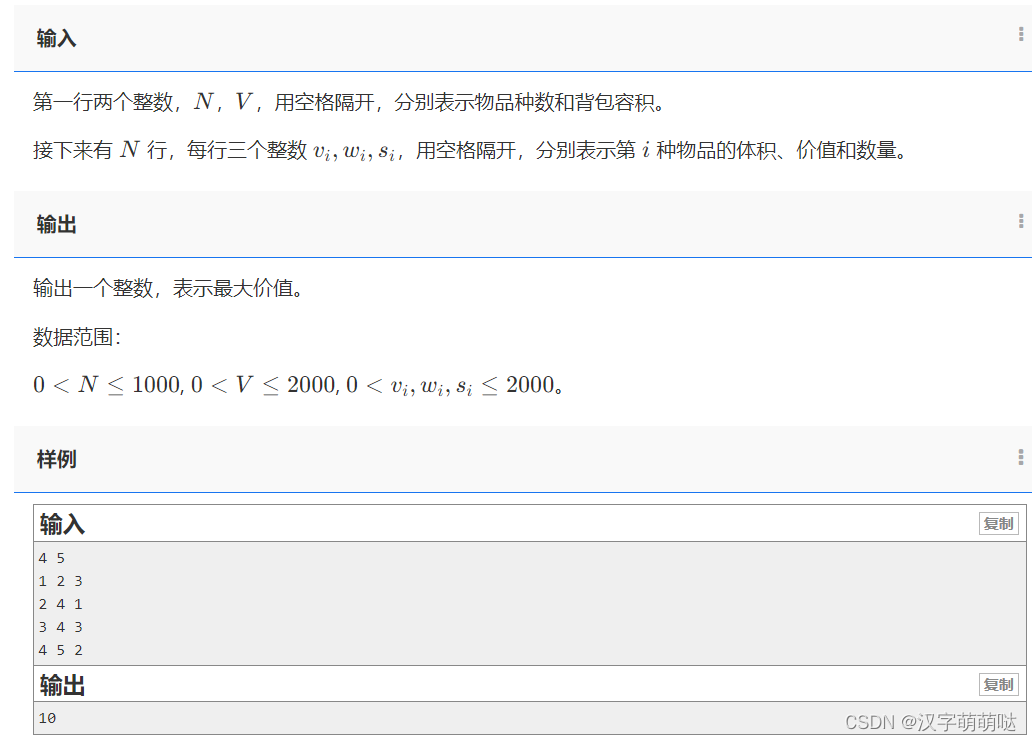
题目描述
有 N 种物品和一个容量是 V的背包。
第 ii种物品最多有 si 件,每件体积是 vi,价值是 wi 。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
关于 DP要理解的关键点:
1 、DP的本质
求有限的集合中的最值(个数)
本质上,DP代表了走到阶段i 的所有路线的最优解;
2 、DP需要思考的点:
(1)DP 的状态是什么?状态要求什么:最大、最小、数量?
(2)DP 的状态计算?
状态转义方程;
求解方法: a 、递推 b、考虑阶段i (最后一个阶段的值)的值是如何得来的;
(3)DP 的边界是什么?
关键术语:阶段、状态、决策(状态转移方程)、边界;
以数塔问题(1216:【基础】数塔问题)为例,理解DP 的本质,再理解01背包的本质 (1282:【提高】简单背包问题);
经典的 DP模板题要熟练掌握,熟记状态转义方程!
本题解题的关键点:二进制优化(类似压缩的思想)
( 1 ) 有n 个不同的物品,要讨论2"种选择的可能(每个物品选或者不选);
(2)一个物品有n 件,虽然要讨论2"种选择的可能,但由于n 个物品是一样的,那么 就减少了讨论数量,比如:有4个物品,如果是不同物品的选2个,选12、23是不同的 选择,但如果是相同的物品,选哪两个就都是一样的了。
因此,n 个物品,要讨论的可能就分别是:选0个、选1个、选2个、选3个…选n 个。 (3)要将0~n 个不同的选择表达出来,比较简单的方法是将n 二进制化。
比如:整数7,只需要用124三个数任意组合,就能组合出0~7这8种可能。
再比如:整数10,只需要用1243(注意最后一个数),就能组合出0~10这11种可 能,这样 n 这个值就被二进制化了。
因此如果要讨论10个一样的物品,就转化为讨论4个不同的物品了;而n 个一样的物 品,就转化为log₂n 个不同的物品进行讨论。
dp[j]=max{dp[j],dp[j-w[i]]+v[i]}
#include <bits/stdc++.h>
using namespace std;
const int N=20010;
int v[N],w[N],dp[2010];
int n,m;//n种物品,背包容量为m
int vi,wi,si;
int k=0;
int main() {
cin>>n>>m;
for(int i=1; i<= n; i++) {
cin>>vi>>wi>>si;
/*对si二进制化,比如:
有10件一样的物品我们转换为有4件不同的物品:1 2 4 3
这4种物品的体积分别是:1*vi 2*vi 4*vi 3*vi*/
int t=1;//权重,表示2的次方
while(t<= si) {
k++;
v[k]= t* vi;
w[k]=t* wi;
si =si-t;
t=t*2;
}
//如果二进制化有剩余,存入
if(si >0) {
k++;
v[k]= si * vi;
w[k]= si * wi;
}
}
//01 背包
for(int i=1; i<= k; i++) {
for(int j= m; j >= v[i]; j--) {
dp[j]= max(dp[j],dp[j-v[i]]+w[i]);
}
}
cout<<dp[m];
return 0;
}二维费用背包
二维费用的背包问题是指:对于每件物品,具有两种不同的费用;选择这件物品必须同 时付出这两种代价;对于每种代价都有一个可付出的最大值(背包容量)。问怎样选择物品 可以得到最大的价值。设这两种代价分别为代价1和代价2,第i 件物品所需的两种代价分 别 为v[i] 和 w[i]。
两种代价可付出的最大值(两种背包容量)分别为maxv 和 maxw, 物品的价值为c[i]。
解决方法: 费用加了一维,只需状态也加一维即可。
设 f[i][j][k] 表示前i 件物品付出两种代价分别,背包体积为j, 背包的承重为k 时可
获得的最大价值。
状态转移方程就是:
f[i][j][k]=max(f[i-1][j][k],f[i-1][j-v[i]][k-w[i]]+c[i])
空间优化后,可以用二维数组求解。
f[j][k]=max(f[j][k],f[j-v[i]][k-w[i]]+c[i])
2075 - 最大卡路里
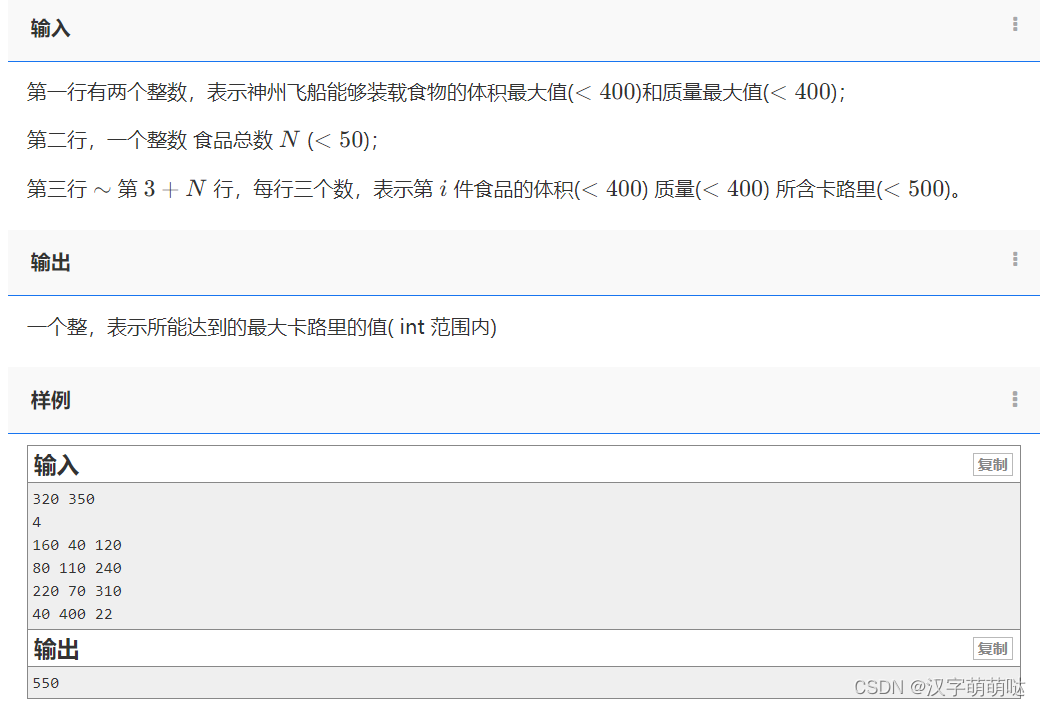
题目描述
神州飞船准备运送一批食品到太空站,该飞船能够运送食品的重量、体积都有严格的限制。
现已知 nn 件完全不同的食品,每种食品的重量、体积及该食品能够提供的卡路里的值,请你编程计算出,该飞船最多能够运送多少卡路里的食物?
#include <bits/stdc++.h>
using namespace std;
const int N=410;
int dp[N][N];//代表求解体积为j,重量为k时能够得到的最大价值
int n,v,w,c;
int maxv,maxw;//背包的上限
int main() {
cin>>maxv>>maxw;
cin>>n;
for(int i=1; i<= n; i++) {
cin>>v>>w>>c;
//01 背包
//从最大体积~当前物品体积降序循环,同理重量也要降序循环
for(int j= maxv; j >= v; j--) {
for(int k=maxw; k >= w; k--) {
dp[j][k]= max(dp[j][k],dp[j-v][k-w]+c);
}
}
}
cout<<dp[maxv][maxw];//最大价值
return 0;
}1928 - 采购礼品
题目描述
王老师来到商店为同学们采购礼品。
这家店有 n 种礼品(编号是 1∼n ),每种礼品只有 1 件。老板为了促销,对礼品进行搭配销售,有关联性的礼品必须都要采购(奇怪的规定),比如 1 号礼品和 3号礼品搭配了,3 号和 8 号礼品搭配了,那么王老师想要买 1 号礼品的话,就需要把 3 号和 8 号礼品都买了。
现给定每种礼品的价钱和价值,请问在有限的钱 w 的情况下,能够买到礼品的最大价值是多少?
输入
第一行输入三个整数,n,m,w,表示有n 种礼品,m 个搭配和你现有的钱的数目。
第二行至 n+1 行,每行有两个整数,c、d,表示第 ii 种礼品的价钱和价值。(1≤c,d≤10^5)
第 n+2 至 n+1+m 行 ,每行有两个整数,u、v,表示 u 号礼品和 vv 号礼品是有关联的,已经形成搭配销售的关系。
数据范围:
1≤n,w≤10^4,0≤m≤5 *10^3。
输出
一行,表示可以获得的最大价值。
样例
输入
5 3 10 3 10 3 10 3 10 5 100 10 1 1 3 3 2 4 2
输出
1
典型的01背包,但要求同一组的物品都要购买。我们可以采用并査集将同一组有关系的礼品的价值、价格汇总到该集合的根节点上,这样就保证了一个集合中的礼品都购买的情况。
它解决的是在有限的预算 w 下,如何选择一组关联的礼品(根据提供的搭配信息),使得这些礼品的价值总和最大。
-
定义了几个数组:
f用于并查集,存储物品之间的关系;q和v分别存储物品的价钱和价值;dp用于动态规划,记录在给定背包容量下的最大价值。 -
首先通过并查集对具有关联关系的物品进行合并,确保在考虑搭配时,每个组合中的所有物品都被视为一个整体。
-
然后,遍历所有物品,如果某物品不是其自身的根节点,说明这个物品已经被包含在某个组合中,需要更新根节点的价钱和价值。
-
接着进行动态规划计算。从背包容量
w到每种物品的价钱(降序),尝试是否可以添加当前物品,如果可以,更新背包的最大价值。 -
最后,输出在给定预算
w下可以获得的最大价值。 -
王老师需要在有限的预算
w下,选择价值最高的礼品组合,但受到了一些特定的搭配规则影响,即如果一种礼品被选中,与其搭配的相关礼品也必须被同时购买。 -
具体步骤如下:
-
理解问题: 首先,我们需要知道每种礼品的价值(
d)和价格(c),以及哪些礼品之间存在强制搭配关系(由u和v表示)。这是一个二维背包问题,因为搭配关系限制了我们不能单独选择某件礼品。 -
模型构建: 可以考虑使用动态规划的方法,比如创建一个二维数组
dp[i][j],其中i代表剩余的预算,j代表剩余的可选礼品数量。dp[i][j]表示在剩余预算i和可以选择的礼品数量j下,能获得的最大价值。 -
状态转移: 对于每个礼品
k,有两种情况:选择它(增加价值d[k]但减少可用预算c[k]),或不选择它。根据这两种情况,更新dp数组。 -
处理搭配关系: 在更新
dp时,要考虑已有的搭配关系。如果礼品k与l搭配,意味着在包含k的情况下,l也会被强制选择。因此,我们需要更新dp时包括这种情况。 -
寻找最大价值: 最终的答案就是
dp[w][n],即在预算w和所有礼品都可选的情况下,能获得的最大价值。 -
输出结果: 返回计算得到的最大价值作为答案。
#include <bits/stdc++.h>
using namespace std;
int f[10100];//存储物品之间的关系
int q[10100],v[10100];//价钱、价值
int dp[10100];//以拥有的钱来定义背包容量
//查:查询元素的根
int find(int x) {
return f[x]==x?x:f[x]=find(f[x]);
}
//并:合并元素xy
void merge(int x,int y) {
int fx = find(x);
int fy = find(y);
if(fx != fy) {
f[fx]=fy;
}
}
int main() {
int n,m,w;
cin>>n>>m>>w;//n个物品的价钱和价值
for(int i = 1; i<= n; i++) {
cin>>q[i]>>v[i];
//并查集初始化
f[i]= i;
}
//m个物品的关系
int x,y;
for(int i = 1; i<= m; i++) {
cin>>x>>y;
merge(x,y);
}
//将有关系的物品合并到这组物品的根上司
for(int i = 1; i<= n; i++) {
//该物品不是根,则将价钱和价值都合并到根上
if(f[i] != i) {
q[find(i)]+=q[i];
v[find(i)]+=v[i];
//将该组物品的价钱和价值清零
q[i]=0;
v[i]=0;
}
}
//01背包计算结果
for(int i = 1; i <= n; i++) {
//从背包容量(有多少钱)~该物品的价钱降序
for(int j= w; j >= q[i]; j--) {
dp[j] = max(dp[j],dp[j-q[i]]+v[i]);
}
}
cout<<dp[w];
return 0;
}
感谢
如若本文对您的学习或工作有所启发和帮助,恳请您给予宝贵的支持——轻轻一点,为文章点赞;若觉得内容值得分享给更多朋友,欢迎转发扩散;若认为此篇内容具有长期参考价值,敬请收藏以便随时查阅。
每一次您的点赞、分享与收藏,都是对我持续创作和分享的热情鼓励,也是推动我不断提供更多高质量内容的动力源泉。期待我们在下一篇文章中再次相遇,共同攀登知识的高峰!