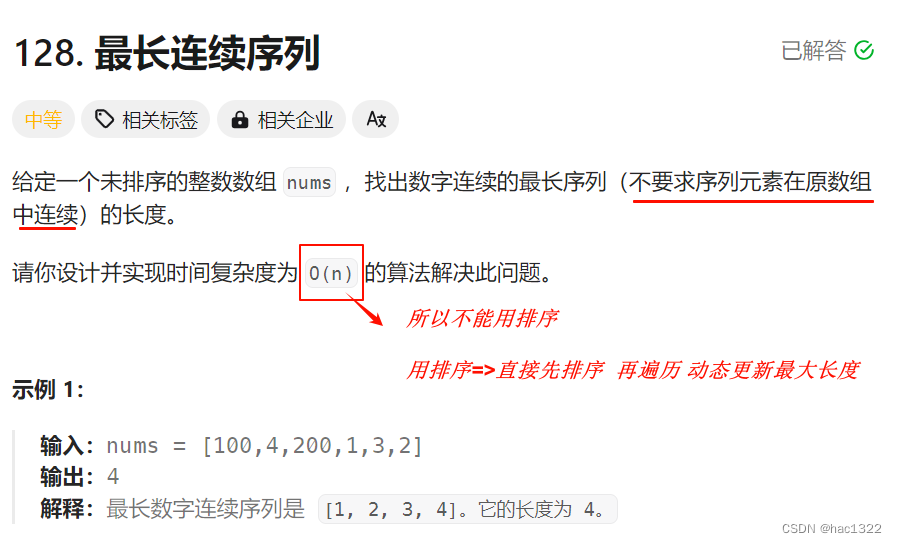
题目

原题链接：最长连续序列

题解

思路：

• 定义变量 res 用来记录最长连续序列的长度。
• 对集合中的每个元素进行如下处理：
  • 检查该元素是否是某个连续序列的起点（即 num - 1 不在集合中）。
  • 如果是序列的起点，则开始计算这个序列的长度：
    • 初始化一个计数器 cnt 为 1。
    • 使用 while 循环检查 num + 1 是否在集合中。如果在，则将 cnt 加 1，并将 num 增加 1。
  • 更新 res，使其始终保持最大值。

public class Test {
    public static int longestConsecutive(int[] nums) {
        if (nums == null || nums.length == 0) {
            return 0;
        }

        HashSet<Integer> set = new HashSet<>();
        for (int num : nums) {
            set.add(num);
        }
        int res = 0;
        for (Integer num : set) {
            if (!set.contains(num - 1)) {
                int cnt = 1;
                while (set.contains(num + 1)) {
                    cnt++;
                    num++;
                }
                res = Math.max(res, cnt);
            }
        }
        return res;
    }

    public static void main(String[] args) {
        int[] nums = {100, 4, 200, 1, 3, 2};
        System.out.println(longestConsecutive(nums));
    }
}

解释代码

内部条件检查
if (!numSet.contains(num - 1))

• 对于每个元素，我们检查它是否是一个序列的起点。
• 如果 num - 1 不在集合中，这意味着 num 是序列的起点。
• 每个元素最多被检查一次。

序列扩展（while循环）

while (set.contains(num + 1)) {
           cnt++;
           num++;
      }

• 只有当一个元素是序列的起点时，才会进入这个 while 循环。
• 从序列的起点开始，扩展这个序列，直到不能再扩展为止。

这个算法的时间复杂度是 O(n)，因为：

1. 哈希集合的构建是 O(n)。
2. 外层 for 循环遍历每个元素是 O(n)。
3. while 循环在整个算法过程中，每个元素最多被访问一次，总共也是 O(n)。（while里面最多会把每个元素遍历一次 eg：nums=[1,3,6,9,11] 所以O(n)）

时间复杂度别理解成了O(n²)

---

下面这个才是O(n²)，外层i加1，内层n次打印。(n*n)

  for (int i = 0; i < n; i++) {
      for (int j = 0; j < n; j++) {
         System.out.println("hello");
      }
  }

---

❤觉得有用的可以留个关注❤