🍭 大家好这里是清隆学长 ，一枚热爱算法的程序员

✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解

💻 ACM银牌🥈| 多次AK大厂笔试 ｜ 编程一对一辅导

👏 感谢大家的订阅➕ 和 喜欢💗

📎在线评测链接

https://app5938.acapp.acwing.com.cn/contest/2/problem/OD1072

🌍 评测功能需要 ⇒ 订阅专栏 ⇐ 后私信联系清隆解锁～

🍓OJ题目截图

🍿 5G基站光纤连接问题

问题描述

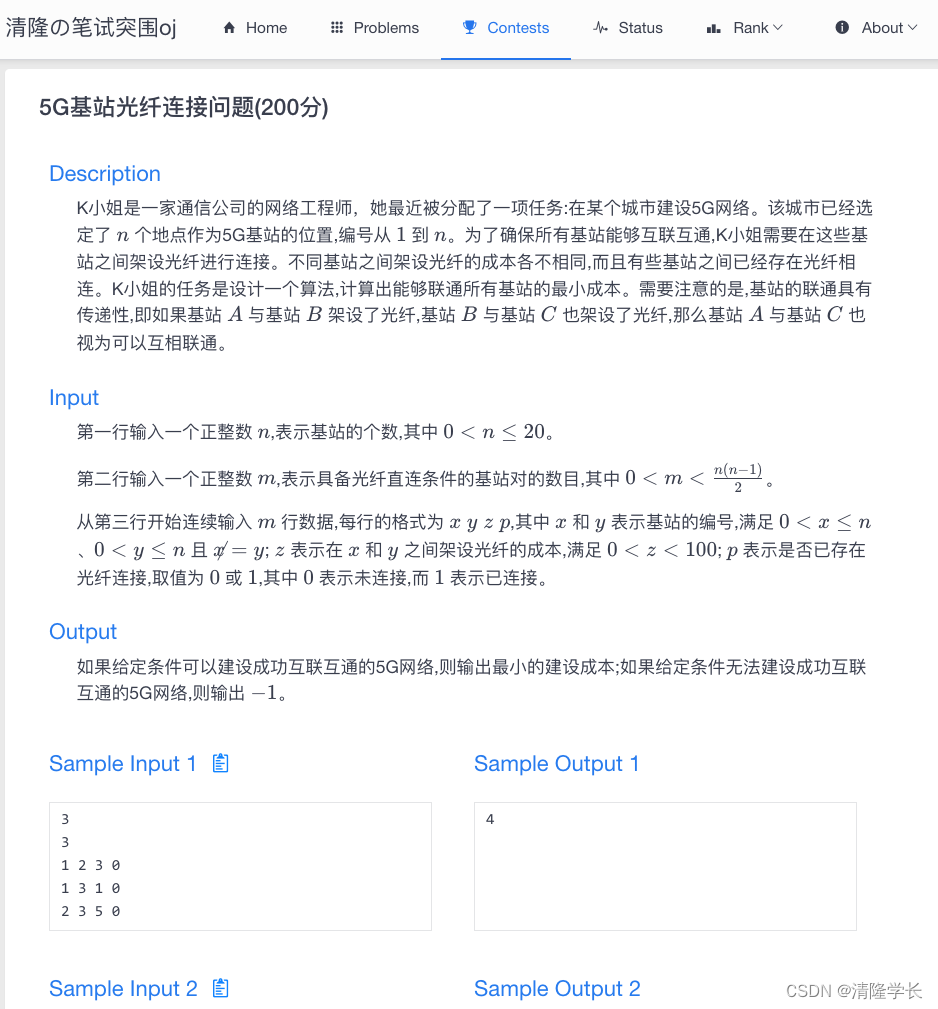
K小姐是一家通信公司的网络工程师，她最近被分配了一项任务:在某个城市建设5G网络。该城市已经选定了 $n$ 个地点作为5G基站的位置,编号从 $1$ 到 $n$。为了确保所有基站能够互联互通,K小姐需要在这些基站之间架设光纤进行连接。不同基站之间架设光纤的成本各不相同,而且有些基站之间已经存在光纤相连。K小姐的任务是设计一个算法,计算出能够联通所有基站的最小成本。需要注意的是,基站的联通具有传递性,即如果基站 $A$ 与基站 $B$ 架设了光纤,基站 $B$ 与基站 $C$ 也架设了光纤,那么基站 $A$ 与基站 $C$ 也视为可以互相联通。

输入格式

第一行输入一个正整数 $n$,表示基站的个数,其中 $0<n\le 20$。

第二行输入一个正整数 $m$,表示具备光纤直连条件的基站对的数目,其中 $0<m<\frac{n(n-1)}{2}$。

从第三行开始连续输入 $m$ 行数据,每行的格式为 $xyzp$,其中 $x$ 和 $y$ 表示基站的编号,满足 $0<x\le n$、$0<y\le n$ 且 $x\ne y$; $z$ 表示在 $x$ 和 $y$ 之间架设光纤的成本,满足 $0<z<100$; $p$ 表示是否已存在光纤连接,取值为 $0$ 或 $1$,其中 $0$ 表示未连接,而 $1$ 表示已连接。

输出格式

如果给定条件可以建设成功互联互通的5G网络,则输出最小的建设成本;如果给定条件无法建设成功互联互通的5G网络,则输出 $-1$。

样例输入

样例 1

3
3
1 2 3 0
1 3 1 0
2 3 5 0

样例 2

3
1
1 2 5 0

样例 3

3
3
1 2 3 0
1 3 1 0
2 3 5 1

样例输出

样例 1 输出

4

样例 2 输出

-1

样例 3 输出

1

样例解释

样例 1 解释

只需要在基站 $1$ 和基站 $2$ 之间,以及基站 $2$ 和基站 $3$ 之间铺设光纤,其成本为 $3+1=4$。

样例 2 解释

基站 $3$ 无法与其他基站连接,因此无法建设成功互联互通的5G网络,输出 $-1$。

样例 3 解释

基站 $2$ 和基站 $3$ 已有光纤相连,只需要在基站 $1$ 和基站 $3$ 之间铺设光纤,其成本为 $1$。

数据范围

• $0<n\le 20$
• $0<m<\frac{n(n-1)}{2}$
• $0<x,y\le n$, $x\ne y$
• $0<z<100$
• p ∈ { 0 , 1 } p \in \{0, 1\} p∈{0,1}

题解

这是一个经典的最小生成树问题,可以使用 Kruskal 算法或 Prim 算法求解。这里我们采用 Kruskal 来解决,首先将所有已经存在光纤连接的基站对进行合并,然后按照架设光纤的成本从小到大排序,依次尝试连接未连通的基站对。如果连接后不会形成环路,则将该条边加入最小生成树中。当所有基站都被连通后,最小生成树的边权之和就是最小的建设成本。

如果最终无法将所有基站连通,则输出 $-1$。

参考代码

• Python

# 并查集
class UnionFind:
    def __init__(self, n):
        self.parent = list(range(n + 1))
        self.rank = [0] * (n + 1)

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def union(self, x, y):
        px, py = self.find(x), self.find(y)
        if px == py:
            return
        if self.rank[px] < self.rank[py]:
            self.parent[px] = py
        elif self.rank[px] > self.rank[py]:
            self.parent[py] = px
        else:
            self.parent[py] = px
            self.rank[px] += 1

n = int(input())
m = int(input())
uf = UnionFind(n)
edges = []

for _ in range(m):
    x, y, w, p = map(int, input().split())
    if p == 1:
        uf.union(x, y)
    else:
        edges.append((w, x, y))

edges.sort()
cost = 0
for w, x, y in edges:
    if uf.find(x) != uf.find(y):
        uf.union(x, y)
        cost += w

if len(set(uf.find(i) for i in range(1, n + 1))) == 1:
    print(cost)
else:
    print(-1)

• Java

import java.util.*;

class UnionFind {
    int[] parent;
    int[] rank;

    public UnionFind(int n) {
        parent = new int[n + 1];
        rank = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            parent[i] = i;
        }
    }

    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    public void union(int x, int y) {
        int px = find(x);
        int py = find(y);
        if (px == py) {
            return;
        }
        if (rank[px] < rank[py]) {
            parent[px] = py;
        } else if (rank[px] > rank[py]) {
            parent[py] = px;
        } else {
            parent[py] = px;
            rank[px]++;
        }
    }
}

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        UnionFind uf = new UnionFind(n);
        List<int[]> edges = new ArrayList<>();

        for (int i = 0; i < m; i++) {
            int x = sc.nextInt();
            int y = sc.nextInt();
            int w = sc.nextInt();
            int p = sc.nextInt();
            if (p == 1) {
                uf.union(x, y);
            } else {
                edges.add(new int[]{w, x, y});
            }
        }

        edges.sort((a, b) -> a[0] - b[0]);
        int cost = 0;
        for (int[] edge : edges) {
            int w = edge[0];
            int x = edge[1];
            int y = edge[2];
            if (uf.find(x) != uf.find(y)) {
                uf.union(x, y);
                cost += w;
            }
        }

        Set<Integer> roots = new HashSet<>();
        for (int i = 1; i <= n; i++) {
            roots.add(uf.find(i));
        }

        if (roots.size() == 1) {
            System.out.println(cost);
        } else {
            System.out.println(-1);
        }
    }
}

• Cpp

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

class UnionFind {
private:
    vector<int> parent;
    vector<int> rank;

public:
    UnionFind(int n) {
        parent.resize(n + 1);
        rank.resize(n + 1, 0);
        for (int i = 0; i <= n; i++) {
            parent[i] = i;
        }
    }

    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    void merge(int x, int y) {
        int px = find(x);
        int py = find(y);
        if (px == py) {
            return;
        }
        if (rank[px] < rank[py]) {
            parent[px] = py;
        } else if (rank[px] > rank[py]) {
            parent[py] = px;
        } else {
            parent[py] = px;
            rank[px]++;
        }
    }
};

int main() {
    int n, m;
    cin >> n >> m;
    UnionFind uf(n);
    vector<vector<int>> edges;

    for (int i = 0; i < m; i++) {
        int x, y, w, p;
        cin >> x >> y >> w >> p;
        if (p == 1) {
            uf.merge(x, y);
        } else {
            edges.push_back({w, x, y});
        }
    }

    sort(edges.begin(), edges.end());
    int cost = 0;
    for (auto edge : edges) {
        int w = edge[0];
        int x = edge[1];
        int y = edge[2];
        if (uf.find(x) != uf.find(y)) {
            uf.merge(x, y);
            cost += w;
        }
    }

    bool success = true;
    int root = uf.find(1);
    for (int i = 2; i <= n; i++) {
        if (uf.find(i) != root) {
            success = false;
            break;
        }
    }

    if (success) {
        cout << cost << endl;
    } else {
        cout << -1 << endl;
    }

    return 0;
}