算法基础精选题单 动态规划（dp）（区间dp）（个人题解）

news2024/10/6 1:24:49

目录

前言：

正文：

  题单：【237题】算法基础精选题单_ACM竞赛_ACM/CSP/ICPC/CCPC/比赛经验/题解/资讯_牛客竞赛OJ_牛客网 (nowcoder.com)

NC50493 石子合并：

NC50500 凸多边形的划分：

NC235246 田忌赛马：

NC13230 合并回文子串:

NC16645 [NOIP2007]矩阵取数游戏：

NC207781 迁徙过程中的河流：

后记：

前言：

  这些dp对我来说就没那么简单了，但写过这些题目之后我确实对区间dp有了一个简单的认识，区间dp一般都是二维的，由第一维表示左端点，第二维表示右端点，且状态一般由区间长度小的转移而来，所以我们写dp的转移时第一层循环由len来从小枚举区间长度，第二层循环枚举区间的左端点l，右端点就可以直接表示为l+len-1（也可先枚举右端点，再从右端点往左枚举左端点），初始化和状态转移方程就得根据相应题目来了，在写这写题目时我也学会了其他的一些技巧，比如环形数组的题该如何写以及__int128的用法（用来处理一些暴long long）的情况。

正文：

  题单：【237题】算法基础精选题单_ACM竞赛_ACM/CSP/ICPC/CCPC/比赛经验/题解/资讯_牛客竞赛OJ_牛客网 (nowcoder.com)

NC50493 石子合并：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[410],dp1[410][410],dp2[410][410],pre[410];
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		a[i+n]=a[i];
	}
	for(int i=1;i<=2*n;i++){
		pre[i]=pre[i-1]+a[i];
	}
	memset(dp1,127,sizeof(dp1));
	memset(dp2,0,sizeof(dp2));
	for(int j=1;j<=2*n;j++){
		for(int i=j;i>=1;i--){
			if(i==j)dp1[i][j]=dp2[i][j]=0;
			for(int k=i;k<j;k++){
				dp1[i][j]=min(dp1[i][k]+dp1[k+1][j]+pre[j]-pre[i-1],dp1[i][j]);
				dp2[i][j]=max(dp2[i][k]+dp2[k+1][j]+pre[j]-pre[i-1],dp2[i][j]);
			}
			//cout<<i<<" "<<j<<" "<<dp1[i][j]<<endl;
		}
	}
	ll ansn=0x3f3f3f3f,ansm=0;
	for(int i=1;i<=n;i++){
		ansn=min(ansn,dp1[i][i+n-1]);
		ansm=max(ansm,dp2[i][i+n-1]);
	}
	cout<<ansn<<endl<<ansm<<endl;
	return 0;
}

这题原型是比较经典的模板题，这题在原题上做了些修改，一是要求最小和最大的值，二是这是个环形的数组；对于一我们处理两个不同初值的dp数组， 分别求min,max，对于二我们则将数组扩大到2n，a[n+i]=a[i]，这样枚举就能表示环形数组的所有情况，不过最后我们求答案时也要枚举所有长度为n的区间dp值。

dp的初始状态为 dp[i][j]=0（i==j ）

dp的状态转移方程我们可以知道为:

dp[i][j]=dp[i,k]+dp[k+1,j]+pre[j]-pre[i-1]

其中dp[i][j]表示将从石头i到石头j合并的得分（dp1为最小，dp2为最大）（同理dp[i][k]及dp[j]），pre[j]-pre[i-1]为此次合并的得分，由前缀和表示。

由此得结果。

NC50500 凸多边形的划分：

#include<bits/stdc++.h>
using namespace std;
__int128 read(){
	//直接在函数里面实现读字符串操作更简洁
	__int128 res=0;//初始结果赋值0
	char scan[1005];
	scanf("%s",scan);
	for(int i=0;i<strlen(scan);i++)
		res*=10,res+=scan[i]-'0';//实现进位
	return res;//返回__int128类型
}
void print(__int128 num){//递归调用，实现从高位向低位输出
	if(num>9) print(num/10);
	putchar(num%10+'0');
}
__int128 a[55],dp[55][55];
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		a[i]=read();
	}
	for(int l=3;l<=n;l++){
		for(int i=1;i+l-1<=n;i++){
			int j=i+l-1;
			dp[i][j]=1e30;
			for(int k=i+1;k<j;k++){
				dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]+a[i]*a[k]*a[j]);
			}
		}
	}
	print(dp[1][n]);
	return 0;
}

这题像是能量项链的变式。状态转移方程为下：

dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]+a[i]*a[k]*a[j])

画个图大家自己体会下（可能不是很形象）：

其中dp[i][j]表示将i到j点这个多边形分割后权值和的最小值(i,j在这里是一个表示首，一个表示尾)，

a[i]*a[k]*a[j]为这个三角形的权值。

由于要求最小值，所以初始化为最大数，在加上数据会暴long long ，所以这里就要用到__int128了，他可以表示-2^127~2^127大小的数，但不能直接输入输出，必须采用我代码中那样的自定义函数。

NC235246 田忌赛马：

#include<bits/stdc++.h>
using namespace std;
const int N=2005;
int a[N],b[N],g[N][N],dp[N][N];
bool cmp(int n1,int n2){
	return n1>n2;
}
int main(){
	int n,ans;
	cin>>n;
	for(int i=1;i<=n;++i)cin>>a[i];
	for(int i=1;i<=n;++i)cin>>b[i];
	sort(a+1,a+n+1,cmp),sort(b+1,b+n+1,cmp);
	for(int i=1;i<=n;++i)
		for(int j=1;j<=n;++j){
			if(a[i]>b[j]) g[i][j]=200;
			else if(a[i]==b[j]) g[i][j]=0;
			else g[i][j]=-200;
		}
	for(int i=1;i<=n;++i){
		dp[i][0]=dp[i-1][0]+g[n-i+1][i];
		dp[i][i]=dp[i-1][i-1]+g[i][i];
		for(int j=1;j<i;++j) dp[i][j]=max(dp[i-1][j]+g[n-i+j+1][i],dp[i-1][j-1]+g[j][i]);
	}
	ans=dp[n][1];
	for(int i=2;i<=n;++i)ans=max(ans,dp[n][i]);
	cout<<ans<<endl;
	return 0;
}

首先给国王和田忌的马从小到大排序

接下来是贪心策略：

  1. 首先比最快的马，如果能赢就直接赢。
  2. 如果赢不了，就比国王和田忌最慢的马，能赢就赢。
  3. 如果最慢的马也赢不了，就用最慢的马去对国王最快的马。

设dp[i][j]表示齐王按从强到弱的顺序出马和田忌进行了i场比赛之后，从""头""取了j匹较强的马，从""尾""取了i-j匹较弱的马，所能获得的最大盈利。

其中g[i][j]表示田忌的马和齐王的马分别按照由强到弱的顺序排序之后，田忌的第 i 匹马和齐王的第 j 匹马赛跑所能取得的盈利，胜为 200 ，负为 −200 ，平为 0。

得状态转移方程为：

dp[i][j]=max(dp[i-1][j]+g[n-i+j+1][i],dp[i-1][j-1]+g[j][i]

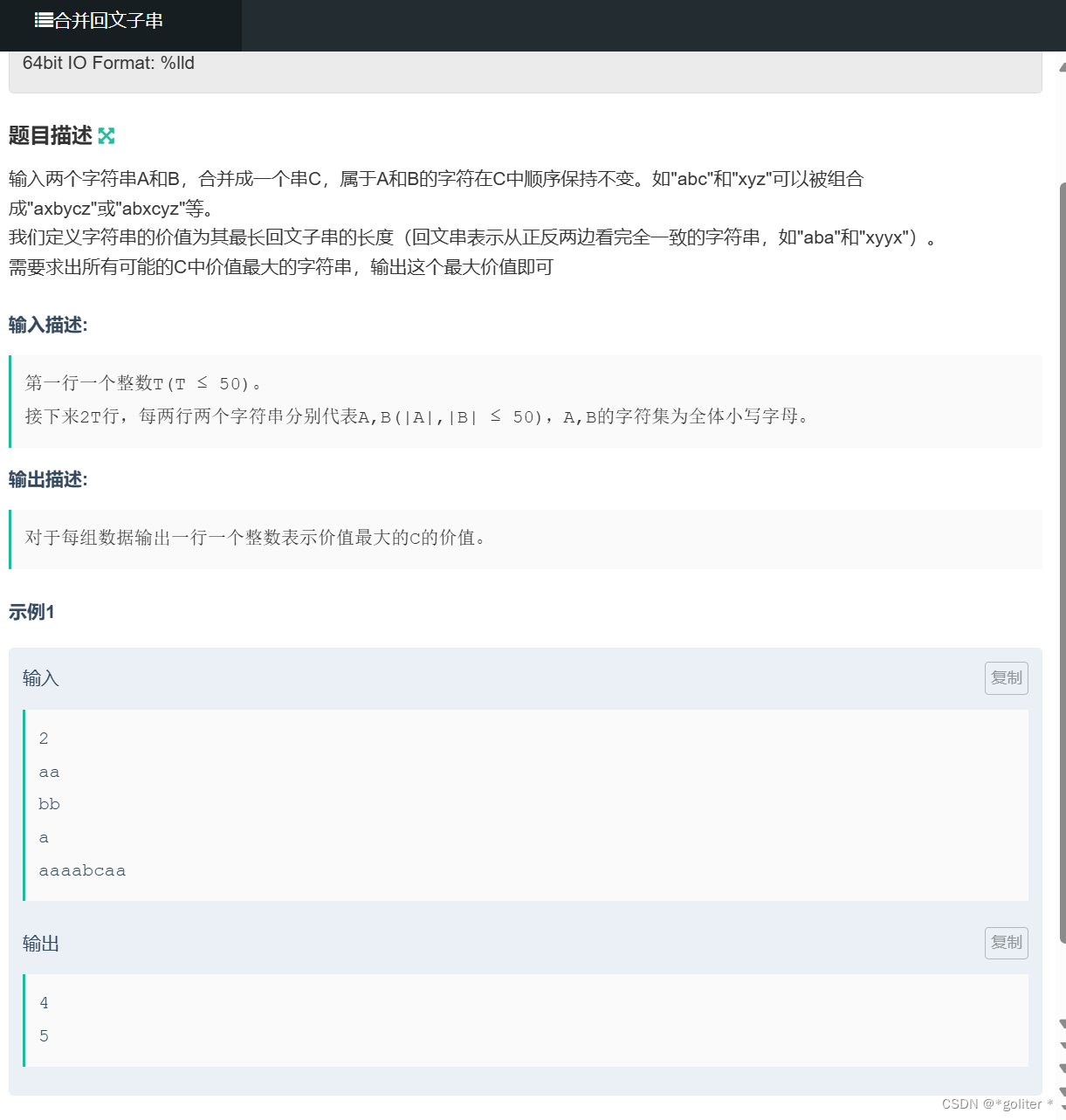
NC13230 合并回文子串:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e6+5;
char a[N],b[N];
ll dp[55][55][55][55];
int main(){
	int t;
	cin>>t;
	while(t--){
		memset(dp,0,sizeof(dp));
		int ans=0;
		scanf("%s",a+1);
		scanf("%s",b+1);
		int sa=strlen(a+1),sb=strlen(b+1);
		for(int x=0;x<=sa;x++){
			for(int y=0;y<=sb;y++){
				for(int i=1,j=x;j<=sa;i++,j++){
					for(int k=1,l=y;l<=sb;k++,l++){
						if(x+y<=1) dp[i][j][k][l]=1;
						else{
							if(a[i]==a[j]) dp[i][j][k][l]|=dp[i+1][j-1][k][l];
                            if(b[k]==b[l]) dp[i][j][k][l]|=dp[i][j][k+1][l-1];
                            if(a[i]==b[l]) dp[i][j][k][l]|=dp[i+1][j][k][l-1];
                            if(b[k]==a[j]) dp[i][j][k][l]|=dp[i][j-1][k+1][l];
						}
						if(dp[i][j][k][l])ans=max(ans,x+y);
					}
				}
			}
		}
		cout<<ans<<endl;
	}
	return 0;
}

初始状态只有一个字母的状态一定是回文。

假设A[i] ~ A[j]与B[k] ~ B[l]构成了一个回文串(这里设dp[i][j][k][l])，则他能转移到的区间有
1：a[i-1]==a[j+1]时 dp[i-1][j+1][k][l]
2：a[i-1]==b[l+1]时 dp[i-1][j][k][l+1]
3：b[k-1]==a[j+1]时 dp[i][j+1][k-1][l]
4：b[k-1]==b[l+1]时 dp[i][j][k-1][l+1]
那么对应的转移方程就为

if(a[i]==a[j]) dp[i][j][k][l]|=dp[i+1][j-1][k][l];

if(a[i]==b[l]) dp[i][j][k][l]|=dp[i+1][j][k][l-1];

if(b[k]==b[l]) dp[i][j][k][l]|=dp[i][j][k+1][l-1];

if(b[k]==a[j]) dp[i][j][k][l]|=dp[i][j-1][k+1][l];

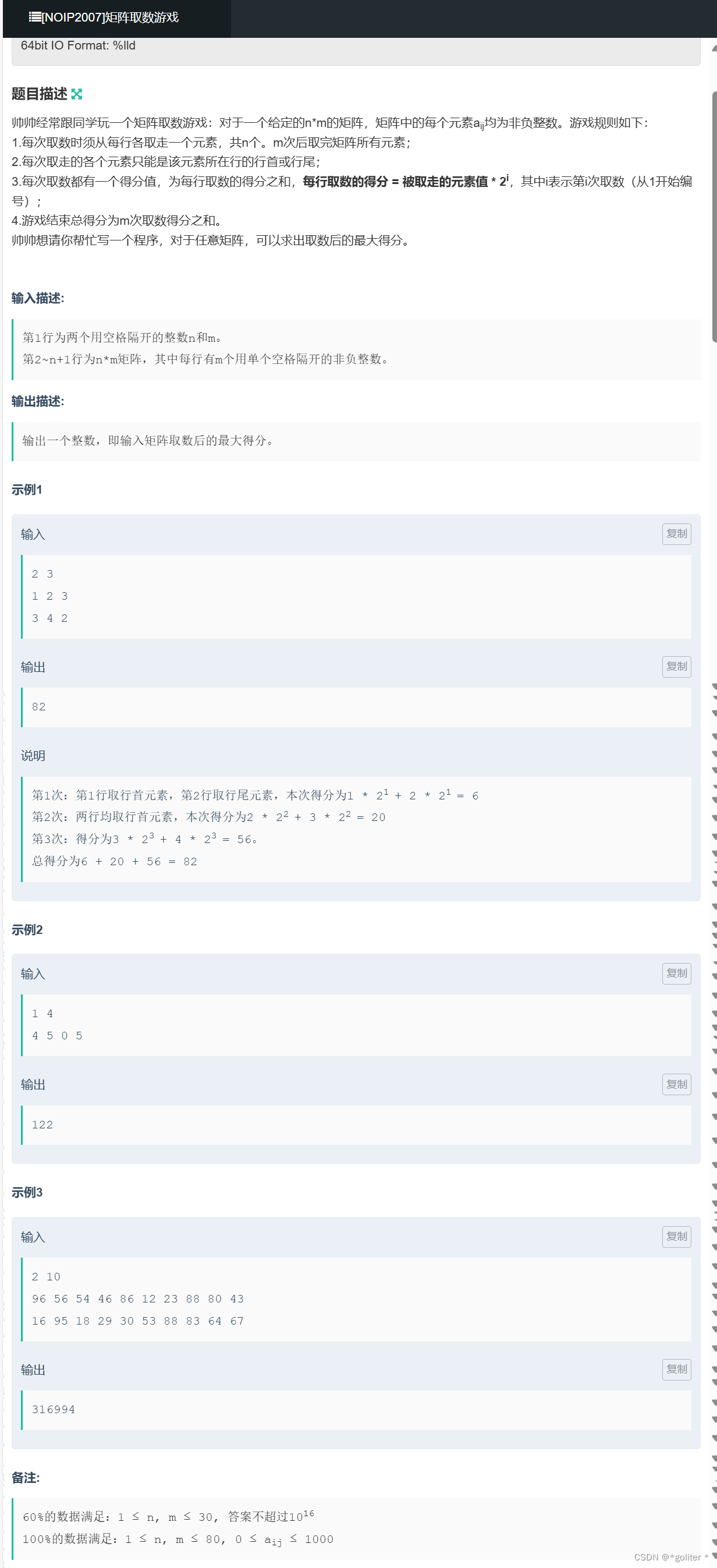
NC16645 [NOIP2007]矩阵取数游戏：

#include<bits/stdc++.h>
using namespace std;
__int128 read(){
    //直接在函数里面实现读字符串操作更简洁
    __int128 res=0;//初始结果赋值0
    char scan[1005];
    scanf("%s",scan);
    for(int i=0;i<strlen(scan);i++)
        res*=10,res+=scan[i]-'0';//实现进位
    return res;//返回__int128类型
}
void print(__int128 num){//递归调用，实现从高位向低位输出
    if(num>9) print(num/10);
    putchar(num%10+'0');
}
typedef long long ll;
__int128 pow2(__int128 a,__int128 b){
	__int128 res=1;
	while(b){
		if(b&1)res*=a;
		a*=a,b/=2;
	}
	return res;
}
__int128 a[100][100];
__int128 dp[100][100][100];
int main(){
	ll n,m;
	__int128 ans=0;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			a[i][j]=read();
		}
	}
	for(int k=1;k<=n;k++){
		for(int len=1;len<=m;len++){
			for(int i=1;i<=m,i+len-1<=m;i++){
				int j=i+len-1;
				if(i==j)dp[i][j][k]=a[k][i]*pow2(2,m-len+1);
				else dp[i][j][k]=max(dp[i+1][j][k]+a[k][i]*pow2(2,m-len+1),dp[i][j-1][k]+a[k][j]*pow2(2,m-len+1));
				//cout<<i<<" "<<j<<" "<<k<<" "<<dp[i][j][k]<<endl;
			}
		}
		//cout<<dp[1][m][k]<<endl;
		ans+=dp[1][m][k];
	}
	print(ans);
	return 0;
}

（自己独立思考写出来的，很有成就感）

因为每次只能取行首或者行尾，所以每行取得顺序都是独立的，由此可以从求最大的得分和转换成求每行的最大得分和。然后用区间dp计算每一行，状态转移方程为：

dp[i][j][k]=max(dp[i+1][j][k]+a[k][i]*pow2(2,m-len+1),dp[i][j-1][k]+a[k][j]*pow2(2,m-len+1))

k表示第几行.i,j表示区间，a[k][i]*pow2(2,m-len+1)表示取该数的得分，根据len来判断这次为第几次取数。

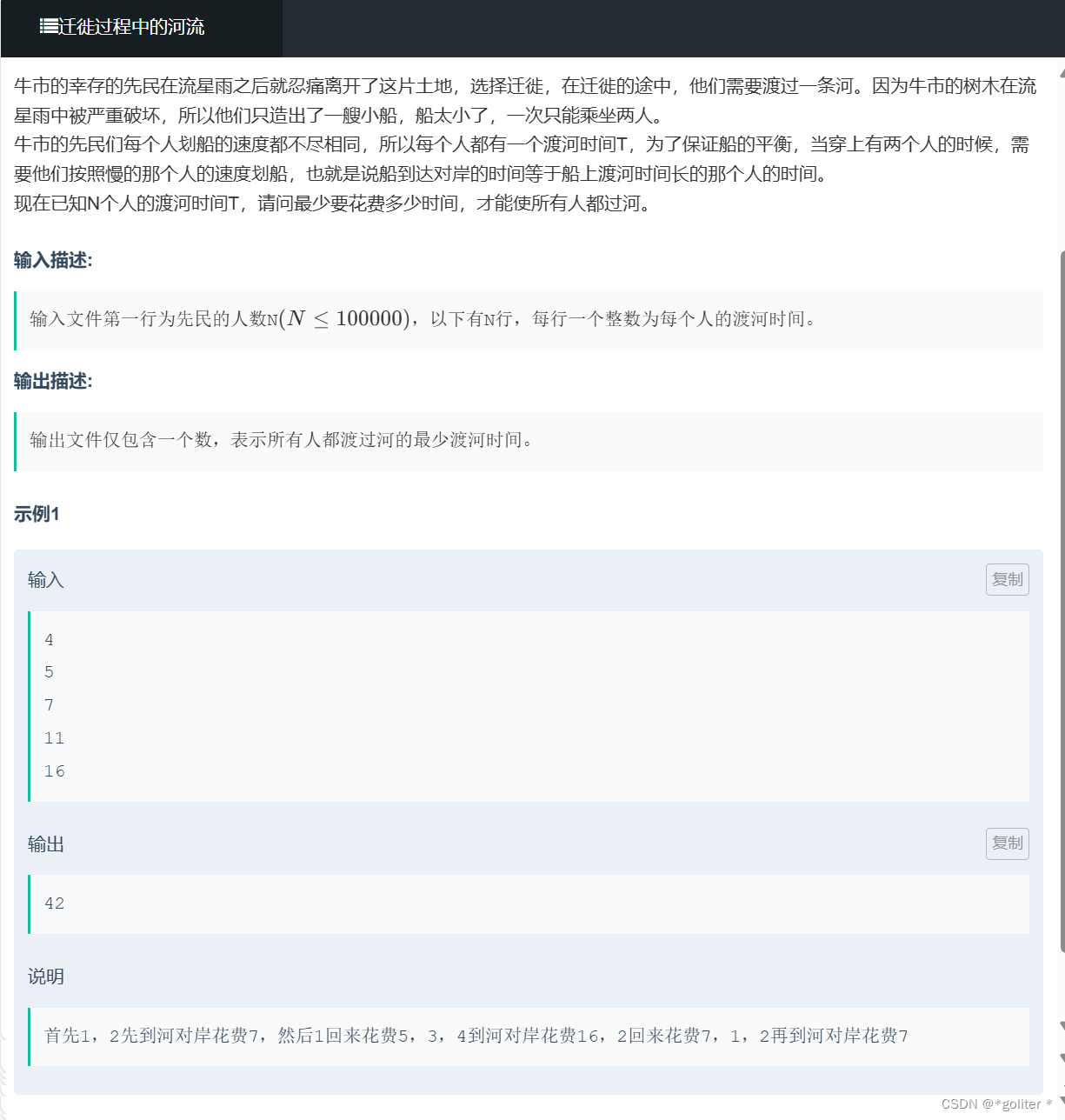
NC207781 迁徙过程中的河流：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[100005],dp[100005];
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	sort(a+1,a+n+1);
	dp[1]=a[1];dp[2]=a[2];
	for(int i=3;i<=n;i++){
		dp[i]=min(dp[i-1]+a[1]+a[i],dp[i-2]+a[1]+2*a[2]+a[i]);
	}
	cout<<dp[n];
	return 0;
}

说实话这题更像是线性dp，从题目中规律可以看出来在某个人要过河的时候要么是最快的那个人来接他，要么是还剩下两个让最快的把船开回来然后让这两个过去，之后让第二快的把船开过来，全部过去。这两个在题目中的样例里面都有体现。转移方程为：

dp[i]=min(dp[i-1]+a[1]+a[i],dp[i-2]+a[1]+2*a[2]+a[i])

后记：

  题对我确实很难，不过我也还算收获满满，写博客过程中也相当于是把写题过程在梳理了一遍，希望这篇博客不只能帮助到我自己吧。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1847122.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

数据库浅识及MySQL的二进制安装

数据库浅识及MySQL的二进制安装

数据库基础概念与MySQL二进制安装与初始化 使用数据库的必要性 数据库可以结构化储存大量数据信息&#xff0c;方便用户进行有效的检索访问 有效的保持数据信息的一致性&#xff0c;完整性&#xff0c;降低数据冗余 可以满足应用的共享和安全方面的要求 数据库基本概念 数据…
阅读更多...
[dataworks]从mysql导入数据、将结果导入到mysql、处理写错表名问题、创建依赖任务

[dataworks]从mysql导入数据、将结果导入到mysql、处理写错表名问题、创建依赖任务

一、从mysql导入数据 在ods的数据集成下点新建-->离线同步 1、起名imp_t_ods_uc_cst_terminal_dtl_df 前缀imp是import的缩写 t代表trade即MySQL的交易库(trade)的简写 ods即导入到ods层 uc_cst_terminal_dt为MySQL对应的表名 df为日全量导入&#xff08;di为日增量导…
阅读更多...
真实还原汽车引擎声浪——WT2003Hx语音芯片方案

真实还原汽车引擎声浪——WT2003Hx语音芯片方案

PART.01 产品市场 WT2003Hx是一款高性能的MP3音频解码芯片&#xff0c;具有成本效益、低功耗和高可靠性等特点&#xff0c;适用于多种场景&#xff0c;包括但不限于汽车娱乐系统、玩具、教育设备以及专业音响设备等。在模拟汽车引擎声的应用中&#xff0c;这一芯片的特性被特…
阅读更多...
推荐一个十分好用的AI工具

推荐一个十分好用的AI工具

推荐一个很好用的ai工具 链接在最下面 **介绍** ChatGPT 是由OpenAI开发的先进语言模型&#xff0c;旨在通过自然而流畅的对话方式与用户交互。无论是解决问题、提供建议&#xff0c;还是进行创意灵感的激发&#xff0c;ChatGPT都能为用户提供帮助。 **特点与优势** 1. **广泛…
阅读更多...
JMeter的基本使用与性能测试，完整入门篇保姆式教程

JMeter的基本使用与性能测试，完整入门篇保姆式教程

Jmeter 的简介 JMeter是一个纯Java编写的开源软件&#xff0c;主要用于进行性能测试和功能测试。它支持测试的应用/服务/协议包括Web (HTTP, HTTPS)、SOAP/REST Webservices、FTP、Database via JDBC等。我们最常使用的是HTTP和HTTPS协议。 Jmeter主要组件 线程组&#xff08…
阅读更多...
【C++进阶学习】第三弹——菱形继承和虚拟继承——菱形继承的二义性和数据冗余问题

【C++进阶学习】第三弹——菱形继承和虚拟继承——菱形继承的二义性和数据冗余问题

继承&#xff08;上&#xff09;&#xff1a;【C进阶学习】第一弹——继承&#xff08;上&#xff09;——探索代码复用的乐趣-CSDN博客 继承&#xff08;下&#xff09;&#xff1a;【C进阶学习】第二弹——继承&#xff08;下&#xff09;——挖掘继承深处的奥秘-CSDN博客 …
阅读更多...
雷池社区版自动SSL

雷池社区版自动SSL

正常安装雷池&#xff0c;并配置站点&#xff0c;暂时不配置ssl 不使用雷池自带的证书申请。 安装&#xff08;acme.sh&#xff09;&#xff0c;使用域名验证方式生成证书 先安装git yum install git 或者 apt-get install git 安装完成后使用 git clone https://gitee.com/n…
阅读更多...
(项目实战)RocketMQ5.0延迟消息在聚合支付系统中的应用

(项目实战)RocketMQ5.0延迟消息在聚合支付系统中的应用

1 基于业务场景掌握RocketMQ5.0 本篇文章主要结合聚合支付系统中的业务场景来落地RocketMQ中间件的应用&#xff0c;聚合支付系统主要在支付系统超时订单和商户支付结果异步通知场景中会使用到RocketMQ消息中间件。本文使用到了RocketMQ中的延迟消息知识点&#xff0c;RocketM…
阅读更多...
SD-WAN为什么适合小企业

SD-WAN为什么适合小企业

SD-WAN&#xff08;软件定义广域网&#xff09;是一种革新性的网络技术&#xff0c;通过软件智能管理&#xff0c;实现灵活和高效的网络连接。在数字化转型浪潮中&#xff0c;企业对网络稳定性和性能的要求不断提升&#xff0c;SD-WAN因此受到了广泛关注。对于资源有限的小型企…
阅读更多...
laravel中如何向字段标签添加工具提示

laravel中如何向字段标签添加工具提示

首先&#xff0c;您可以使用 轻松自定义字段标签->label()。我相信您知道这一点。但您知道吗……标签输出未转义&#xff1f;这意味着您也可以在标签中包含 HTML。 为了尽快实现上述目标&#xff0c;我只是采取了一个快速而粗糙的解决方案&#xff1a; CRUD::field(nickna…
阅读更多...
扭转引伸计技术资料YYJ-10 6-N

扭转引伸计技术资料YYJ-10 6-N

一、 工作原理 利用专门设计的扭转引伸计夹持系统&#xff0c;可靠地装夹在试样上&#xff0c;采用应变片夹式引伸计进行机械量与电信号的转换&#xff0c;使之完成扭转应变的自动测试。 二、技术指标 1、扭转引伸计的标距&#xff1a;该装置分别配置50mm、100mm标距联接延伸横…
阅读更多...
一键制作，打造高质量的数字刊物

一键制作，打造高质量的数字刊物

随着数字化时代的到来&#xff0c;数字刊物已经成为信息传播的重要载体。它以便捷、环保、互动性强等特点&#xff0c;受到了越来越多人的青睐。然而&#xff0c;如何快速、高效地制作出高质量的数字刊物&#xff0c;成为许多创作者面临的难题。今天&#xff0c;教大家一个制作…
阅读更多...
浅析MySQL-基础02

浅析MySQL-基础02

目录 MySQL一行记录是怎么存储的&#xff1f; MySQL的数据存放在哪&#xff1f; 表空间文件的结构是怎么样的&#xff1f; InnoDB行格式有哪些&#xff1f; Compact行格式是啥样的&#xff1f; 记录的额外信息 1、变长字段长度列表 2、NULL值列表 3、记录头信息 记录…
阅读更多...
LeetCode题练习与总结：克隆图--133

LeetCode题练习与总结：克隆图--133

一、题目描述 给你无向 连通 图中一个节点的引用&#xff0c;请你返回该图的 深拷贝&#xff08;克隆&#xff09;。 图中的每个节点都包含它的值 val&#xff08;int&#xff09; 和其邻居的列表&#xff08;list[Node]&#xff09;。 class Node {public int val;public L…
阅读更多...
【EndNote】EndNote进行文献管理可能遇到的问题和解决方案

【EndNote】EndNote进行文献管理可能遇到的问题和解决方案

一、安装GB/T7714-2015(numberic)文献style windows&#xff1a;https://blog.csdn.net/qq_36235935/article/details/115629694 mac os&#xff1a;Mac版Endnote 20导入中文参考格式Chinese Std GBT7714 (numeric)-CSDN博客 安装完之后需要调整Author Name格式&#xff1a;…
阅读更多...
Linux内核学习——linux内核体系结构（1）

Linux内核学习——linux内核体系结构（1）

1 Linux内核模式 学习的是Linux 0.11内核&#xff0c;采用的是单内核模式。单内核模式的主要优点是内核代码结构紧凑、执行速度快&#xff0c;但是层次结构性不强。 操作系统如何提供的服务流程&#xff1f; 应用主程序使用指定的参数值执行系统调用指令(int x80)&#xff0…
阅读更多...
用进程和线程完成TCP进行通信操作及广播和组播的通信

用进程和线程完成TCP进行通信操作及广播和组播的通信

进程 代码 #include <stdio.h>#include <sys/types.h>#include <sys/socket.h>#include <netinet/in.h>#include <arpa/inet.h>#include <string.h>#include <unistd.h>#include <stdlib.h>#include <signal.h>#includ…
阅读更多...
如何使用idea连接Oracle数据库？

如何使用idea连接Oracle数据库？

idea版本&#xff1a;2021.3.3 Oracle版本&#xff1a;10.2.0.1.0&#xff08;在虚拟机Windows sever 2003 远程连接数据库&#xff09; 数据库管理系统&#xff1a;PLSQL Developer 在idea里面找到database&#xff0c;在idea侧面 选择左上角加号&#xff0c;新建&#xff…
阅读更多...
消息队列kafka中间件详解：案例解析(第10天)

消息队列kafka中间件详解：案例解析(第10天)

系列文章目录 1- 消息队列&#xff08;熟悉&#xff09;2- Kafka的基本介绍&#xff08;掌握架构&#xff0c;其他了解&#xff09;3- Kafka的相关使用&#xff08;掌握kafka常用shell命令&#xff09;4- Kafka的Python API的操作&#xff08;熟悉&#xff09; 文章目录 系列文…
阅读更多...
0.15元1.5Mhz-1.3A同步整流BUCK降压DCDC芯片MT3410(MT3410LB)

0.15元1.5Mhz-1.3A同步整流BUCK降压DCDC芯片MT3410(MT3410LB)

前言 国产同步整流DCDC&#xff0c;参考价格约0.15元。 特征 高效率&#xff1a;高达 96% 1.5MHz恒定频率操作 1.3A 输出电流 无需肖特基二极管 2.3V至7V输入电压范围 输出电压低至 0.6V PFM 模式可在轻负载下实现高效率 压差操作中的100%占空比 低静态电流&#xff1a;35μ…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023