向量相似性搜索彻底改变了搜索领域。它允许我们高效地检索从GIF到文章等各种媒体,即使在处理十亿级别数据集时,也能在亚秒级时间内提供令人印象深刻的准确性。
然而,这种灵活性也带来了一个问题:如何知道哪种索引大小最适合我们的用例?应选择哪种索引?是否只需要一个索引?本文将探讨几种关键索引(Flat、LSH、HNSW和IVF)的优缺点,并指导如何选择适合用例的索引,以及每个索引中参数的影响。
索引在搜索中的应用
在我们深入探讨不同类型的索引之前,让我们先了解为什么它们如此重要,以及我们如何利用它们进行高效的相似性搜索。
相似性搜索的价值
相似性搜索可以用来快速比较数据。给定一个查询(可能是任何格式——文本、音频、视频、GIF等,您能想到的都有),可以使用相似性搜索返回相关结果。
相似性搜索的核心在于快速比较数据,以便返回相关结果。这对于各行各业的公司和应用至关重要,如基因数据库的基因识别、数据的去重,以及每天处理数十亿搜索结果。
高效搜索的索引
在向量相似性搜索中,索引用于存储数据的向量表示,并通过统计方法或机器学习构建编码原始数据有用信息的向量。将“有意义”的向量存储在索引中,以便进行智能相似性搜索。
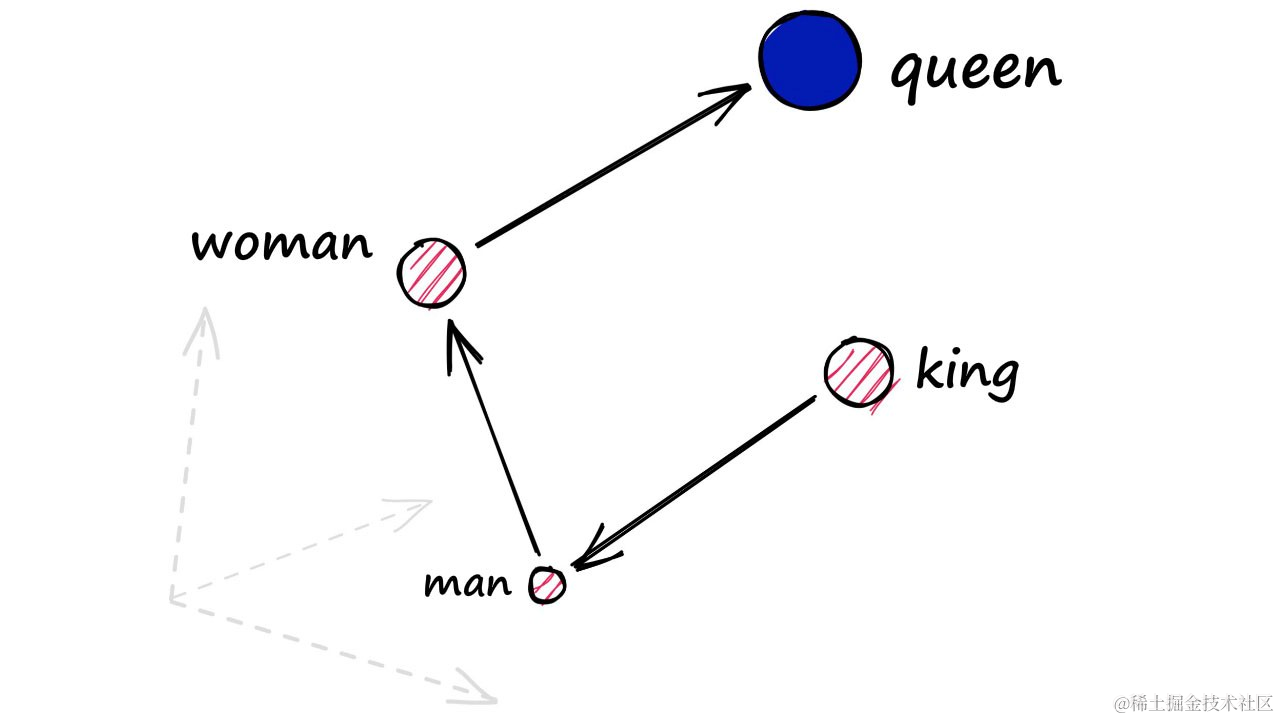
使用密集编码的向量,可以展示man-King语义关系对woman来说是equivalent的Queen。
将“有意义”的向量存储在索引中,可以实现智能的相似性搜索。这种搜索依赖于索引中的向量表示,这些向量通常通过统计方法或机器学习算法从原始数据中提取。Faiss(Facebook AI相似性搜索)是一个流行的索引解决方案,它允许我们存储向量并在Faiss索引中使用“查询”向量进行搜索。通过比较查询向量与索引中的其他向量,可以找到最接近的匹配,通常使用欧几里得(L2)或内积(IP)度量。
了解了相似性搜索的基本概念后,接下来将探讨如何选择正确的Faiss索引,以及如何调整索引参数以优化搜索性能。
Faiss索引的选择
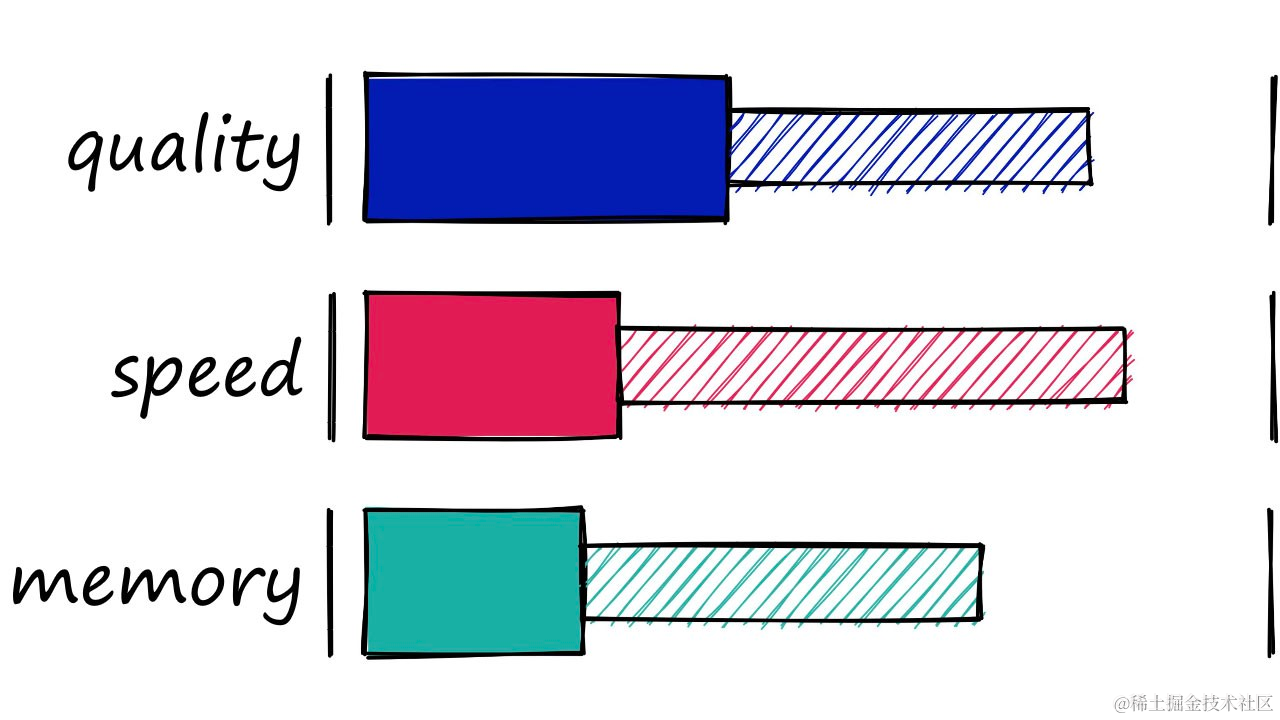
Faiss 提供了多种索引类型,这些类型可以相互组合,以构建多层级的索引结构。在选择索引时,需考虑不同的因素,如搜索速度、质量或索引内存的需求。具体使用哪种索引,应基于我们的用例,并考虑数据集的大小、搜索的频率以及对于搜索质量与速度的权衡。

Flat索引
Flat 索引以牺牲搜索速度为代价,提供了完美的搜索质量。这种索引的内存利用率是合理的。Flat 索引是最简单的一种,它不修改输入的向量,因此产生了最准确的结果。然而,这种完美的搜索质量需要较长时间来完成。在 Flat 索引中,查询向量与索引中的每个其他全尺寸向量进行比较,以计算它们的距离。
Flat和准确率
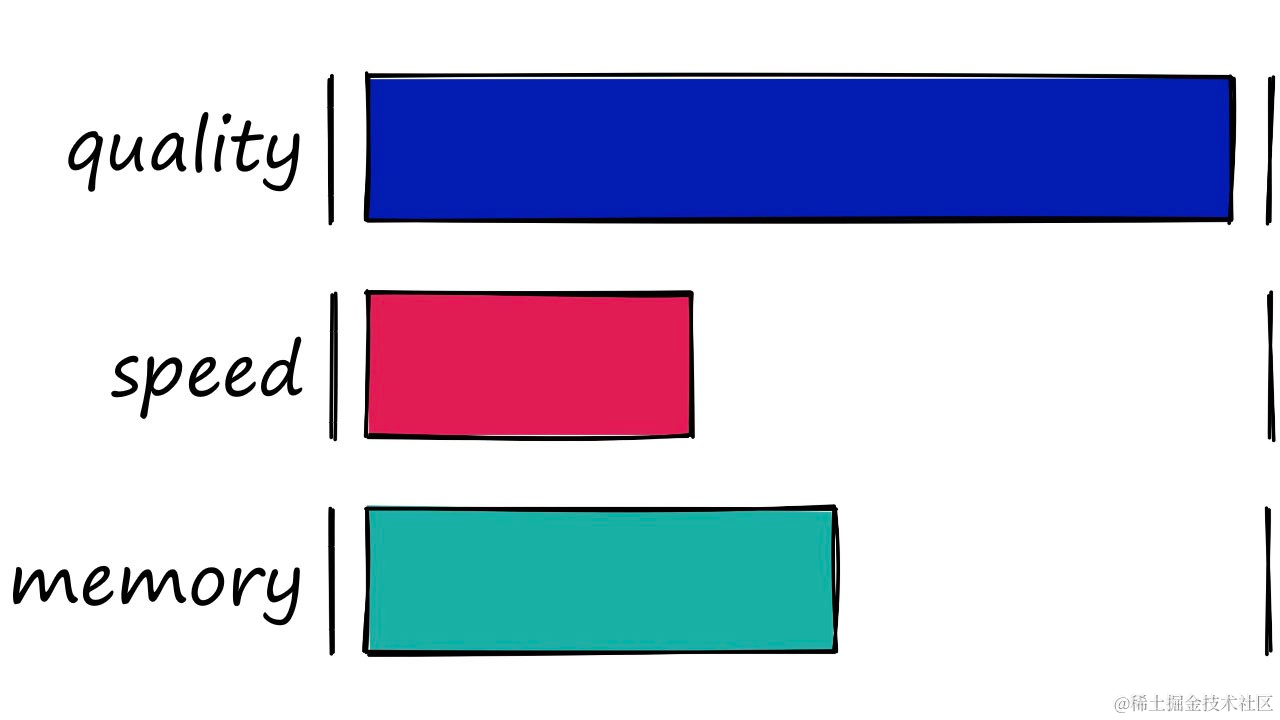
Flat索引在完美的搜索质量上付出了搜索速度慢的代价。Flat索引的内存利用率是合理的。
Flat 索引是最简单且直接的索引类型,它不对输入的向量进行任何修改,因此提供了最准确的结果。这种索引在搜索质量上追求完美,但代价是较慢的搜索速度。在 Flat 索引中,查询向量与索引中的每个其他全尺寸向量进行比较,以计算它们的距离。一旦完成了所有距离的计算,就可以返回与查询向量最接近的 k 个向量。
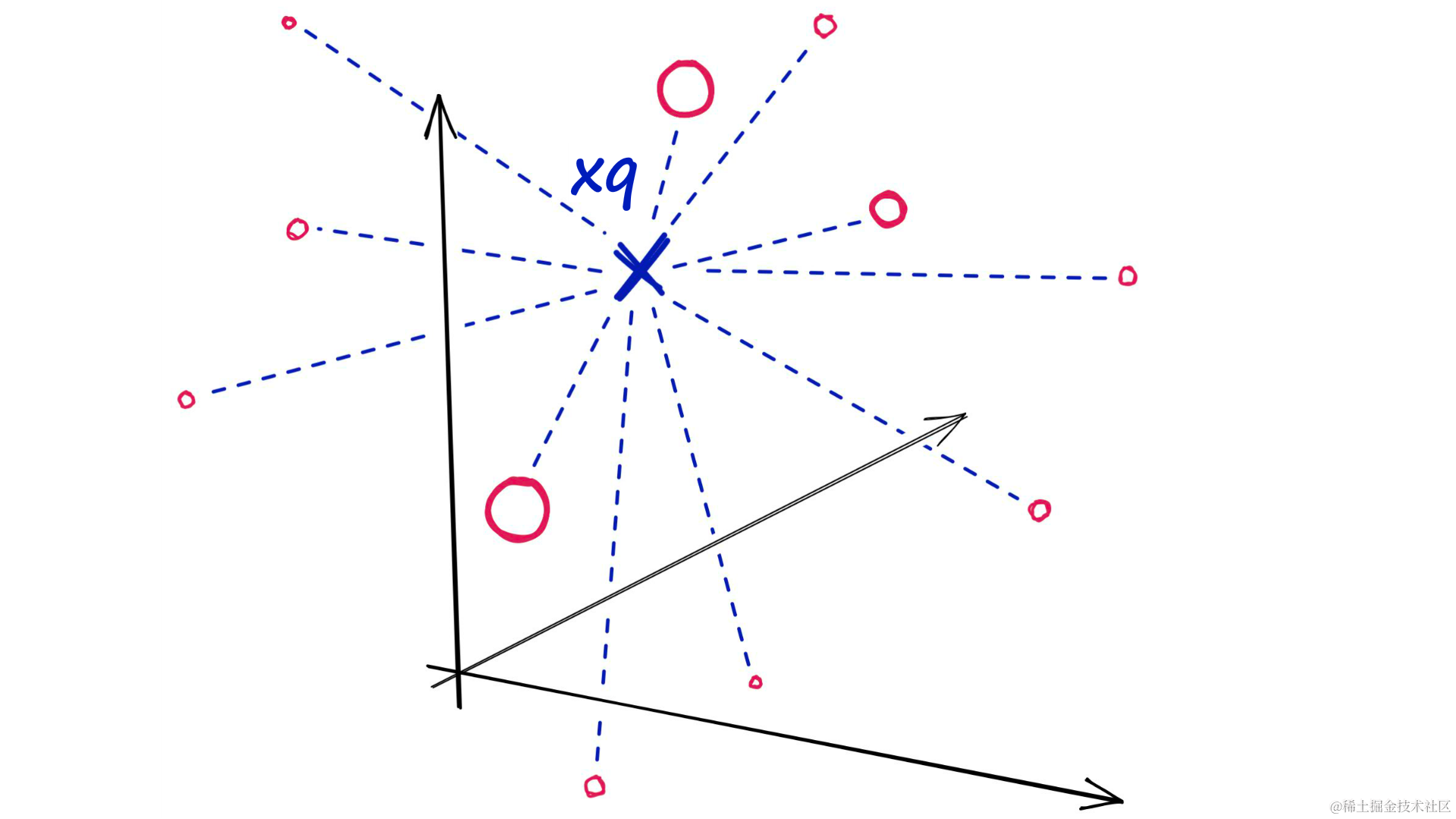
计算所有距离后,返回 k 个最接近的向量。
何时使用Flat 索引
Flat 索引适合于搜索质量是首要考虑因素,而对搜索速度要求不高的情况。特别适用于小型数据集,尤其是在使用高性能硬件时。

在 M1 芯片上使用 faiss-cpu 进行欧几里得(L2)和内积(IP)平面索引搜索的时间表明,IndexFlatIP 比 IndexFlatL2 略快(100维度向量)
上面的图表展示了M1芯片上的Faiss CPU速度。当与Linux上的CUDA兼容GPU配对时,Faiss被优化以在GPU上运行,速度显著提高,从而显著提高搜索时间。
简而言之,当以下情况时,使用平面索引:
- 搜索质量是一个非常重要的优先事项。
- 搜索时间不重要或者当使用小索引(<10K)时。
实现 Flat 索引
要初始化一个 Flat 索引需要准备数据和 Faiss,选择合适的平面索引,如 IndexFlatL2 或 IndexFlatIP。以下是如何使用 Sift1M 数据集的示例代码:
import shutil
import urllib.request as request
from contextlib import closing
# 下载 Sift1M 数据集
with closing(request.urlopen('ftp://ftp.irisa.fr/local/texmex/corpus/sift.tar.gz')) as r:
with open('sift.tar.gz', 'wb') as f:
shutil.copyfileobj(r, f)
import tarfile
# 解压数据集
tar = tarfile.open('sift.tar.gz', "r:gz")
tar.extractall()
import numpy as np
# 读取 fvecs 文件
def read_fvecs(fp):
a = np.fromfile(fp, dtype='int32')
d = a[0]
return a.reshape(-1, d + 1)[:, 1:].copy().view('float32')
xb = read_fvecs('sift_base.fvecs') # 1M samples
xq = read_fvecs('./sift/sift_query.fvecs')
xq = xq[0].reshape(1, xq.shape[1])
xq.shape # (1, 128)
xb.shape # (1000000, 128)
# 初始化索引
d = 128 # 数据维度
k = 10 # 最近邻数量
index = faiss.IndexFlatIP(d)
index.add(xb)
D, I = index.search(xq, k)
平衡搜索时间
平面索引的准确性极高,但速度极慢。在相似性搜索中,搜索速度和搜索质量(准确性)之间总是存Flat 索引提供最高准确性,但搜索速度较慢。在相似性搜索中,搜索速度和搜索质量之间需要找到平衡点。对于 Flat 索引,这意味着在搜索时间和搜索质量之间做出选择。

平面索引的搜索质量是100%,搜索速度是0%。
这里完全没有优化的搜索速度,这将适合许多较小索引的用例 — 或者搜索时间无关紧要的场景。但是,其他用例需要在速度和质量之间取得更好的平衡。为了提高搜索速度,可以采用两种主要方法:
- 减小向量大小 — 通过降维或减少表示向量值的位数。
- 缩小搜索范围 — 可以通过聚类或根据某些属性、相似性或距离将向量组织成树状结构,并限制搜索到最近的聚类或通过最相似的分支进行筛选。
这些方法意味着不再执行全分辨率数据集的穷尽搜索,而是采用近似最近邻(ANN)搜索。
所以,产生的是一个更平衡的组合,既优先考虑搜索速度也考虑搜索时间。

通常搜索速度和搜索质量两者更平衡的组合
Locality Sensitive Hashing局部敏感哈希
LSH的性能范围广泛,严重依赖于设定的参数
局部敏感哈希(LSH)通过使用哈希函数将向量分组到桶中,这些函数旨在最大化哈希冲突,而非像传统哈希函数那样最小化冲突。这种方法允许相似的向量被分组在一起,便于搜索时快速找到最接近的匹配。
想象有一个Python字典。当在字典中创建一个新的键值对时,使用一个哈希函数来哈希键。这个键的哈希值决定了存储其相应值的“桶”:
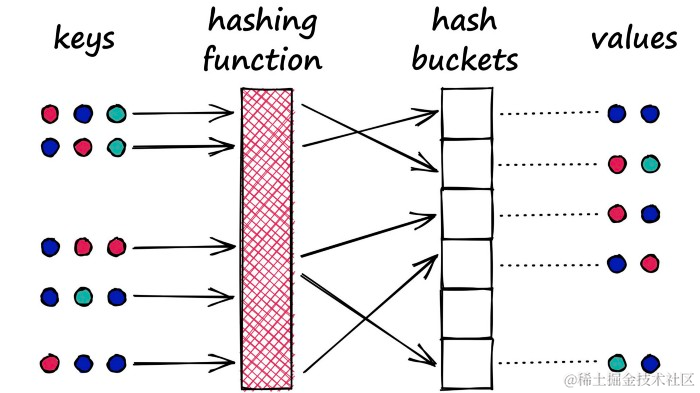
典型的字典对象的哈希函数将尝试最小化哈希冲突,目标是为每个桶分配一个值。
Python字典是使用典型哈希函数的哈希表的一个例子,该函数最小化哈希冲突,即两个不同的对象(键)产生相同的哈希。
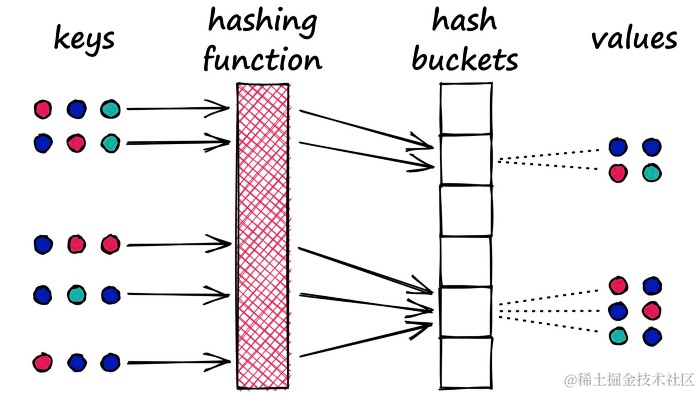
为什么LSH要最大化冲突?对于搜索,使用LSH将相似的对象分组在一起。当引入一个新的查询对象(或向量)时,LSH算法可以用来找到最接近的匹配组:
 )
)
LSH哈希函数尝试最大化哈希冲突产生向量分组。
实现局部敏感哈希(LSH)
在 Faiss 中实现 LSH 索引相对简单。首先,初始化一个 IndexLSH 对象,指定向量维度 d 和 nbits 参数,然后添加向量。nbits 参数决定了哈希向量的分辨率,影响索引的准确性和搜索速度。
nbits = d*4 # 分辨率
index = faiss.IndexLSH(d, nbits)
index.add(wb)
# 搜索
D, I = index.search(xq, k)
nbits参数指的是哈希向量的“分辨率”。更高的值意味着更高的准确性,但代价是更多的内存和更慢的搜索速度。

当
d为128时,IndexLSH的召回率得分。注意,要获得更高的召回性能,需要大幅度增加num_bits的值。要达到90%的召回率,使用64d,即 64 × 128 = 8192 64 \times 128 = 8192 64×128=8192。
LSH 提供了广泛的性能范围,其性能严重依赖于参数设置。高分辨率(高 nbits)可以提高召回率,但会增加内存使用和搜索时间。对于高维数据,LSH 的性能可能不佳,尤其是当向量维度较大时。随着 d 的增加,存储的向量变得更大,这可能导致搜索时间过长。
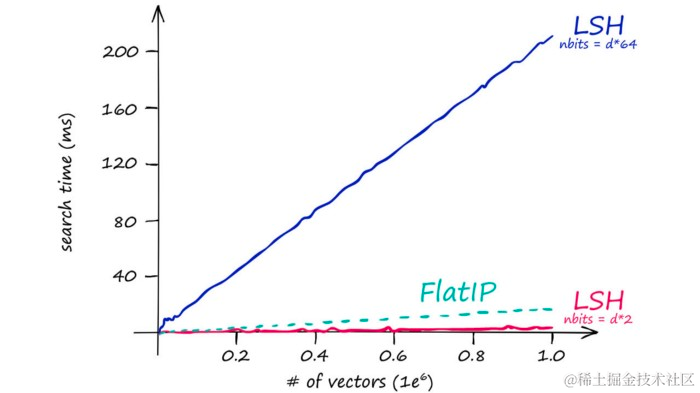
不同
nbits值下IndexLSH的搜索时间,与平面IP索引相比较。
这反映在索引内存大小上:
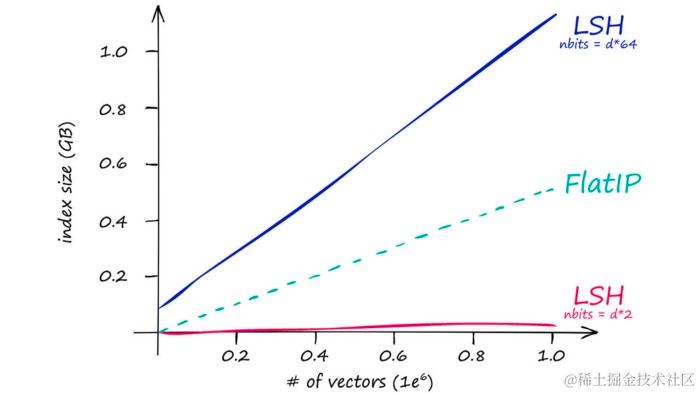
不同
nbits值下IndexLSH的索引大小,与平面IP索引相比较。
当处理大向量维度(如 128)时,IndexLSH 可能不再适用。在这种情况下,更适合的索引类型可能是 HNSW,特别是对于大型数据集和需要高效率的搜索场景。
Hierarchical Navigable Small World Graphs分层可导航小世界图
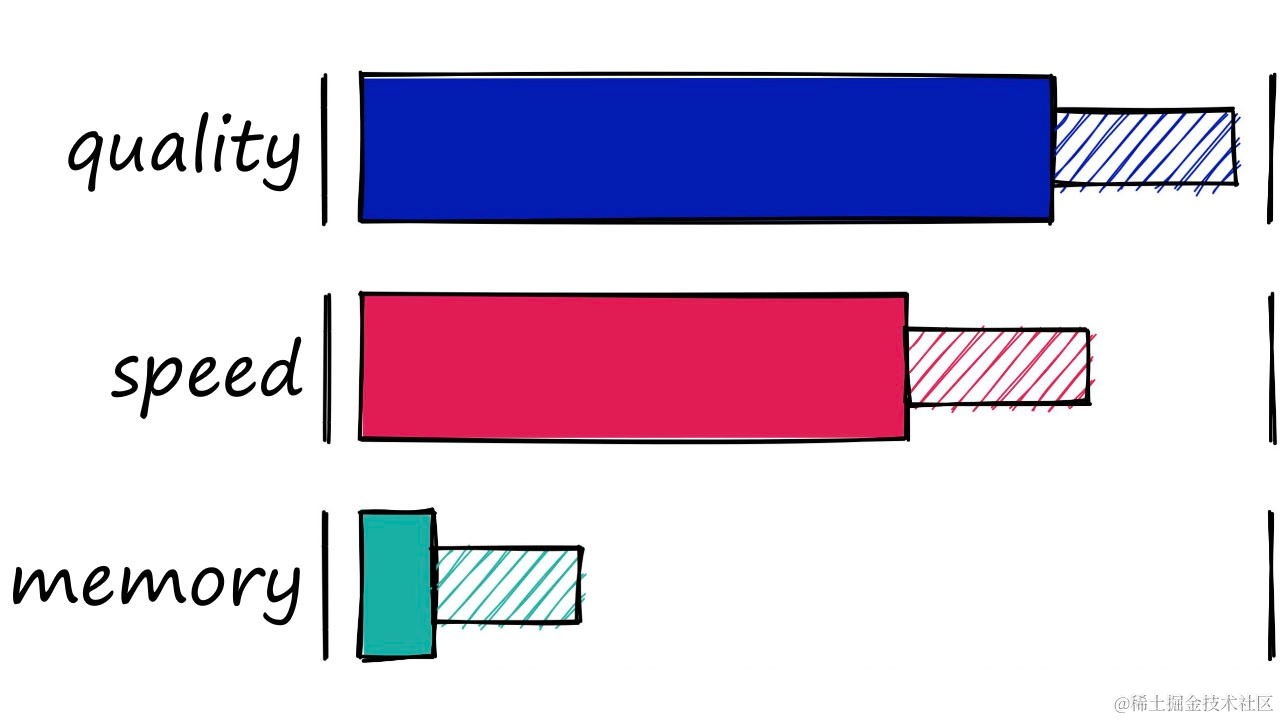
HNSW — 出色的搜索质量,良好的搜索速度且索引大小相当可观
HNSW 是一种高性能的索引类型,适用于大型数据集,特别是在高维度下。它基于可导航小世界(NSW)图,通过构建多层图结构来提高搜索速度和质量。
“NSW”部分是由于这些图中的顶点都具有到图中所有其他顶点的非常短的平均路径长度 — 尽管它们并没有直接连接。
以Facebook为例 — 在2016年,可以将每个用户(一个顶点)连接到他们的Facebook好友(最近邻居)。尽管有15.9亿活跃用户,从一个用户到另一个用户穿越图所需的平均步骤(或跳数)仅为3.57。

可视化一个NSW图。每个点最多只离另一个点四跳远。
Facebook只是广阔网络中高连通性的一个例子 — 也就是所谓的NSW图。
在高层次上,HNSW图是通过获取NSW图并将它们分解为多层构建的。每增加一个层级就消除了顶点之间的中间连接。
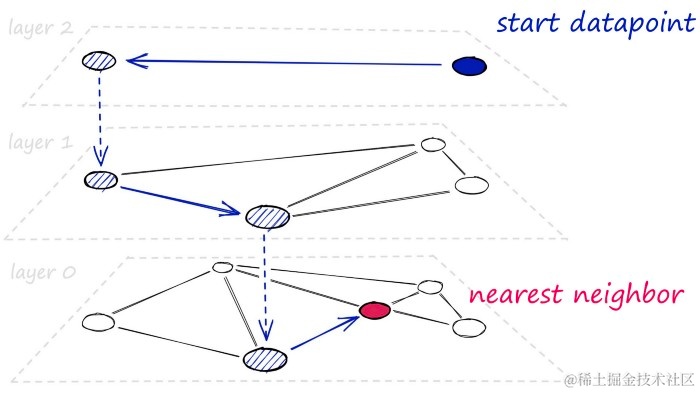
使用HNSW,将网络分解为几个层,在搜索期间遍历这些层。
对于具有更高维度的大型数据集 — HNSW图是可以使用的表现得最好的索引之一。
实现HNSW
要在Faiss中构建和搜索一个平面HNSW索引,所需要的只是IndexHNSWFlat:
# # 设置 HNSW 索引参数
M = 64 # 每个顶点的邻居数量
ef_search = 32 # 搜索深度
ef_construction = 64 # 构建深度
# 初始化索引(假设 d == 128)
index = faiss.IndexHNSWFlat(d, M)
index.hnsw.efConstruction = ef_construction
index.hnsw.efSearch = ef_search
index.add(wb)
# 搜索
D, I = index.search(wb, k)
可以看到,有三个关键参数来修改索引的性能。
M— 每个顶点将连接到的最近邻居的数量。efSearch— 在搜索期间,将探索多少个层间的入口点。efConstruction— 在构建索引时将探索多少个入口点。
每个参数都可以增加以提高搜索质量:
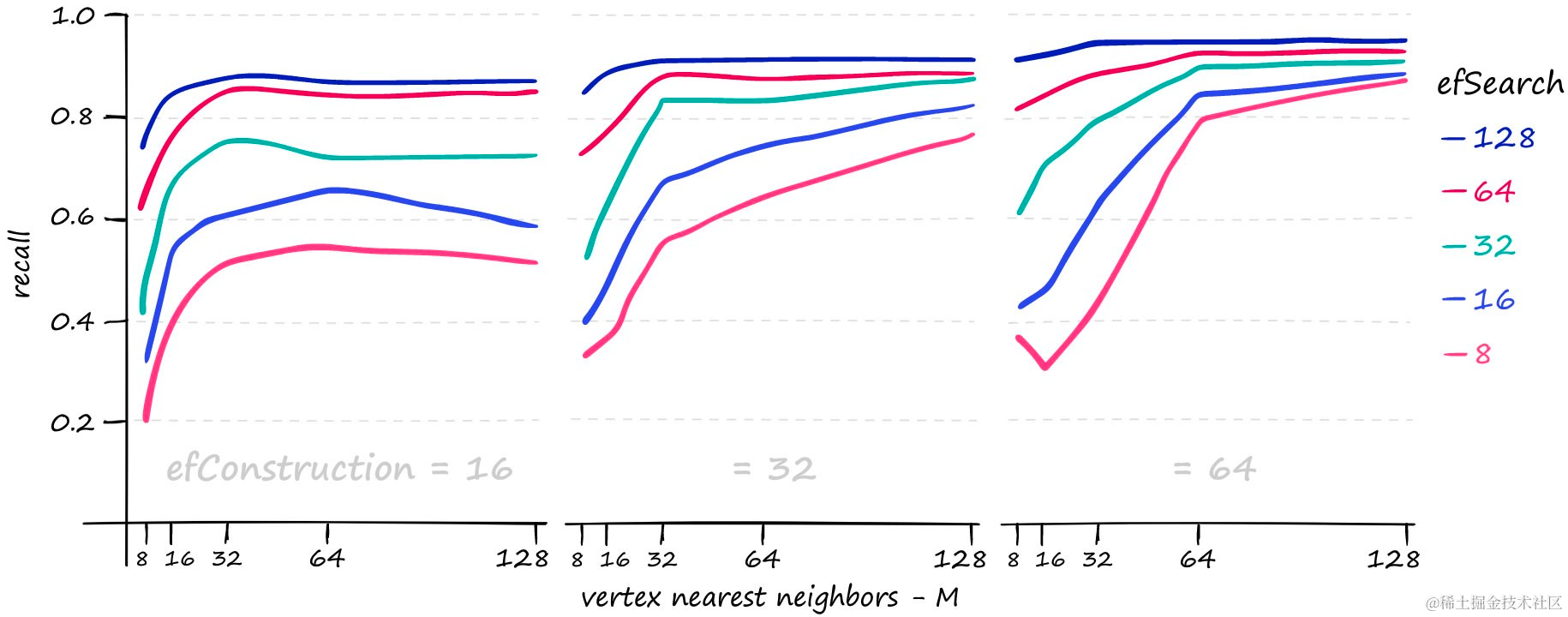
在Sift1M数据集上,不同
efConstruction、efSearch和M值的召回值。
M和efSearch对搜索时间有更大的影响 — efConstruction主要增加了索引构建时间(意味着更慢的index.add),但在更高的M值和更高的查询量时,确实看到efConstruction对搜索时间也有影响。
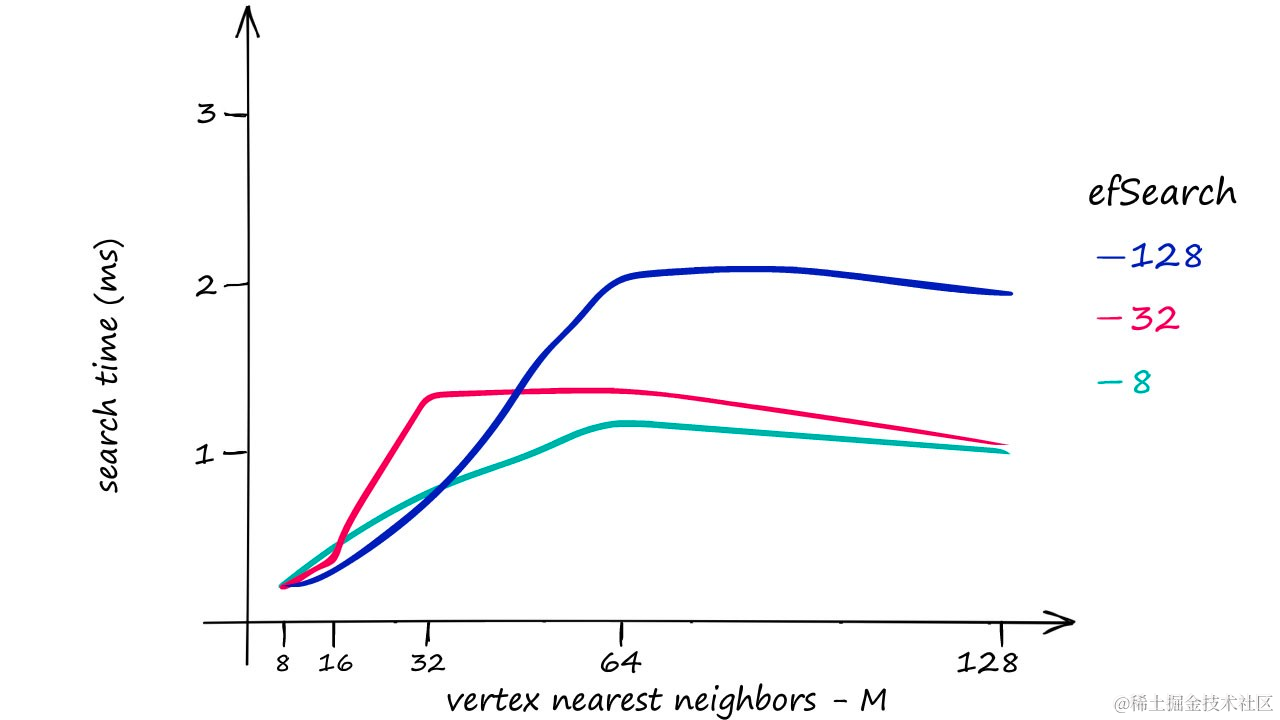
在完整的Sift1M数据集上,不同
M和efSearch值的搜索时间。
虽然 HNSW 提供高效的搜索,但其索引大小可能成为一个问题,尤其是在内存受限的环境中。例如,对于 Sift1M 数据集,使用较大的 M 值可能需要超过 1.6GB 的内存。
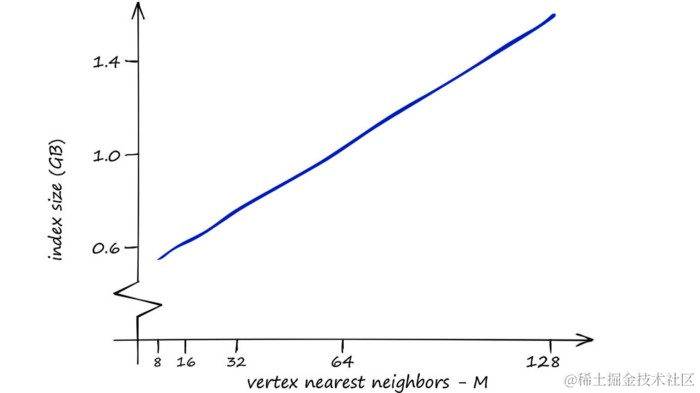
在Sift1M数据集上,不同
M值的索引内存使用情况。
然而,可以增加另外两个参数 — efSearch和efConstruction,这俩参数不影响索引的内存占用。
因此,当RAM不是限制因素时,HNSW是一个很好的平衡索引,可以通过增加三个参数来推动它更偏向于搜索质量。
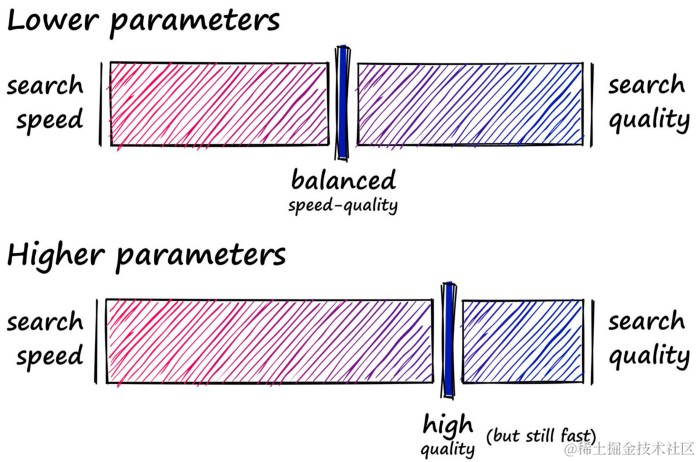
可以使用较低的参数组来平衡优先考虑稍微更快的搜索速度和良好的搜索质量,或者使用较高的参数组以稍微慢一点的搜索速度获得高质量的搜索。
HNSW 是一个强大且高效的索引,特别适合于处理高维大型数据集。通过调整其参数,可以在搜索速度和质量之间找到平衡。
Inverted File Index倒排文件索引
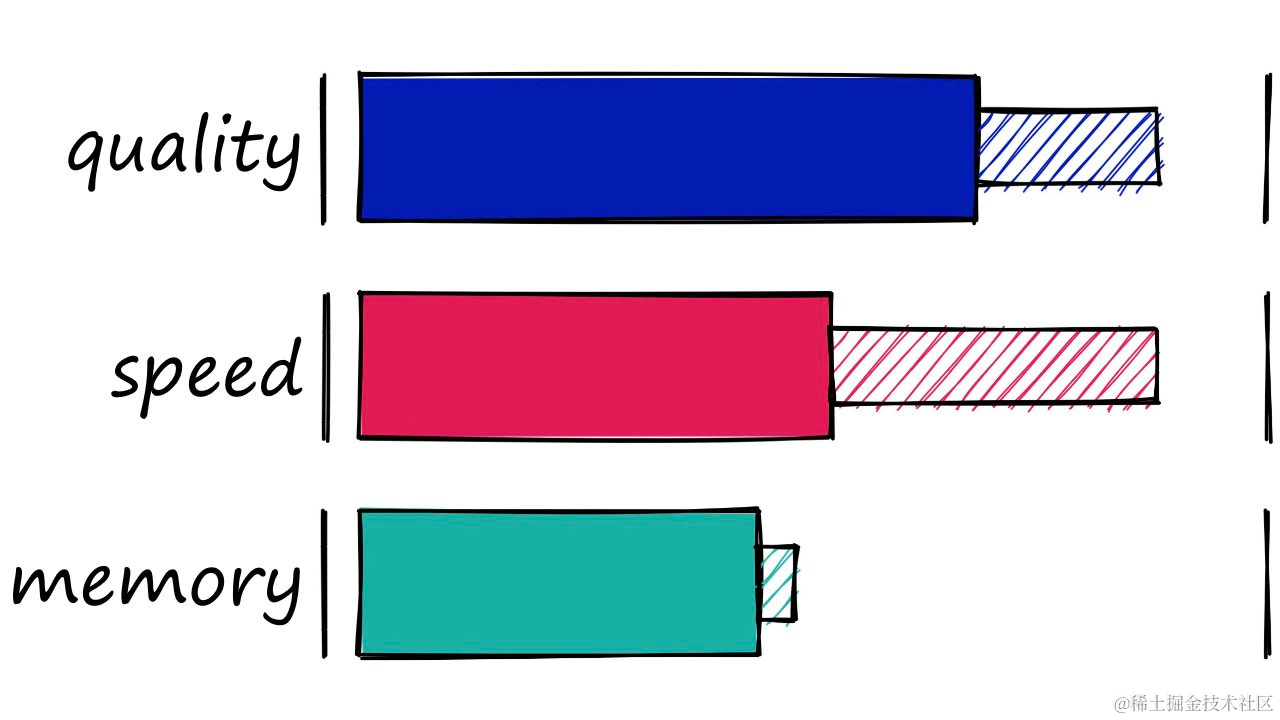
倒排文件索引(IVF)以其出色的搜索质量、良好的搜索速度和合理的内存使用而著称。条形图中的“半填充”部分代表了在修改索引参数时遇到的性能范围。
倒排文件索引(IVF)以其出色的搜索质量、良好的搜索速度和合理的内存使用而著称。它通过聚类技术显著减少了搜索范围,使得在处理大型数据集时更为高效。
IVF基于沃罗诺伊图的概念 — 也称为狄利克雷镶嵌。将高维向量空间分割成多个单元。每个单元由一个中心点定义,该中心点是该单元内所有向量的最近邻居。查询向量被限制在其所在的单元内,从而大大减少了搜索空间。
沃罗诺伊单元是如何构建的 — 上面有三个中心点,从而形成了三个沃罗诺伊单元。然后,每个给定单元内的数据点将被分配给相应的中心点。 现在,每个数据点都将被包含在一个单元内 — 并被分配给相应的中心点。
就像其他索引一样,引入了一个查询向量xq — 这个查询向量必须落在一个单元内,此时将搜索范围限制在那个单元内。但如果查询向量落在单元的边缘附近,就会出现问题 — 它最近的其他数据点很可能包含在相邻的单元内,将这称为边缘问题:

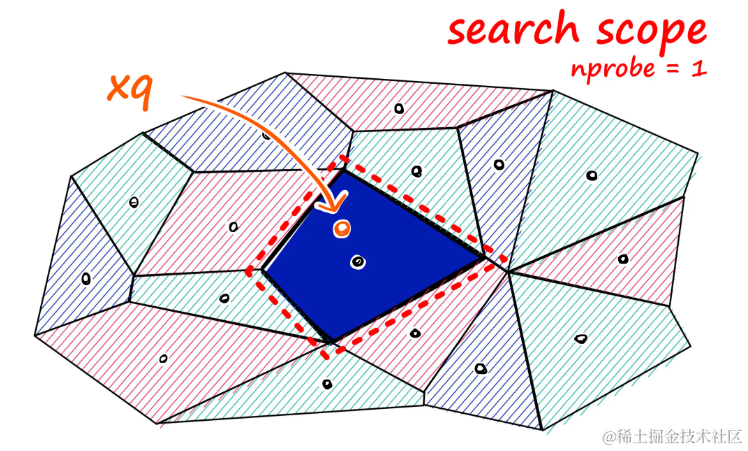
查询向量
xq落在了洋红色单元的边缘上。尽管它更接近于青绿色单元中的数据点,但如果nprobe == 1,这意味着将搜索范围限制在洋红色单元内。
为了缓解这个问题并提高搜索质量,可以增加一个称为nprobe值的索引参数。通过nprobe,可以设置要搜索的单元数量。
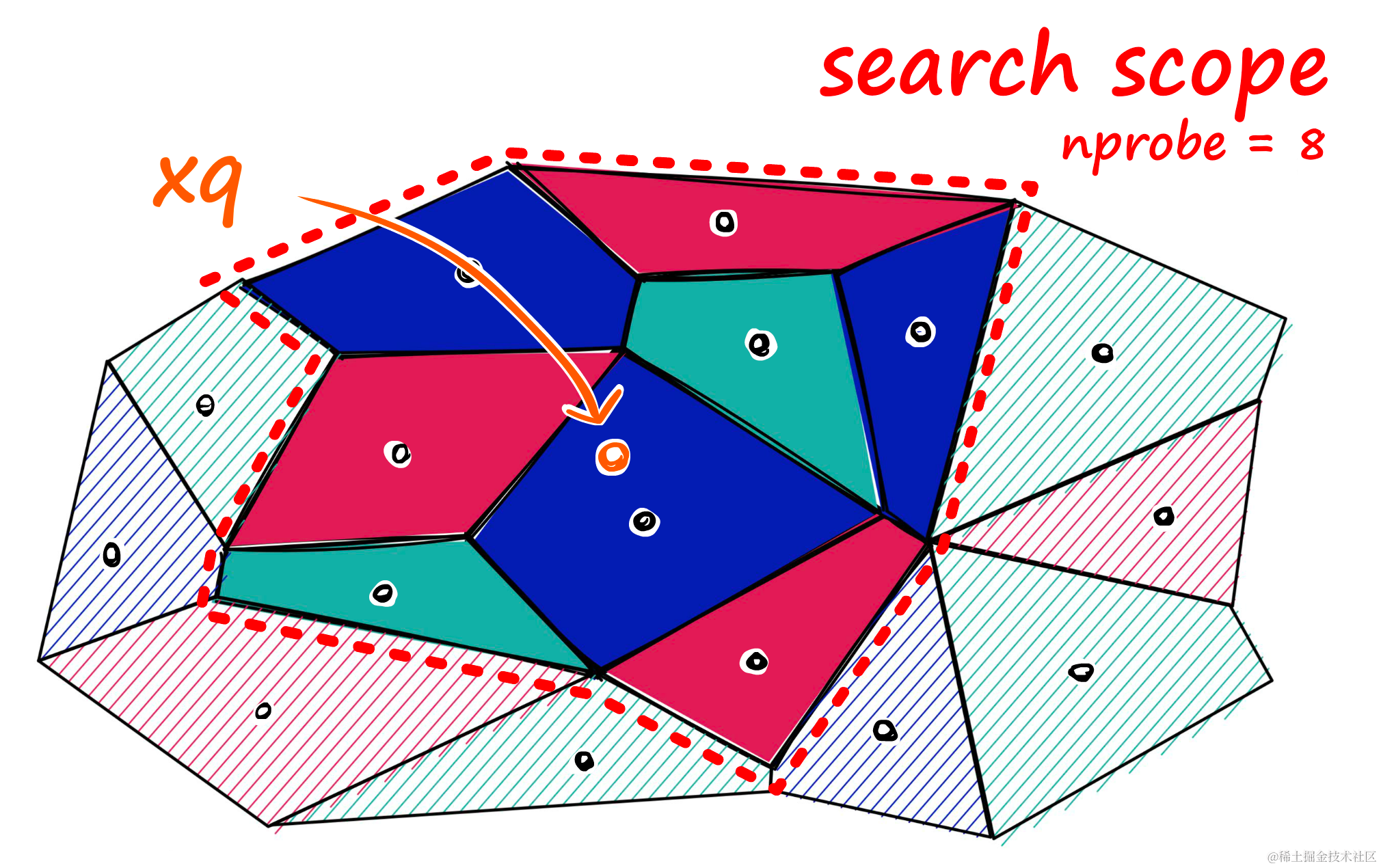
增加nprobe会增加搜索范围。
实现IVF
要实现IVF索引并在搜索中使用它,可以使用IndexIVFFlat:
nlist = 128 # 聚类单元数量
quantizer = faiss.IndexFlatIP(d) # 向量存储和比较方式
index = faiss.IndexIVFFlat(quantizer, d, nlist)
index.train(data) # 训练索引以聚类
index.add(data)
index.nprobe = 8 # 设置要搜索的单元数量
D, I = index.search(xq, k)
有两个参数可以调整。
nprobe— 要搜索的单元格数量nlist— 要创建的单元格数量
nlist值较高意味着必须将向量与更多的中心点向量进行比较 — 但在选择了最近的中心点单元格进行搜索后,每个单元格内的向量数量会减少。因此,增加nlist以优先考虑搜索速度。
对于nprobe,发现情况正好相反。增加nprobe会增加搜索范围 — 从而优先考虑搜索质量。

使用不同
nprobe和nlist值的 IVF 搜索时间和召回率。
在内存方面,IndexIVFFlat是相当高效的 — 修改nprobe不会影响这一点。nlist对内存使用的影响也很小 — 更高的nlist意味着略微增加的内存需求。
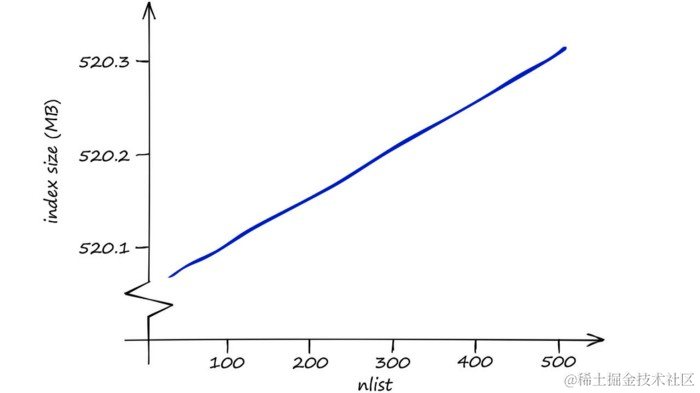
索引的内存使用情况仅受
nlist参数影响。然而,对于 Sift1M 数据集,索引大小仅发生很小的变化
IVF 的一个潜在问题是所谓的“边缘问题”,即查询向量落在单元的边缘附近时,可能无法找到最接近的数据点。通过增加 nprobe,可以缓解这个问题并提高搜索质量。
性能对比
在 M1 芯片(8核CPU,8GB内存)的硬件环境下,对四种主要索引类型(Flat、LSH、HNSW、IVF)进行了性能测试。这些测试旨在评估不同索引在处理 Sift1M 数据集(128维,1M条记录)时的表现。
| 索引 | 内存 (MB) | 查询时间 (ms) | 召回率 | 注意事项 |
|---|---|---|---|---|
| Flat(L2 或 IP) | ~500 | ~18 | 1.0 | 适用于小数据集或查询时间不相关的情况 |
| LSH | 20 - 600 | 1.7 - 30 | 0.4 - 0.85 | 最适用于低维数据或小数据集 |
| HNSW | 600 - 1600 | 0.6 - 2.1 | 0.5 - 0.95 | 质量非常好,速度快,但内存使用量大 |
| IVF | ~520 | 1 - 9 | 0.7 - 0.95 | 良好的可扩展选项。高质量,速度合理,内存使用合理 |
上述数据是基于 Sift1M 数据集上进行的 20 次测试的平均结果,涵盖了不同参数设置。测试结果已排除不切实际的参数配置
这些结果为选择最适合您用例的索引提供了参考。请注意,实际应用中的性能可能因数据集和参数设置的不同而有所差异。
参考
- Pinecone 向量索引教程 - 了解更多关于向量索引的详细信息。
- ANN-benchmarks repo - E Bernhardsson 维护的用于评估近似最近邻搜索算法的代码库。
- Three and a half degrees of separation - S Edunov 等人关于 Facebook 社交网络连接性的研究。