图的基本概念

图的定义：
图是由顶点的非空有穷集合与顶点之间关系（边或弧）的集合构成的结构，通常表示为：G=（V,E），其中V为顶点集合，E为关系（边或弧）的集合。

图的分类：
无向图：对于（vi，vj）∈E，必有（vj，vi）∈ E，并且偶对中顶点的前后顺序无关。
有向图：<vi,vj>∈E是顶点的有序偶对。
网：与边有关的数据称为权，边上带权的图称为网。
顶点的度：
依附于顶点Vi的边的数目，称为TD（i）；
对于有向图而言：
顶点的出度：以顶点vi为出发点的边的数目：记为OD（vi）；
顶点的入度：以顶点vi为终止点的边的数目，记为ID（vi）；
TD（vi）=OD（vi）+ID（vi）；

顶点和边关系：
①具有n个顶点的无向图最多有n（n-1）/ 2 条边。
②具有n个顶点的有向图最多有n（n-1）条边。
边的数目达到最大的图称为完全图，边的数目达到或接近最大的图称为稠密图，否则，称为稀疏图。

路径和路径长度：
顶点vx和vy之间有路径P（vx，vy）的充分必要条件是：存在顶点序列vx，vi1，vi2，……，vim，vy，并且序列中相邻两个顶点构成的顶点偶对分别为图中的一条边。
出发点与终止点相同的路径称为回路或环。
顶点序列中顶点不重复出现的路径称为简单路径。
不带权的图的路径长度是指路径上所经过的边的数目，带权图的路径长度是指路径上经过的边上的权值之和。

子图：
如下图所示,G1’和G2’就是G的子图。
无向图的连通：
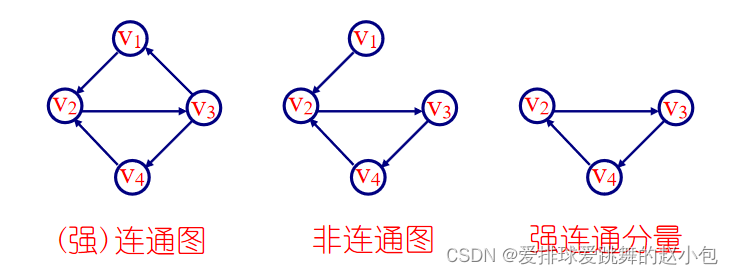
无向图中顶点vi到vj有路径，则称顶点vi和vj是连通的。若无向图中任意两个顶点都有连通，则称该无向图是连通的（称为连通图）。
连通分量：无向图中的极大连通子图。

有向图的连通：若有向图中顶点vi到vj有路径，并且顶点vj到vi也有路径，则称顶点vi与vj是连通的。若有向图中任意两个顶点都连通，则称该有向图是强连通的。
强连通分量：有向图中的极大强连通子图。
生成树：包含n个顶点和n-1条边的极小连通子图称为G的一个生成树。

生成树的性质：
1.包含n个顶点的图：连通且仅有n-1条边

=无回路且仅有n-1条边

=无回路且连通

=是一棵树
2.如果n个顶点的图中只要有少于n-1条边，图将不连通
3.如果n个顶点的图中有多于n-1条边，图将有环（回路）
4.一般，生成树不唯一。

图的存储方法

因为期末考试不考图的编程题，所以这里简单介绍一下即可：

邻接矩阵：

核心思想 ：采用两个数组存储一个图。

1. 定义一个一维数组VERTEX【0……n-1】存放图中所有顶点的数据信息。
2. 定义一个二维数组A【0……n-1,0……n-1】存放图中所有顶点之间关系的信息（即邻接矩阵）
   
   例如：
   邻接矩阵特点：

①无向图的邻接矩阵一定是一个对称矩阵 。
②不带权的有向图的邻接矩阵一般是稀疏矩阵。
③无向图的邻接矩阵的第i行（或第i列）非0或非∞元素的个数为第 i个顶点的度数。
④有向图的邻接矩阵的第i行非0或非∞元素的个数为第i个顶点的出度；第i列非0或非∞元素的个数为第i个顶点的入度。

邻接表

核心思想：建立n个线性链表存储该图
①顶点结点：每个链表前面设置一个头结点，用来存放一个顶点的数据信息，称之为顶点节点。其构造为其中，vertex存放某个顶点的数据信息；link存放某个链表中第一个结点的地址。

②边结点：第i个链表中的每一个链结点（边结点）表示以第i个顶点为出发点的一条边，边结点构造为：weight域为权值域（若图不带权，则无此域）；
adjvex域存放以第i个顶点为出发点的边的另一端点在头结点数组中的位置。

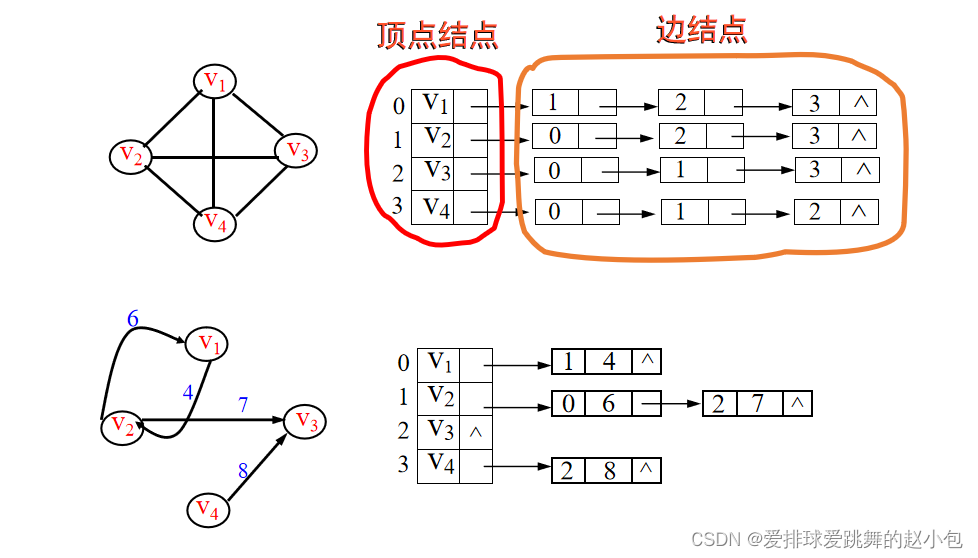
特点：
①无向图的第i个链表中边结点个数是第i个顶点的度数。

②有向图的第i个链表中边结点个数是第i个顶点的出度。

③无向图的边结点个数一定为偶数，边结点个数为奇数的图一定是有向图。

图的遍历

深度优先（DFS）

直接上个图就行了：

为了区分哪些顶点被访问过，哪些没被访问，可以设置一个数组visit，visit[i]=0，表示没有被访问过，visit[i]=1，已经被访问过。

算法分析：
若采用邻接表存储该图，则时间复杂度为O(n+e)。
若采用邻接矩阵存储，则时间复杂度为O(n²）

广度优先（BFS）

类似于树的层序遍历。

时间复杂度和空间复杂度同DFS。

最小生成树

带权连通图中，总的权值之和最小的带权生成树为 最小生成树 。最小生成树也称最小代价生成树,或最小花费生成树。

Prim算法

设G=（V,GE）为具有n个顶点的带权连通图，T=（U,TE）为生成的最小生成树，初始时，TE为空，U={v}，v∈V。
依次在G中选择一条一个顶点仅在V中，另一个顶点在U中，并且权值最小的边加入集合TE，同时将该边仅在V中的那个顶点加入集合U。重复上述过程n-1次，是的U=V，此时T为G的最小生成树。

Kruskal算法

从G中选一条当前为选择过的，且边上的权值最小的边加入TE，若加入TE后使得T未产生回路，则本次选择有效，如使得T产生回路，则本次选择无效，放弃本次选择的边。重复上述选择过程直到TE中包含了G的n-1条边，此时的T为G的最小生成树。

最短路径问题

Dijkstra算法（单源点问题）
1.图的存储：
以0~1分别代表n个顶点，采用邻接矩阵存储该图，有

2.几个必要的数组设置：
①设置一个标志数组s[0……n-1]记录源点v到图中哪些顶点的最短路径已经找到。有：

②设置数组dist[0……n-1]分别记录源点v到图中各顶点的最短路径的路径长度，其中，dist[i]记录源点到顶点i的最短路径长度。初始时，dist数组的值为邻接矩阵第v行的n个元素值。
③设置数组path[0……n-1]分别记录源点v到图中各顶点的最短路径所经过的顶点序列，其中，path[i]记录源点到顶点i的路径。

自然语言表达：

其中，初值为：

v为原点。