一、首先给出biquad的Z变换函数为:
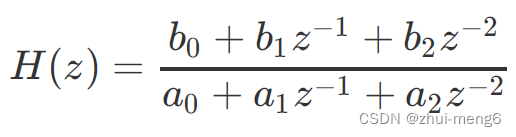
为了计算方便可对上式进行归一化处理,分子分母同时除以a0,则得出如下:
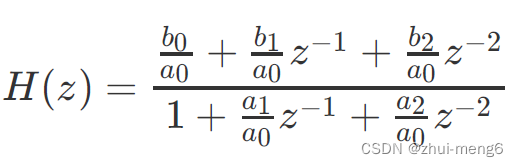
对应的差分方程为:
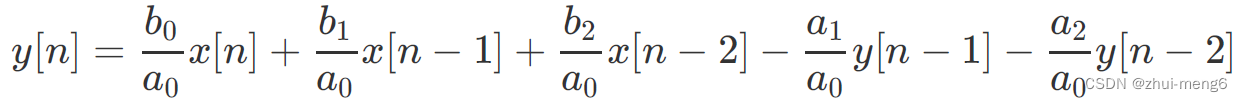
二、用户定义参数如下
#ifndef LN2
#define LN2 0.69314718055994530942
#endif
#ifndef PI
#define PI 3.14159265358979323846
#endif
Fs:采样率
f0:中心频率
dbGain:即dbBoost,增益
bandwidth:带宽
三、中间变量如下:
A = pow(10, dbGain /40);
omega = 2 * PI * f0/Fs;
sin = sin(omega);
cos=cos(omega);
alpha = sin * sinh(LN2 /2 * bandwidth * omega /sin);
beta = sqrt(A + A);
四、系数计算:
4.1、低通滤波器
H(s) = 1 / (s^2 + s/Q + 1)
b0 = (1 - cos) /2;
b1 = 1 - cos;
b2 = (1 - cos) /2;
a0 = 1 + alpha;
a1 = -2 * cos;
a2 = 1 - alpha;
4.2、高通滤波器
H(s) = s^2 / (s^2 + s/Q + 1)
b0 = (1 + cos) /2;
b1 = -(1 + cos);
b2 = (1 + cos) /2;
a0 = 1 + alpha;
a1 = -2 * cos;
a2 = 1 - alpha;
4.3、带通滤波器
H(s) = s / (s^2 + s/Q + 1)//(constant 0 dB peak gain)
b0 = alpha;
b1 = 0;
b2 = -alpha;
a0 = 1 + alpha;
a1 = -2 * cos;
a2 = 1 - alpha;
4.4、NOTCH滤波器—Sigma中未介绍,可参考该公式
H(s) = (s^2 + 1) / (s^2 + s/Q + 1)
b0 = 1;
b1 = -2 * cos;
b2 = 1;
a0 = 1 + alpha;
a1 = -2 * cos;
a2 = 1 - alpha;
4.5、peaking滤波器—尖峰滤波,Sigma中未介绍,可参考该公式
H(s) = (s^2 + s*(A/Q) + 1) / (s^2 + s/(A*Q) + 1)
b0 = 1 + (alpha * A);
b1 = -2 * cos;
b2 = 1 - (alpha * A);
a0 = 1 + (alpha /A);
a1 = -2 * cos;
a2 = 1 - (alpha /A);
4.6、低架滤波
H(s) = A * (s^2 + (sqrt(A)/Q)s + A)/(As^2 + (sqrt(A)/Q)*s + 1)
b0 = A * ((A + 1) - (A - 1) * cos + beta * sin);
b1 = 2 * A * ((A - 1) - (A + 1) * cos);
b2 = A * ((A + 1) - (A - 1) * cos - beta * sin);
a0 = (A + 1) + (A - 1) * cos + beta * sin;
a1 = -2 * ((A - 1) + (A + 1) * cos);
a2 = (A + 1) + (A - 1) * cos - beta * sin;
4.7、高架滤波
H(s) = A * (A*s^2 + (sqrt(A)/Q)*s + 1)/(s^2 + (sqrt(A)/Q)*s + A)
b0 = A * ((A + 1) + (A - 1) * cos + beta * sin);
b1 = -2 * A * ((A - 1) + (A + 1) * cos);
b2 = A * ((A + 1) + (A - 1) * cos - beta * sin);
a0 = (A + 1) - (A - 1) * cos + beta * sin;
a1 = 2 * ((A - 1) - (A + 1) * cos);
a2 = (A + 1) - (A - 1) * cos - beta * sin;
参考来源:https://www.cnblogs.com/fellow1988/p/9136346.html
五、频响曲线
var phi=pow((sin(2.0PIf0/(2.0*FS))),2);
var r=pow(b0+b1+b2,2.0)-4.0*(b0b1+4.0b0b2+b1b2)phi+16.0b0b2phiphi(pow(1.0+a1+a2,2.0)-4.0(a1+4.0a1a2)phi+16.0a2phiphi);
r=(r<0)?0:r;
return sqrt( r );