- 什么是最小公倍数?
最小公倍数是指两个或多个整数共有的最小正整数倍数。
- 如何求一组数据的最小公倍数(Least Common Multiple,简称LCM)?
LCM = 这组数据的公倍数 这组数据的最大公约数 (Greatest Common Divisor,简称GCD)
例如:两个数a和b,它们的最小公倍数lcm(a, b)可以通过它们的乘积除以它们的最大公约数gcd(a, b)来得到,即:lcm(a,b) = ,所以求最小公倍数的问题重点就转换成了求最大公约数。
- 如何求最大公约数?欧几里得算法: gcd(a,b)
欧几里得算法,又称为“辗转相除”法,顾名思义, 这个算法的核心思想就是不断的去除。它是迄今为止已知的最古老的算法,距今(2024年)已经有2324年了,这个算法可用于快速计算两个数字的最大公约数的。
定理:a 和 b两个整数的最大公约数等于 b 与 a%b 的最大公约数。
通过定理的表述,我们发现,问题规模从[b,a] 缩小到了为了[b, a%b],即问题规模从原始规模缩小到了原始规模的子规模,但是问题的解没有变,也就是说,子规模中蕴含着原始问题的解。
所以,我们要证明两点:
第一: 在子规模中包含原始规模的解;
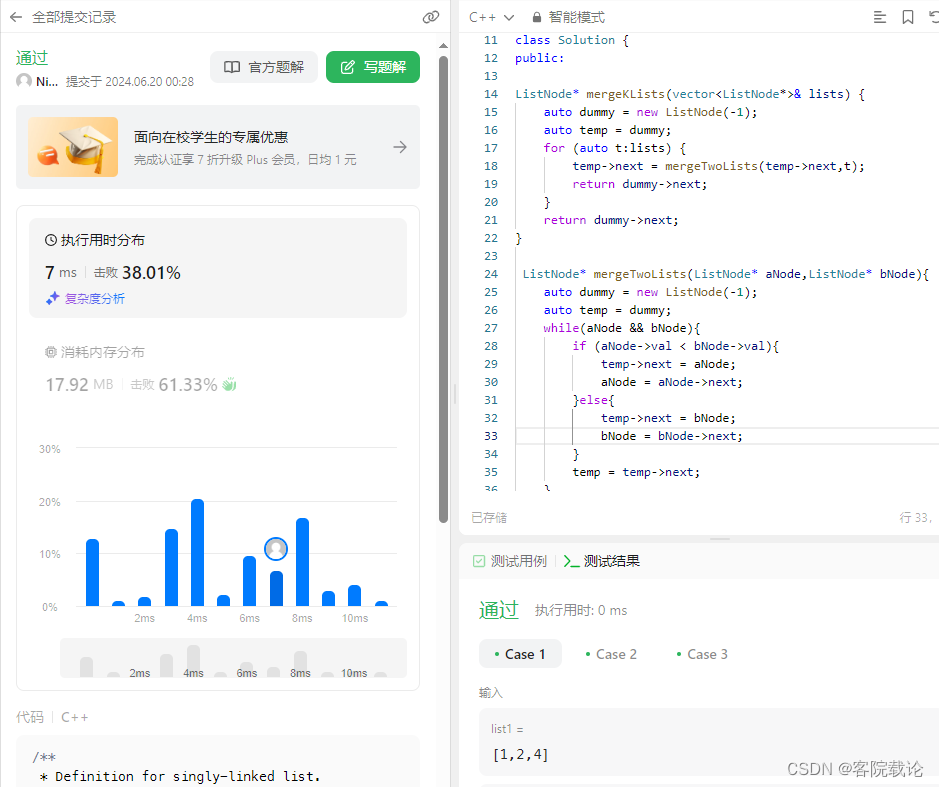
第二:在子规模中找到的答案就是最大公约数,而不仅仅是公约数之一。
证明问题一:
如果我们能证明 a 和 b 的最大公约数,同时也能被 a % b 整除 (是a%b的因子),那么就可以说原始规模的问题的解是包含在子规模中的。
设 a和b 的最大公约数 为c :即 c = gcd(a,b), 则: a = cx, b = cy;
假设: a % b = r;
那么:r = a - kb = cx - kcy = c(x-ky)
所以:c 也是 r 的因子。
证明问题二:
如果我们想证明 gcd(b, a%b ) 得到的就是最大公约数,那么只要证明 b 和 (a%b)除了c之外再无公约数即可,又因为b = cy, a%b = c(x-ky) , 即只要能能证明 y 和 (x-ky)互为素数即可。
假设: gcd(x-ky, y) = d;
则 y = nd,
x-ky = md ; x = md+ky
x = (m+kn)d;
所以,a 和 b 可以表示成: a = cd(kn +m), b = cdn, 进而可知:gcd(a,b) >= cd ,
又因为 gcd(a,b) = c,
所以 d=1, y 和 (x-ky)的公约数为1, 说明y 和(x-ky) 互为素数。
题目1:2520是最小的能够被1到10整除的正数。最小的能够被1到20整除的正数是多少?
题目分析:
根据题目描述,就是要找到1到20的最小公倍数。
代码实现:
#include <stdio.h>
//求整数a 和 b 的最大公约数
int gcd(int a, int b){
if(b == 0) return a;
return gcd(b, a%b);
}
//求整数a 和 b 的最小公倍数
long lcm(long a, long b){
return a*b / gcd(a, b);
}
//求1到20 的最小公倍数
int main(){
long long ans = 1;
for(int i = 2; i <= 20; i++) ans = lcm(ans, i);
printf("%lld\n", ans);
return 0;
}小技巧:
在上述代码中,函数 long lcm(long a, long b) ,有两点需要注意,第一,为了不出现数据溢出现象,数据类型定义为long, 第二, 同样是为了不出现数据溢出, a*b/gcd(a,b) 这个运算语句,应该改为先 a /gcd(a, b) * b, 即先执行除法再做乘法,以免先乘法生产一个超出数据范围的大数据。
//求整数a 和 b 的最小公倍数
long lcm(long a, long b){
return a / gcd(a, b) * b;
}