CFD
定常流动与非定常流动
定常流动:流体流动过程中各物理量均与时间无关;
非定常流动:流体流动过程中某个或某些物理量与时间有关.
运动黏度
运动粘度定义: v = μ ρ v = \frac{\mu}{\rho} v=ρμ,其中 μ \mu μ表示粘度,
黏性应力 τ \tau τ
τ = μ d u d y \tau=\mu\frac{du}{dy} τ=μdydu(单位是Pa),其中 μ \mu μ是黏度,表示黏性应力和速度的梯度成正比.而应变率是 ∂ u ∂ y \frac{\partial u}{\partial y} ∂y∂u.
雷诺数
雷诺数是一个没有单位的无量纲数,指的是流体中惯性力和粘性力的比值.
R
e
=
惯性力
粘性力
=
U
×
d
v
Re=\frac{惯性力}{粘性力}=\frac{U\times d}{v}
Re=粘性力惯性力=vU×d
其中U是特征速度,d是特征长度,v是运动粘度.
雷诺数越小,说明粘性力与惯性力相比,粘性力占主导地位,流体就黏糊糊的;雷诺数越大,说明惯性力占主导地位,流体就越清爽。
层流与湍流
湍流就是雷诺数大的状态,也就是流体粒子的惯性完全超越了粘性力的作用,处于自由运动的状态.
湍流其实就是流速很快的流体,因为流速很快的话流体就会炸开,而流速很快的话势必要求流体很清爽,清爽的流体的黏性力很小,对应的雷诺数很大,所以湍流的雷诺数很大.
动力粘度(dynamic viscosity)和运动粘度(kinematic viscosity)
**动力粘度
μ
\mu
μ**的关系式:
τ
=
μ
d
u
d
y
\tau=\mu\frac{du}{dy}
τ=μdydu
式中
τ
\tau
τ是应力,单位是
P
a
=
N
/
m
2
Pa=N/m^2
Pa=N/m2.
d
u
d
y
\frac{du}{dy}
dydu为速度梯度, 单位是
m
s
⋅
1
m
=
1
s
\frac{m}{s}\cdot\frac{1}{m}=\frac{1}{s}
sm⋅m1=s1.
而**运动粘度
ν
\nu
ν**的定义式:
ν
=
μ
ρ
\nu = \frac{\mu}{\rho}
ν=ρμ
理解:动力粘度是流体抵抗流动的阻力大小;运动粘度不受流体密度的影响.
摩尔质量
是每一摩尔化学元素或者化合物的质量,单位是kg/mol;对于单个原子,其摩尔质量在数值上等于其相对原子质量.
连续介质假设
将流体看作是连续、均匀、无限细小的介质,忽略了流体内部的微观结构和分子运动。即假设流体在宏观上是连续的,可以用一系列连续的物理量来描述.
牛顿流体与非牛顿流体
牛顿内摩擦定律: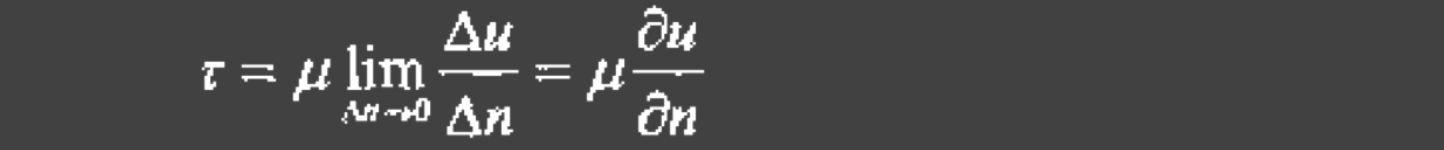
牛顿内摩擦应力和单位距离上的两层流体间的相对速度成比例,比例系数 μ \mu μ称为流体的动力粘度(单位是 N ⋅ s / m 2 N\cdot s/m^2 N⋅s/m2)。若 μ \mu μ为常数,则称该类流体为牛顿流体。否则称为非牛顿流体。
对于牛顿流体,通常用
ν
\nu
ν来代替
μ
\mu
μ:
一般来说,牛顿流体的粘性比较小,对应的液体是小分子液体。
理想流体与粘性流体
**粘性(viscosity)**是流体内部发生相对运动而引起的内部相互作用。流体有抵抗两层流体间相对滑动速度,或普遍来说抵抗变形的性质,称为粘性。
当流体的粘性较小,运动的相对速度也不大时,所产生的粘性应力比起其他类型的力(如惯性力)可忽略不计,此时称这种流体为无粘流体。
应力
应力的单位是帕斯卡(Pa),即
N
/
m
2
N/m^2
N/m2。正应力
σ
=
d
F
d
A
\sigma=\frac{dF}{dA}
σ=dAdF,表示材料内部单位面积上的应力。通俗地说,应力就是物体在受到外界作用时物体各部分的材料贡献的内力。如图: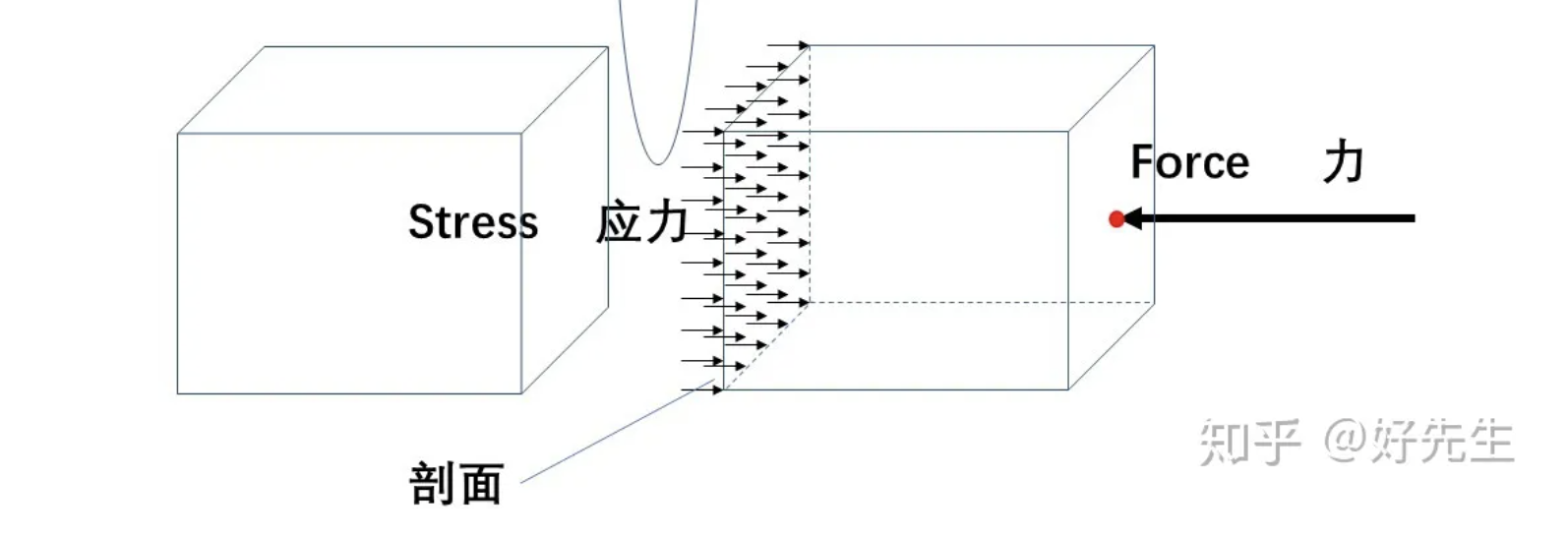
所以1Pa其实就是指1平方米的面积上受到了1N的力。当材料不均匀的时候,应力也是不均匀的
切应力也称为剪应力,指的是平行于截面的力: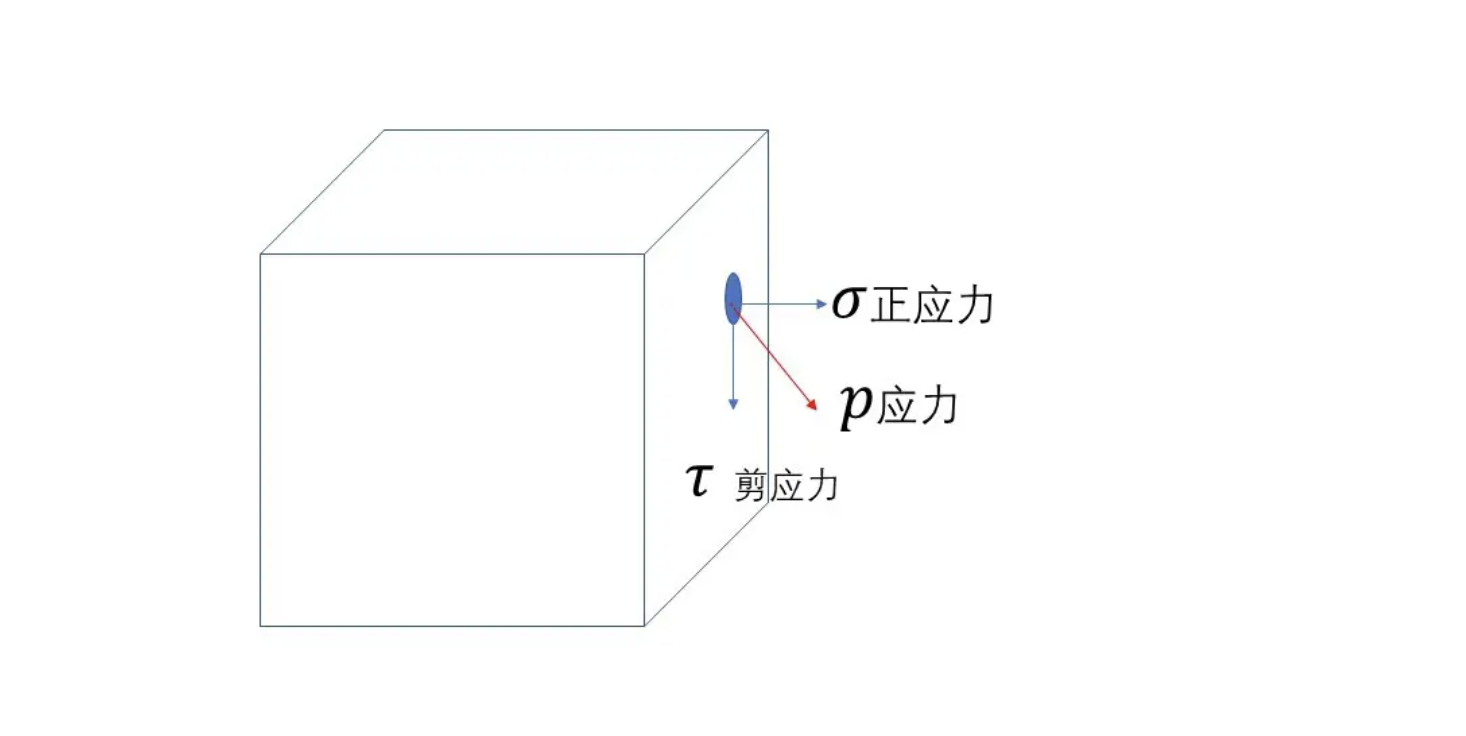
流体扩散
当流体混合物中存在着组元的浓度差时,浓度高的地方将向浓度低的地方输送该组元的物质,这种现象称为扩散.
可压流体与不可压流体
当密度 ρ \rho ρ为常数时,流体为不可压流体;当密度不为常数的时候,就是可压流体。最经典的,水就是不可压流体,空气就是可压流体.
定常与非定常流动
当流动的物理量不随时间变化,为定常流动;
当流动的物理量随时间变化,为非定常流动.
层流与湍流
层流是指流体在流动过程中两层之间没有相互混掺;而湍流是指流体不是出于分层流动状态。一般来说,湍流是普遍的,层流属于个别情况.
雷诺数: R e = u d ν Re=\frac{ud}{\nu} Re=νud,其中u是液体流速, ν \nu ν是运动粘度,d为管径.对于圆管内流动,当 R e ≤ 2300 Re\leq 2300 Re≤2300时,管流一定是层流;Re≥8000~12000 时,管流一定为湍流;当2300<Re<8000,流动处于层流与湍流间的过渡区.
物理边界条件
-
无滑移条件:紧挨物面的气流与物面之间的相对速度为0,如果流动流经固定的物面,那么应该有
u = v = w = 0 在物面(对于粘性流动) u=v=w=0\,\ 在物面(对于粘性流动) u=v=w=0 在物面(对于粘性流动) -
温度无滑移条件:记物面材料的温度为 T w T_w Tw(壁面温度),则直接与物面接触的气流的温度也是 T w T_w Tw。在壁面温度已知的给定问题中,边界条件为:
T = T w 在物面 T=T_w\,\ 在物面 T=Tw 在物面 -
若壁面温度未知,例如,由于有热流传入物面或是由物面传给气流,壁面温度是随时间变化的函数,设 q w ˙ \dot{q_w} qw˙为传给物面的瞬时热流,则由傅立叶定律:
q w ˙ = − ( k ∂ t ∂ n ) \dot{q_w}=-\left(k\frac{\partial t}{\partial n}\right) qw˙=−(k∂n∂t)
知对于非定常热流问题,边界条件是:
( ∂ T ∂ n ) w = − q w ˙ k 在物面 \left(\frac{\partial T}{\partial n}\right)_w=-\frac{\dot{q_w}}{k} \,\ 在物面 (∂n∂T)w=−kqw˙ 在物面 -
绝热壁边界条件:若壁面温度达到这样一种程度,使得不再有热流传给物面,这个壁面温度定义为绝热壁面温度。对于绝热壁,边界条件是:
( ∂ T ∂ n ) w = 0 在物面 \left(\frac{\partial T}{\partial n}\right)_w=0\,\ 在物面 (∂n∂T)w=0 在物面 -
对于**无粘流动,**唯一的边界条件是:
V ⋅ n = 0 在物面 V\cdot n=0\,\ 在物面 V⋅n=0 在物面
也就是垂直于物面的速度分量为0,也就是说物面上的流动与物面相切.
流体力学的控制方程
首先由物理学原理:质量守恒、牛顿第二定律、能量守恒分别得到连续性方程、动量方程(NS方程)、能量方程,统称为NS方程组。这是一个有5个方程和6个未知数的方程组。
然后加入状态方程(也称为热状态方程): p = ρ R T p=\rho RT p=ρRT,其中R是普适气体常数。但是这同时引入了第七个未知量,即温度T。
最后再加入一个方程,如 e = e ( T , p ) e=e(T,p) e=e(T,p),特殊的是 e = c v T e=c_vT e=cvT,其中 c v c_v cv是比定容热容,这个方程有时称为量热状态方程。
从而我们可以得到一个七个方程七个未知数的方程组。
边界层
雷诺数足够高的时候,会出现很薄的边界层效应,在边界层内有粘性力,在边界层外无粘性力;但是如果雷诺数很低的时候,粘性效应会影响整个区域。
理想气体
如果气体分子本身的体积和分子之间的作用力可以忽略,这种气体就称为完全气体,其状态可以用下式来表示:
p
=
ρ
R
0
M
T
p=\rho\frac{R_0}{M}T
p=ρMR0T
其中,
R
0
=
8.314
J
/
(
m
o
l
⋅
K
)
R_0=8.314J/(mol\cdot K)
R0=8.314J/(mol⋅K)是理想气体常数,M是气体的摩尔质量。
拉格朗日方法和欧拉方法
拉格朗日方法研究的目标是质点,研究什么物体的受力就着眼于这个物体,一般描述运动是:在t时刻,质点A得速度为····;
欧拉方法研究的目标不是质点,而是发生流体运动的空间,描述运动是:在t时刻,A点处流体质点的速度为····
拉格朗日坐标中描述导数是:加速度 a ⃗ = d 2 r ⃗ d t 2 \vec{a}=\frac{d^2\vec{r}}{dt^2} a=dt2d2r,但是欧拉坐标中是物质导数 a ⃗ = ∂ V ⃗ ∂ t + ( V ⃗ ⋅ ∇ ) V ⃗ \vec{a}=\frac{\partial \vec{V}}{\partial t}+(\vec{V}\cdot\nabla)\vec{V} a=∂t∂V+(V⋅∇)V.
超音速与亚音速
超音速与亚音速是描述流体速度相对于声速的一种方式.
马赫数的定义如下:
M
=
V
a
M = \frac{V}{a}
M=aV
其中,V是流体的速度,a是流体中的声速.
**亚音速:**当马赫数M<1时,流体速度低于声速。亚音速流动不会出现激波;
**音速:**当马赫数接近1时,在这一速度范围内,流动中可能会同时存在亚音速区和超音速区,可能出现局部激波;
**超音速:**当马赫数>1时,流体速度超过声速。超音速流动中会出现激波,流动特征(压缩和膨胀效应)显著;
**高超音速:**当马赫数>5时,流体被称为高超音速。
焓
焓用来描述系统的总能量,焓的定义为系统的内能与系统所占有体积的压力积之和:
H
=
U
+
P
V
H=U+PV
H=U+PV
其中,H是焓(单位:焦耳);U是系统的内能(J);P是系统的压力(Pa);V是系统的体积(
m
3
m^3
m3)
在等压过程中,焓变化等于系统吸收或释放的热量;
比焓
比焓是焓的质量比值,定义为:
h
=
H
m
h=\frac{H}{m}
h=mH
其中,h是比焓(J/kg);H是总焓(J);m是质量。
理想气体的比焓可以用定压比热容和温度来表示:
h
=
c
p
T
h=c_pT
h=cpT
总焓
总焓用来描述流体的能量状态,它是流体的焓和动能之和:
h
0
=
h
+
V
2
2
h_0=h+\frac{V^2}{2}
h0=h+2V2
其中,
h
0
是总焓
h_0是总焓
h0是总焓;h是静焓,即流体的焓,表示为
h
=
c
p
T
h=c_pT
h=cpT;V是流体的速度。
熵解
熵解在处理非线性双曲型守恒型方程(如欧拉方程)。熵解的引入是为了应对经典解可能不唯一或者不存在的情况,从而保证物理上的合理性。
守恒律方程写为: ∂ u ∂ t + ∇ ⋅ f ( u ) = 0 \frac{∂u}{∂t}+∇⋅f(u)=0 ∂t∂u+∇⋅f(u)=0,其中u是保守变量,f(u)是流通量向量。
在非线性守恒律方程中,解可以产生激波,即解在某些点处发生不连续,这些不连续点会导致方程的经典解(即处处连续并可微的解)可能不唯一,或者在某些情况下根本不存在。为了选择物理上合理的解,我们引入了熵条件。
熵解排除了不合理的激波和其他不连续现象。
Riemann问题和Sod问题
Riemann问题是一类具有分段常数初始条件的保守型双曲偏微分方程,即Riemann问题的初始条件通常表现为在某个界面上有不连续性
Sod问题是一个具体的Riemann问题,初始条件定义如下:
左侧区域(高压区):
密度 ( r h o L = 1.0 rho_L = 1.0 rhoL=1.0) - 速度 ( u L = 0.0 u_L = 0.0 uL=0.0) - 压力( P L = 1.0 P_L = 1.0 PL=1.0)
右侧区域(低压区):
密度 ( r h o R = 0.125 rho_R = 0.125 rhoR=0.125) - 速度 ( u R = 0.0 u_R = 0.0 uR=0.0) - 压力 ( P R = 0.1 P_R = 0.1 PR=0.1)