乘法逆元：

在这里插入图片描述
因为涉及到除法，所以取余这个操作就错误。
所以如果我们要求（a/b)%mod，我们可以假设
(a/b)%mod = a*c%mod
那么c就是b的逆元。

怎么求逆元呢，其实有很多方法，这里我先学习了两种比较常用的方法。

逆元的定义

给定正整数a，p，如果有 $ax \equiv 1 : (mod ; p)$ ，且a与p互质，则称x的最小正整数解为a模p的逆元。

方法一：拓展欧几里得算法

不要求模p为质数，所以我一般会用这种方法

欧几里得算法就是辗转相除法，一般用来求最大公约数
在理解拓展欧几里得算法之间先要理解一个裴属定理：
ax+by=gcd(a , b)
也就是说如果a、b是整数，那么一定存在整数x、y使得ax+by=gcd(a,b)。
换句话说，如果ax+by=m有解，那么m一定是gcd(a,b)的若干倍

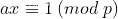在这里插入图片描述有解的条件是gcd(a, p) = 1，即a、p互质，所以根据扩展欧几里得原理，就把问题等价于求解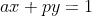
例：求6对于10^9+7的逆元

注意在递归中永远都是先得到上一层的结果状态

import java.util.Scanner;
public class Main {
	 static long x = 0;
	 static long y = 0;
	public static void main(String[] args) {
		new Main().solve();
	}
	void solve() {
		long mod = 1000000007;
		Scanner sc = new Scanner(System.in);
//		long n = sc.nextInt();
		long res=0;
		System.out.println(mod_inverse(6, mod));
		sc.close();
	}
	

	void extend_gcd(long a, long b){
	    if(b == 0){
	        x = 1;
	        y = 0;
	        return;
	    }
	    extend_gcd(b, a % b);
	    long tmp = x;
	    x = y;
	    y = tmp - (a / b) * y;
	}
	long mod_inverse(long a, long mod){
	    extend_gcd(a, mod);
	    return (x % mod + mod) % mod;
	}

}

方法二：费马小定理

要求p必须是质数
费马小定理：
在这里插入图片描述
然后
如果p过大的话我们一般会用快速幂来解决
例：

import java.util.Scanner;
public class Main {
	 static long x = 0;
	 static long y = 0;
	 static long inv6 = 166666668; 
	public static void main(String[] args) {
		new Main().solve();
	}
	void solve() {
		long mod = 1000000007;
		Scanner sc = new Scanner(System.in);
//		long n = sc.nextInt();
		System.out.println(fermat(6, mod));
		sc.close();
	}

	long qmi(long a, long b, long mod){
	    long res = 1;
	    while(b!=0){
	        if((b & 1)==1) res = res * a % mod;
	        a = a * a % mod;
	        b >>= 1;
	    }
	    return res;
	}
	long fermat(long a, long mod){
	    return qmi(a, mod - 2, mod);
	}
}

数论分块：

数论跟我真的不熟，感觉它不想让我认识

这个是在求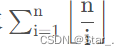在这里插入图片描述
的时候一个办法

我们先打表理解一下，
若现在n为20，然后结果为下图（偷下懒，图借鉴大佬的）
在这里插入图片描述
我们可以看出来，有很多重复的值，那么我们可不可以从头开始看看当前值重复了几次然后相乘再往后找下一个值重复了几次然后相乘直到最后一个。
假设我们的左端点为l,那么右端点就为 n/(n/l)
重复次数即为（r-l+1），当前值为 n/l （其实n/r也一样，因为要向下取整）

所以得出结论

ans = 0;
for(int l = 1, r; l <= n; l = r + 1)
{
    r = n / (n / l);
    ans += n / l * (r - l + 1);
}

其实还有很多变式，可以看看这两篇博客
数论分块总结
数学–数论–整除分块（巨TM详细，学不会，你来打我）

平方和公式：

平方和公式：1²+2²+3²+…+n²=n(n+1)(2n+1)/6.

（a-b）³＝a³－3a²b＋3ab²-b³

1³⁺²3+.+n³⁼ⁿ2(n+1)^{2/4=[n(n+1)/2]}2

（记一下以后可能有大用）

其实这些都是一道题总结的知识

因数平方和
题目描述
记 f(x) 为 x 的所有因数的平方的和。例如：f(12) = 12 + 22 + 32 + 42 + 62 + 122。

定义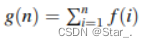
给定 n, 求 g(n) 除以 109 + 7 的余数。

输入格式
输入一行包含一个正整数 n。
输出格式
输出一个整数表示答案 g(n) 除以 109 + 7 的余数。
样例输入
100000
样例输出
680584257

思路：一开始知道两重循环暴力会超时，然后就是我之前不会的数论了，
从1到n,i作为因子的次数为n/i，
所以g(n)还可以写成
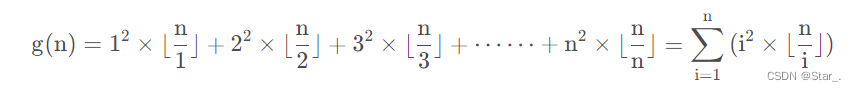
在这里插入图片描述

又因为n/i向下取整，所以必定有若干i使得n/i等于同一个值，所以就用到了数论分块
例如下方
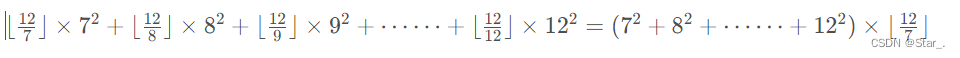
在这里插入图片描述
所以我们从1到n开始循环，计算等于n/l的数有几个，通过n/(n/l)找出最右端r，然后计算1到r的平方和再减去最左端之前的平方和就是当前重复的值的计算总和，然后再往后计算。
再计算平方和的时候肯定会用到平方和公式，然后因为要取余，平方和公式中要除以6,不能直接取余，所以我们要计算6对于模mod的逆元来代替除以6。

ac代码：

import java.util.Scanner;
public class Main {
	 static long x = 0;
	 static long y = 0;
	 static long inv6 = 166666668; 
	public static void main(String[] args) {
		new Main().solve();
	}
	void solve() {
		long mod = 1000000007;
		Scanner sc = new Scanner(System.in);
		long n = sc.nextInt();
		long res=0;
		long sum=0;
		long temp=0;
		long l=1;
		long r;
		while(l<=n) {
			r = n/(n/l);
			temp = sum;
			sum = r*(r+1)%mod*(2*r+1)%mod*inv6%mod;
			long v = (sum-temp+mod)%mod;
			res = (res+(n/l)%mod*v%mod)%mod;
			l= r+1;
		}
		System.out.println(res);
		sc.close();
	}
	
	void extend_gcd(long a, long b){
	    if(b == 0){
	        x = 1;
	        y = 0;
	        return;
	    }
	    extend_gcd(b, a % b);
	    long tmp = x;
	    x = y;
	    y = tmp - (a / b) * y;
	}
	long mod_inverse(long a, long mod){
	    extend_gcd(a, mod);
	    return (x % mod + mod) % mod;
	}
}