YoloV8改进策略：Block篇|即插即用|StarNet，重写星操作，使用Block改进YoloV8（全网首发）

摘要

本文主要集中在介绍和分析一种新兴的学习范式——星操作（Star Operation），这是一种通过元素级乘法融合不同子空间特征的方法，通过元素级乘法（类似于“星”形符号的乘法操作）将不同子空间的特征进行融合，从而在多个研究领域中展现出出色的性能和效率。
在这里插入图片描述

星操作在自然语言处理（NLP）和计算机视觉（CV）等多个领域中都得到了成功应用。例如，在自然语言处理中，Monarch Mixer、Mamba、Hyena Hierarchy和GLU等模型都采用了星操作；在计算机视觉中，FocalNet、HorNet和VAN等模型也利用了星操作进行特征融合

当将星操作融入神经网络并堆叠多层时，每一层都使隐含的维度复杂度呈指数级增长。这种高效的特征融合方式使得星操作能够在紧凑的特征空间内实现近乎无限的维度，从而极大地提高了模型的表示能力和性能。

使用StarNet改进YoloV8的block，实现超赞的效果，如果你想做轻量级改进的模型，非常推荐！

论文：《Rewrite the Stars》

https://arxiv.org/pdf/2403.19967

最近的研究已经引起了人们对网络设计中“星操作”（元素级乘法）尚未开发的潜力的关注。尽管直观的解释很多，但其应用背后的基本原理仍然在很大程度上未被探索。我们的研究试图揭示星操作将输入映射到高维、非线性特征空间的能力——类似于核技巧——而无需加宽网络。我们还引入了StarNet，这是一个简单但功能强大的原型，它在紧凑的网络结构和有限的预算下展示了令人印象深刻的性能和低延迟。就像天空中的星星一样，星操作看似普通，但蕴含着巨大的潜力。我们的工作鼓励在不同任务中进一步探索，相关代码已开源在https://github.com/ma-xu/Rewrite-the-Stars。

1、引言

在过去的十年里，学习范式在不知不觉中逐渐演变。自从AlexNet[33]以来，涌现出了无数深度网络模型[4,23,32,37,49]，它们都是基于先前的模型进行构建的。尽管这些模型各具特色且有所贡献，但它们大多基于融合线性投影（即卷积层和线性层）与非线性激活函数的模块。自从[56]以来，自注意力机制在自然语言处理中占据主导地位，并随后在计算机视觉[14]中流行开来。自注意力机制最显著的特点是将特征映射到不同的空间，然后通过点积乘法构造一个注意力矩阵。然而，这种实现方式并不高效，导致注意力机制的复杂度随着标记数量的增加而呈二次方增长。

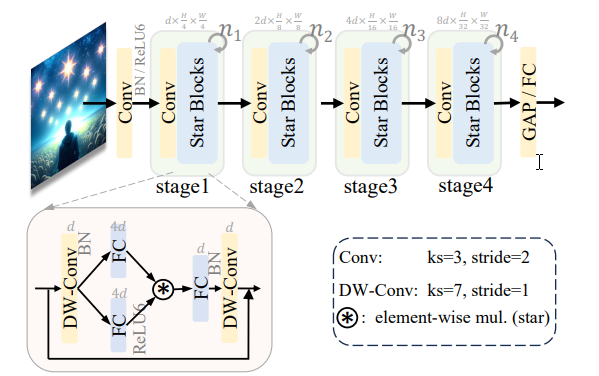
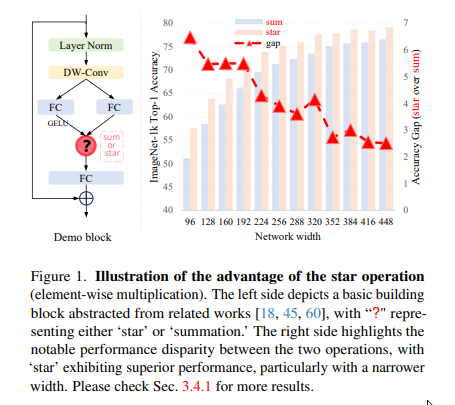
最近，一种新的学习范式逐渐受到越来越多的关注：通过元素级乘法融合不同子空间特征。为了简化表述，我们将其称为“星操作”（由于元素级乘法符号类似于星星）。星操作在多个研究领域中都展现出了出色的性能和效率，包括自然语言处理（如Monarch Mixer[16]、Mamba[17]、Hyena Hierarchy[44]、GLU[48]等）、计算机视觉（如FocalNet[60]、HorNet[45]、VAN[18]等）以及其他领域。为了说明这一点，我们为图像分类构建了一个“演示块”，如图1左侧所示。通过在主干层之后堆叠多个演示块，我们构建了一个简单的模型，名为DemoNet。在保持其他所有因素不变的情况下，我们观察到元素级乘法（星操作）在性能上始终优于求和操作，如图1右侧所示。
在这里插入图片描述

尽管星操作非常简单，但它提出了一个问题：为什么它能产生如此令人满意的结果？为了回答这个问题，已经提出了几种假设性的解释。例如，FocalNet[60]认为星操作可以作为调制或门控机制，动态地改变输入特征。HorNet[45]则认为其优势在于利用高阶特征。同时，VAN[18]和Monarch Mixer[16]都将有效性归因于卷积注意力。虽然这些初步解释提供了一些见解，但它们大多基于直觉和假设，缺乏全面分析和强有力的证据。因此，星操作背后的基本原理仍然未经检验，这给更好地理解和有效利用星操作带来了挑战。

在这项工作中，我们通过明确展示星操作具有将输入映射到极高维、非线性特征空间的能力，解释了星操作强大的表示能力。我们不依赖于直观或假设性的高级解释，而是深入探究了星操作的细节。通过重写和重新表述星操作，我们发现这个看似简单的操作可以生成一个新的特征空间，该空间包含大约 $\left(\frac{d}{\sqrt{2}}\right)^{2}$ 个线性独立的维度，具体细节见第3.1节。星操作实现这种非线性高维的方式与增加网络宽度（即通道数）的传统神经网络不同。相反，星操作类似于跨不同通道进行特征对乘的核函数，尤其是多项式核函数[25, 47]。当将星操作融入神经网络并堆叠多层时，每一层都使隐含的维度复杂度呈指数级增长。仅通过几层，星操作就能够在紧凑的特征空间内实现近乎无限的维度，具体细节见第3.2节。在紧凑的特征空间内操作同时受益于隐含的高维度，这就是星操作所展现的独特魅力所在。

基于上述见解，我们推断星操作可能天生就更适合高效、紧凑的网络，而不是传统使用的大型模型。为了验证这一点，我们介绍了一个概念验证的高效网络，名为StarNet，其特点是简洁和高效。StarNet的详细架构如图3所示。StarNet非常直观，没有复杂的设计和精细调整的超参数。在设计理念上，StarNet明显不同于现有网络，如表1所示。利用星操作的有效性，我们的StarNet甚至可以超越各种精心设计的高效模型，如MobileNetv3[27]、EdgeViT[42]、FasterNet[6]等。例如，我们的StarNet-S4在ImageNet- $1\mathrm{~K}$ 验证集上的top-1准确率比EdgeViT-XS高出 $0.9\%$ ，同时在iPhone 13和CPU上运行速度快 $3$ 倍，在GPU上快 $2$ 倍。这些结果不仅从经验上验证了我们关于星操作的见解，还强调了它在现实世界应用中的实际价值。

我们简要总结和强调本工作的主要贡献如下：

首先，我们证明了星操作的有效性，如图1所示。我们揭示了星操作具有将特征投影到极高维隐式特征空间的能力，类似于多项式核函数，具体细节见第3节。
我们通过实证结果（参考图1、表2和表3等）、理论探索（在第3节）和可视化表示（见图2）验证了我们的分析。
受我们分析的启发，我们识别了星操作在高效网络领域的实用性，并提出了一个概念验证模型，即StarNet。值得注意的是，StarNet在不需要复杂设计或精心选择的超参数的情况下，取得了令人瞩目的性能，超越了众多高效设计。
值得注意的是，基于星操作存在许多尚未探索的可能性，例如无激活的学习和在隐式维度内细化操作。我们设想，我们的分析可以作为一个指导框架，引导研究人员避免随意的网络设计尝试。

2、相关工作

神经网络中的逐元素乘法。最近的研究表明，在神经网络设计中，利用逐元素乘法进行特征聚合可能是一个比求和更有效的选择，例如FocalNet [60]、VAN [18]、Conv2Former [26]、HorNet [45]等，以及更多相关工作[35, 36, 58, 61]。为了阐明其优越性，人们提出了直观的解释，包括调制机制、高阶特征和卷积注意力的整合等。尽管已经提出了许多试探性的解释，并实现了实证上的改进，但其背后的基本原理仍然未经检验。在这项工作中，我们明确强调逐元素乘法的重要性，无论是否进行微小的架构修改。它有能力以新颖的方式将输入特征隐式地转换为极高且非线性的维度，但操作却发生在低维空间中。

高维与非线性特征变换。在传统机器学习算法[3, 20]和深度学习网络[33, 34, 49, 63]中，包含高维和非线性特征都至关重要。这种必要性源于现实世界数据的复杂性以及模型固有的表示这种复杂性的能力。然而，重要的是要认识到这两种方法从不同的角度实现了这一目标。在深度学习时代，我们通常首先通过线性投影将低维特征转换到高维空间，然后使用激活函数（如ReLU、GELU等）引入非线性。相比之下，在传统机器学习算法中，我们可以使用核技巧[10, 47]同时实现高维和非线性。例如，多项式核函数 $k\left(x_{1}, x_{2}\right)=\left(\gamma x_{1} \cdot x_{2}+c\right)^{d}$ 可以将输入特征 $x_{1}, x_{2} \in \mathbb{R}^{n}$ 投影到一个 $n+1)^{d}$ 维的高维非线性特征空间；高斯核函数 $k\left(x_{1}, x_{2}\right)=\exp \left(-\left\|x_{1}\right\|^{2}\right) \exp \left(-\left\|x_{2}\right\|^{2}\right) \sum_{i=0}^{+\infty} \frac{\left(2 x_{1}^{\top} x_{2}\right)^{i}}{i!}$ 可以通过泰勒展开得到无限维的特征空间。相比之下，我们可以看到经典的机器学习核方法和神经网络在实现和理解高维与非线性特征上存在差异。在这项工作中，我们证明了星操作可以在低维输入内获得高维和非线性特征空间，类似于核技巧的原理。图2中的一个简单可视化实验进一步说明了星操作与多项式核函数之间的联系。
在这里插入图片描述

高效网络。高效网络致力于在计算复杂性和性能之间找到理想的平衡。近年来，为了增强网络的效率，引入了许多创新的概念。这些概念包括深度卷积[28, 46]、特征重用[6,19]和重参数化[55]等。表1中提供了一个全面的总结。与所有先前的方法形成鲜明对比的是，我们展示了星操作可以作为高效网络的一种新颖方法。它具有独特的能力，可以在低维空间中执行计算时隐式地考虑极高维特征。这一显著优点使得星操作在高效网络领域中与其他技术区别开来，并使其特别适合用于高效网络设计。通过星操作，我们展示了一个简单的网络可以轻松地超越经过精心设计的复杂网络。

在这里插入图片描述

3、重写星操作

我们首先通过重写星操作来明确展示其实现极高维度的能力。接着，我们将展示在多层网络后，星操作可以显著增加隐式维度到近乎无限维。之后将进行相关讨论。

3.1、单层中的星操作

在神经网络的单层中，星操作通常被写为 $\left(\mathrm{W}_{1}^{\mathrm{T}} \mathrm{X}+\mathrm{B}_{1}\right) *\left(\mathrm{~W}_{2}^{\mathrm{T}} \mathrm{X}+\mathrm{B}_{2}\right)$ ，这表示通过逐元素乘法融合两个线性变换的特征。为了方便起见，我们将权重矩阵和偏置合并为一个实体，记作 $\mathrm{W}=\left[\begin{array}{l}\mathrm{W} \\ \mathrm{B}\end{array}\right]$ ，同样地， $\mathrm{X}=\left[\begin{array}{c}\mathrm{X} \\ 1\end{array}\right]$ ，从而简化星操作为 $\left(\mathrm{W}_{1}^{\mathrm{T}} \mathrm{X}\right) *\left(\mathrm{~W}_{2}^{\mathrm{T}} \mathrm{X}\right)$ 。为了简化分析，我们关注涉及一个输出通道变换和单元素输入的情况。具体来说，我们定义 $w_{1}, w_{2}, x \in \mathbb{R}^{(d+1) \times 1}$ ，其中 $d$ 是输入通道数。它可以很容易地扩展到多个输出通道 $\mathrm{W}_{1}, \mathrm{~W}_{2} \in \mathbb{R}^{(d+1) \times\left(d^{\prime}+1\right)}$ 和处理多个特征元素，其中 $\mathrm{X} \in \mathbb{R}^{(d+1) \times n}$ 。

一般来说，我们可以将星操作重写为：
$\begin{aligned} & w_{1}^{\mathrm{T}} x * w_{2}^{\mathrm{T}} x \\ = & \left(\sum_{i=1}^{d+1} w_{1}^{i} x^{i}\right) *\left(\sum_{j=1}^{d+1} w_{2}^{j} x^{j}\right) \\ = & \sum_{i=1}^{d+1} \sum_{j=1}^{d+1} w_{1}^{i} w_{2}^{j} x^{i} x^{j} \\ = & \underbrace{\alpha_{1}^{1} x^{1}+\cdots+\alpha_{(4,5)} x^{4} x^{5}+\cdots+\alpha_{(d+1, d+1)} x^{d+1} x^{d+1}}_{(1,1)} \end{aligned}$
其中，我们使用 $i, j$ 来索引通道， $\alpha$ 是每个项的系数：

$\alpha_{(i, j)}=\left\{\begin{array}{cc} w_{1}^{i} w_{2}^{j} & \text { if } i==j, \\ w_{1}^{i} w_{2}^{j}+w_{1}^{j} w_{2}^{i} & \text { if } i!=j . \end{array}\right.$

在将式1中的星操作重写后，我们可以将其扩展为一个由 $\frac{(d+2)(d+1)}{2}$ 个不同项组成的组合，如式4所示。值得注意的是，除了 $\left.\alpha_{(d+1,:)} x^{d+1} x\right)$ 项外，每个项（与 $x$ ）都表现出非线性关联，表明它们是独立且隐式的维度。因此，我们使用计算效率高的星操作在 $d$ 维空间中执行计算，却能在 $\frac{(d+2)(d+1)}{2} \approx\left(\frac{d}{\sqrt{2}}\right)^{2}$ （考虑 $\gg 2$ ）隐式维特征空间中实现表示，显著放大了特征维度，而无需在单个层中增加任何额外的计算开销。值得注意的是，这一显著特性与核函数有相似的理念，我们建议读者参考[25,47]以获取更广泛和深入的见解。

3.2、扩展到多层

接下来，我们展示通过堆叠多层，我们可以以递归的方式将隐式维度几乎无限地指数增长。

考虑一个初始网络层，其宽度为 $d$ ，应用一个星操作会得到表达式 $\sum_{i=1}^{d+1} \sum_{j=1}^{d+1} w_{1}^{i} w_{2}^{j} x^{i} x^{j}$ ，如式3中所述。这导致在隐式特征空间 $\mathbb{R}\left(\frac{d}{\sqrt{2}}\right)^{2^{1}}$ 中的表示。令 $O_{l}$ 表示第 $l$ 个星操作的输出，我们得到：

$\begin{array}{l} O_{1}=\sum_{i=1}^{d+1} \sum_{j=1}^{d+1} w_{(1,1)}^{i} w_{(1,2)}^{j} x^{i} x^{j} \quad \in \mathbb{R}^{\left(\frac{d}{\sqrt{2}}\right)^{2^{1}}} \\ O_{2}=\mathrm{W}_{2,1}^{\mathrm{T}} \mathrm{O}_{1} * \mathrm{W}_{2,2}^{\mathrm{T}} \mathrm{O}_{1} \quad \in \mathbb{R}^{\left(\frac{d}{\sqrt{2}}\right)^{2^{2}}} \\ O_{3}=\mathrm{W}_{3,1}^{\mathrm{T}} \mathrm{O}_{2} * \mathrm{W}_{3,2}^{\mathrm{T}} \mathrm{O}_{2} \quad \in \mathbb{R}^{\left(\frac{d}{\sqrt{2}}\right)^{2^{3}}} \\ \text{...} \\ O_{l}=\mathrm{W}_{l, 1}^{\mathrm{T}} \mathrm{O}_{l-1} * \mathrm{W}_{l, 2}^{\mathrm{T}} \mathrm{O}_{l-1} \quad \in \mathbb{R}\left(\frac{d}{\sqrt{2}}\right)^{2^{l}} \\ \end{array}$

也就是说，通过 $l$ 层，我们可以隐式地获得一个属于 $\mathbb{R}^{\left(\frac{d}{\sqrt{2}}\right)^{2^{l}}}$ 的特征空间。例如，给定一个宽度为128的10层等宽网络，通过星操作实现的隐式特征维度数量近似为 $90^{1024}$ ，这可以合理地近似为无限维度。因此，通过堆叠多层，即使只有几层，星操作也可以以指数方式显著放大隐式维度。

3.3、特殊情况

不是所有的星操作都遵循式1中的公式，其中每个分支都经历了变换。例如，VAN[18]和SENet[30]包含了一个恒等分支，而GENet- $\theta^{-}$ [29]则在没有任何可学习变换的情况下进行操作。接下来，我们将深入探讨这些独特情况的复杂性。

情况I： $W_{1}$ 和/或 $W_{2}$ 的非线性性质。在实际场景中，大量研究（如Conv2Former、FocalNet等）通过将激活函数融入，将变换函数 $W_{1}$ 和/或 $W_{2}$ 实现为非线性的。然而，关键的一点是它们维持了通道之间的通信，如式2所示。重要的是，隐式维度的数量保持不变（大约 $\frac{d^{2}}{2}$ ），因此不会影响我们在3.1节中的分析。因此，我们可以简单地将线性变换作为示例。

情况II： $\mathbf{W}_{1}^{\mathrm{T}} \mathbf{X} * \mathbf{X}$ 。当移除变换 $W_{2}$ 时，隐式维度数量从大约 $\frac{d^{2}}{2}$ 减少到 $2 d$ 。

情况III： $\mathbf{X} * \mathbf{X}$ 。在这种情况下，星操作将特征从特征空间 $\left\{x^{1}, x^{2}, \cdots, x^{d}\right\} \in \mathbb{R}^{d}$ 转换为一个新的空间，其特征由 $\left\{x^{1} x^{1}, x^{2} x^{2}, \cdots, x^{d} x^{d}\right\} \in \mathbb{R}^{d}$ 描述。

有几个值得注意的方面需要考虑。首先，星操作及其特殊情况通常（但并非必然）与空间交互相结合，通常通过池化或卷积实现，例如VAN [18]中所展示的。这些方法中的许多都强调扩大感受野的好处，但往往忽视了隐式高维空间所带来的优势。其次，结合这些特殊情况是可行的，如Conv2Former [26]所示，它融合了情况I和情况II的特点，而GENet- $\theta^{-}$ [29]则融合了情况I和情况III的元素。最后，尽管情况II和情况III在单个层中可能不会显著增加隐式维度，但通过线性层（主要用于通道通信）和跳跃连接的使用，可以在多个层中累积实现高隐式维度。

3.4、实证研究

为了证实和验证我们的分析，我们从不同角度对星操作进行了广泛的研究。

3.4.1、星操作的实证优越性

首先，我们通过实证验证了星操作相对于简单求和操作的优越性。如图1所示，我们为此演示构建了一个同构网络，称为DemoNet。DemoNet设计简单，由一个卷积层开始，该层将输入分辨率降低了16倍，随后是一系列同质的演示块（demo blocks）用于特征提取（参考图1左侧）。在每个演示块内，我们应用星操作或求和操作来融合来自两个不同分支的特征。通过改变网络的宽度和深度，我们探索了每种操作的独特属性。DemoNet的实现细节在补充算法1中提供。

从表2和表3中，我们可以看到无论网络的深度和宽度如何，星操作始终优于求和操作。这一现象验证了星操作的有效性和优越性。此外，我们还观察到随着网络宽度的增加，星操作带来的性能提升逐渐减小。然而，在改变深度的情况下，我们并没有观察到类似的现象。这种行为的差异提供了两个关键的见解：1) 表2中星操作带来的增益逐渐减小并不是因为模型尺寸增大所致；2) 基于此，它暗示星操作本质上扩展了网络的维度，从而减少了增加网络宽度所带来的额外益处。
在这里插入图片描述

3.4.2、决策边界对比

接着，我们通过视觉分析和区分星操作和求和操作之间的差异。为此，我们在一个名为"moon"的二维玩具数据集上可视化了这两种操作的决策边界[43]。该数据集由两组呈月牙形状的二维点组成。在模型配置方面，我们从演示块中移除了归一化和卷积层。鉴于该数据集相对简单，我们将模型的宽度设置为100，深度设置为4。

图2（上排）展示了由求和操作和星操作所确定的决策边界。显然，星操作划定了一个相比求和操作更加精确和有效的决策边界。值得注意的是，观察到的决策边界之间的差异并非源于非线性，因为这两种操作都在其各自的构建块中包含了激活函数。主要的区别在于星操作能够达到极高的维度，这是我们之前详细分析过的特性。

如前所述，星操作的功能类似于核函数，特别是多项式核函数。为了证实这一点，我们还在图2（下排）中展示了使用高斯核和多项式核的SVM（使用scikit-learn包[43]实现）的决策边界。正如我们所预期的，星操作产生的决策边界与多项式核非常相似，而与高斯核显著不同。这一强有力的证据进一步证实了我们分析的正确性。

3.4.3、扩展到无激活函数的网络

激活函数是神经网络中基本且不可或缺的组件。然而，常用的激活函数如ReLU和GELU等也存在一些缺点，如“均值偏移”[4,22,24]和信息损失[46]等。从网络中排除激活函数是一个有趣且可能具有优势的概念。然而，没有激活函数，传统的神经网络将因为缺乏非线性而退化为单层网络。
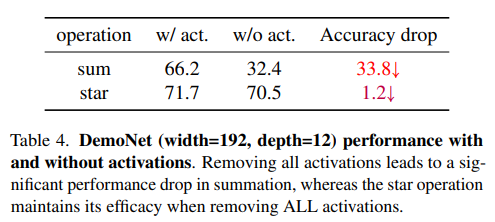
在这里插入图片描述

在本研究中，尽管我们主要关注通过星操作实现的隐式高维特征，但非线性的方面也具有重要意义。为了研究这一点，我们通过从DemoNet中移除所有激活函数来进行实验，从而创建了一个无激活函数的网络。表4中的结果非常鼓舞人心。正如预期的那样，在移除所有激活函数后，求和操作的性能显著下降，从 $66.2\%$ 下降到 $32.4\%$ 。相比之下，星操作在消除激活函数后仅受到极小的影响，准确率仅下降了 $1.2\%$ 。这一实验不仅证实了我们的理论分析，还为未来的研究开辟了广阔的道路。

3.5、开放讨论与更广泛的影响

尽管我们的分析基于简单的操作，但它为探索深度学习中的基本挑战奠定了基础。以下，我们概述了几个值得进一步研究的有趣且充满希望的研究问题，其中星操作可能会发挥关键作用。

I. 激活函数真的不可或缺吗？在我们的研究中，我们专注于星操作引入的隐式高维特性。值得注意的是，星操作也包含了非线性，这是核函数与其他线性机器学习方法的区别。我们研究中的初步实验展示了在神经网络中消除激活层的潜在可行性。

II. 星操作与自注意力和矩阵乘法有何关系？自注意力利用矩阵乘法产生 $\mathbb{R}^{n \times n}$ 中的矩阵。可以证明，自注意力中的矩阵乘法与元素乘法具有相似的属性（非线性和高维性）。值得注意的是，矩阵乘法促进了全局交互，这与元素乘法不同。然而，矩阵乘法会改变输入的形状，需要额外的操作（例如池化、另一轮矩阵乘法等）来调和张量形状，而元素乘法则避免了这种复杂性。PolyNL [2] 在这个方向上提供了初步的努力。我们的分析可能为自注意力的有效性提供新的见解，并有助于重新审视神经网络中的“动态”特征 [7,8,12]。

III. 如何优化隐式高维空间中的系数分布？传统的神经网络可以为每个通道学习一组独特的权重系数，但在星操作中，每个隐式维度的系数（类似于核函数）是固定的。例如，在多项式核函数 $k\left(x_{1}, x_{2}\right)=\left(\gamma x_{1} \cdot x_{2}+c\right)^{d}$ 中，系数分布可以通过超参数进行调整。在星操作中，尽管权重 $\mathrm{W}_{1}$ 和 $\mathrm{W}_{2}$ 是可学习的，但它们仅提供了有限的微调范围，而无法像传统神经网络那样为每个通道定制系数。这种限制可能解释了为什么极高维度只带来中等的性能提升。值得注意的是，跳跃连接似乎有助于平滑系数分布[57]，而密集连接（如DenseNet[32]中的连接）可能提供额外的益处。此外，使用指数函数可能直接映射到隐式无限维度，类似于高斯核函数。

4、概念验证：StarNet

鉴于星操作（star operation）的独特优势——它能够在低维空间中计算并产生高维特征，我们识别出它在高效网络架构领域的实用性。因此，我们引入StarNet作为概念验证模型。StarNet以极简的设计和显著减少人为干预为特点。尽管其设计简单，但StarNet展示了卓越的性能，凸显了星操作的有效性。

4.1、StarNet架构

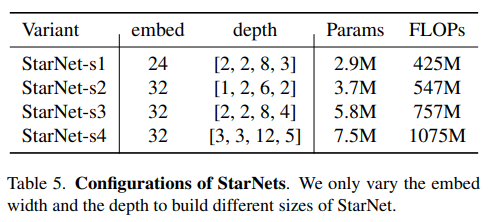
StarNet设计为四阶段的层次结构，利用卷积层进行下采样，并使用修改后的demo块进行特征提取。为了满足效率要求，我们将层归一化（Layer Normalization）替换为批归一化（Batch Normalization），并将其放置在深度卷积之后（在推理过程中可以融合）。受MobileNeXt[66]的启发，我们在每个块的末尾加入了深度卷积。通道扩展因子始终设置为4，每个阶段的网络宽度加倍。demo块中的GELU激活函数被替换为ReLU6，遵循MobileNetv2[46]的设计。StarNet的框架如图3所示。我们仅通过改变块的数量和输入嵌入通道数量来构建不同大小的StarNet，具体细节如表5所示。
在这里插入图片描述

虽然许多高级设计技术（如重新参数化、结合注意力机制、SE块等）在经验上可以增强性能，但它们也会掩盖我们的贡献。通过有意避开这些复杂的设计元素并尽量减少人为设计干预，我们强调了星操作在StarNet概念化和功能中的核心作用。
在这里插入图片描述

4.2、实验结果

我们遵循DeiT[53]的标准训练配方来确保在训练我们的StarNet模型时进行公平比较。所有模型都从头开始训练300个周期，使用AdamW优化器[39]，初始学习率为 $3 e - 3$ ，批量大小为2048。详细的训练细节在补充材料中提供。为了基准测试的目的，我们将我们的PyTorch模型转换为ONNX格式[13]，以便于在CPU（Intel Xeon CPU E5-2680 v4 @ 2.40GHz）和GPU（P100）上进行延迟评估。此外，我们使用CoreML-Tools[1]在iPhone 13上部署模型，以评估移动设备上的延迟。这些基准测试的详细设置也在补充材料中提供。
在这里插入图片描述

实验结果如表6所示。通过最小程度的人工设计，我们的StarNet能够在与其他许多最先进的高效模型相比时展现出令人鼓舞的性能。值得注意的是，StarNet在iPhone 13设备上仅用0.7秒就达到了73.5%的top-1准确率，在相同延迟下超越了MobileOne-S0 2.1%（73.5%对比71.4%）。当将模型扩展到1G FLOPs预算时，StarNet继续展现出卓越的性能，超过了MobileOne-S2 1.0%，并且比EdgeViT-XS快三倍（1.0毫秒对比3.5毫秒）的同时，还超出了其0.9%的准确率。考虑到模型设计的直接性，这种令人印象深刻的效率主要归功于星操作的基础作用。图4进一步展示了各种模型之间的延迟-准确率权衡。
在这里插入图片描述

如果我们能进一步将StarNet的性能推向更高的水平呢？我们相信，通过仔细的超参数优化，利用表1中的见解，以及应用训练增强技术（如更多的训练周期或知识蒸馏），可以对StarNet的性能进行显著的改进。然而，实现一个高性能模型并不是我们的主要目标，因为这样的增强可能会掩盖星操作的核心贡献。我们在此留下了工程工作。

4.3、更多消融研究

替换星操作。星操作被我们识别为模型高性能的唯一贡献者。为了实证验证这一断言，我们在实现中系统性地将星操作替换为求和操作。具体来说，这涉及到在模型架构中将’*‘运算符替换为’+'运算符。

结果如表7所示。移除所有星操作后，性能出现了显著的下降，观察到准确率下降了3.1%。有趣的是，星操作对性能的影响在模型的第一和第二阶段似乎是最小的。这一观察是合乎逻辑的。由于宽度非常窄，ReLU6激活导致一些特征变为零。在星操作的背景下，这会导致其隐式高维空间中的许多维度也变为零，从而限制了其全部潜力。然而，在最后两个阶段（更多通道），星操作的贡献变得更加显著，分别带来了1.6%和1.6%的改进。表7的最后三行也验证了我们的分析。

星操作对延迟的影响

理论上，乘法操作（如本研究中的星操作）相对于更简单的求和操作具有更高的计算复杂度，这在一些相关工作中得到了指示[5,15]。然而，实际的延迟结果可能并不总是与理论预测一致。我们进行了基准测试，以比较将所有星操作替换为求和操作的延迟，结果详见表8。从表中，我们观察到延迟的影响取决于硬件。在实践中，相对于求和操作，星操作在GPU和iPhone设备上并没有导致任何额外的延迟。然而，在CPU上，求和操作略优于星操作（例如，StarNet-S4的8.4毫秒对比9.4毫秒）。鉴于显著的性能差距，CPU上的这种微小延迟开销可以忽略不计。
在这里插入图片描述

激活函数位置的研究

我们对网络块内激活函数（ReLU6）的放置进行了全面分析。为了清晰起见，使用x_{1}和x_{2}来表示两个分支的输出，以StarNet-S4作为演示模型。

在这里，我们研究了在StarNet中实现激活函数的四种方法：1) 不使用激活函数，2) 两个分支都激活，3) 在星操作后激活，4) 仅激活一个分支，这是我们的默认做法。如表9所示的结果表明，仅激活一个分支可获得最高的准确率，达到78.4%。令人鼓舞的是，从StarNet中完全移除激活函数（除了主干层中的一个）仅导致准确率下降了2.8%，降至75.6%，这一性能仍然与表6中的一些强大基线相竞争。这些发现与表4一致，强调了无激活网络的潜力。
在这里插入图片描述

关于带有星操作的块设计的研究。在StarNet中，星操作通常被实现为 $\operatorname{act}\left(\mathrm{W}_{1}^{\mathrm{T}} \mathrm{X}\right) *\left(\mathrm{~W}_{2}^{\mathrm{T}} \mathrm{X}\right)$ ，如第3.1节所述。这种标准方法使得StarNet-S4能够达到84.4%的准确率。然而，也存在其他可能的实现方式。我们尝试了一种变体： $\left(\mathrm{W}_{2}^{\mathrm{T}} \operatorname{act}\left(\mathrm{W}_{1}^{\mathrm{T}} \mathrm{X}\right)\right) * \mathrm{X}$ ，其中 $\mathrm{W}_{1} \in \mathbb{R}^{d \times d^{\prime}}$ 用于扩展宽度，而 $\mathrm{W}_{2} \in \mathbb{R}^{d^{\prime} \times d}$ 则将其恢复回 $d$ 。这种调整仅对一个分支进行变换，而另一个分支保持不变。我们改变 $d^{\prime}$ 的值以确保与StarNet-S4相同的计算复杂度。这样做后，性能从78.4%下降到74.4%。虽然一个更好和更仔细的设计可能会缩小这种性能差距（见补充材料），但准确率的显著差异强调了我们在利用星操作能力方面初始实现的有效性，并强调了在星操作中变换两个分支的关键重要性。

5、结论

在本研究中，我们深入探讨了星操作的复杂细节，超越了先前研究中直观和合理的解释。我们重新定义了星操作，揭示了其强大的表示能力来源于隐式的高维空间。在很多方面，星操作都反映了多项式核函数的行为。我们的分析通过实证、理论和视觉方法得到了严格验证。我们的结果是数学和理论上的坚实基础，与我们提出的分析相一致。基于这一基础，我们将星操作置于高效网络设计的领域中，并引入了StarNet这一简单的原型网络。StarNet在不依赖复杂设计或精心选择的超参数的情况下，取得了令人印象深刻的性能，这证明了星操作的有效性。此外，我们对星操作的探索开辟了许多潜在的研究方向，正如我们之前所讨论的。

补充材料

本补充文档详细阐述了在图1、表 3和表2中展示的DemoNet的实现细节。同时，它也涵盖了用于可视化决策边界的简单网络（如图2所示）的实现，以及我们提出的StarNet在表 6中的实现（具体细节可以在A节中找到）。此外，我们在B节中提供了决策边界可视化的更详细视图。C节深入探讨了我们对超紧凑模型的探索性研究。D节展示了激活分析。最后，E节讨论了块设计的详细分析。

A、实现细节

A.1、模型架构

DemoNet 在我们的等向DemoNet中，如图1、表3和表2所示，详细的实现已在Algorithm 1中提供。我们调整深度或宽度值以便于在上述图表和表格中展示的实验。
在这里插入图片描述

DemoNet用于2D点对于图2中展示的2D点示例，我们进一步简化了DemoNet的结构。在这种适配中，原始DemoNet中的所有卷积层都已被移除。此外，我们将GELU激活函数替换为ReLU以简化架构。这个简化版DemoNet的详细信息在Algorithm 2中进行了概述。

在这里插入图片描述

StarNet 为了便于复现，我们在补充材料中包含了一个专门用于我们StarNet的单独文件。有关其架构的详细信息也可在4.1节中找到。

A.2、训练方案

接下来，我们为每个实验提供详细的训练方案。

DemoNet 对于所有DemoNet变体，我们使用了一致且标准的训练方案。尽管公认的是，专门化和精细调整的训练方案可能更适合不同模型大小，并可能产生更好的性能，如在DemoNet（宽度=96，深度=12）（大约1.26M参数）和DemoNet（宽度=288，深度=12）（大约9.68M参数）的情况下，但使用DemoNet获得卓越性能并不是本工作的主要目标。我们的目标是在各种DemoNet变体之间提供公平的比较；因此，相同的训练方案应用于所有变体。DemoNet的这种训练方案的详细信息如表10所示。
在这里插入图片描述

DemoNet用于2D点 鉴于2D点的固有简单性，我们消除了所有数据增强过程，并减少了训练周期数。这个简化流程的具体训练方案详见表11。
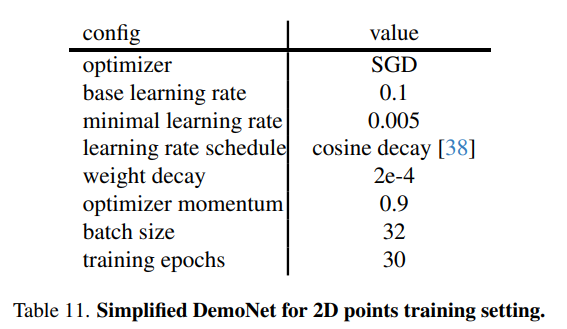
在这里插入图片描述

StarNet 由于其模型尺寸小且架构设计直观，StarNet在训练正则化时需要较少的增强。重要的是，我们选择不使用常用的指数移动平均（EMA）和可学习的层尺度技术[54]。虽然这些方法可能会提高性能，但它们可能会掩盖我们工作的独特贡献。各种StarNet模型的详细训练方案如表12所示。

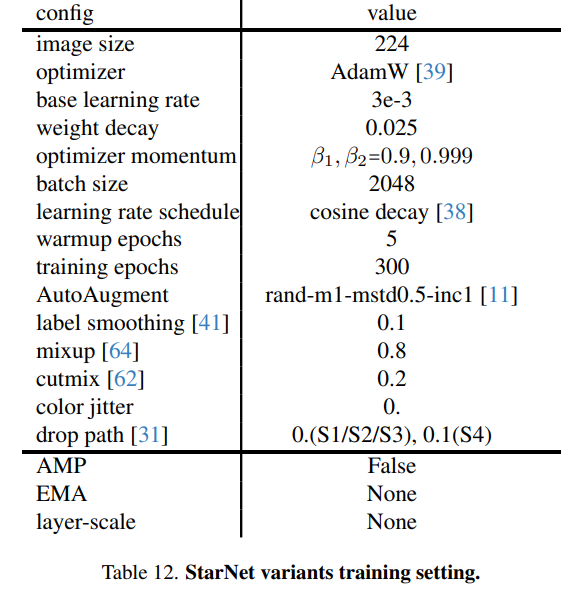
在这里插入图片描述

A.3、延迟基准测试设置

表6中列出的所有模型都已从PyTorch代码转换为ONNX格式[13]，以便在不同硬件上进行延迟评估：CPU（Intel Xeon CPU E5 2680 v4 @ 2.40 GHz）和GPU（P100）。我们进行了基准测试，其中批次大小为1，以模拟真实世界的应用场景。基准测试包括50次迭代的预热阶段，随后计算500次迭代的平均延迟。重要的是要注意，所有模型都在同一设备上进行了基准测试，以确保比较的公平性。对于CPU基准测试，我们利用4个线程来优化性能。在GPU评估的情况下，我们将StarNet中的逐点卷积层适应为线性层，并加入了置换操作。这一修改是基于观察到稍微更快的推理速度而做出的。重要的是要注意，从数学上讲，逐点卷积层等价于线性层。因此，这一变化不会导致我们StarNet的性能差异或架构变动。

得益于MobileOne[55]，我们利用了他们的开源iOS基准测试应用程序对所有CoreML模型进行了测试。我们的延迟基准测试设置遵循MobileOne中使用的设置，唯一的区别是我们在测试中包含了更多的模型。我们观察到，iOS基准测试的初次运行总是会产生稍微快一些的结果。为了考虑这一点，每个模型都运行三次，我们报告最后一次运行的延迟。尽管在iPhone上进行测试时存在微小的延迟变化，但这些差异（通常小于 $\mathrm{~ms}$ ）不会影响我们的分析。

B、决策边界可视化

我们为决策边界可视化提供了更多的分析，如图2所示。

首先，作为对图2的补充，我们展示了更全面的结果。由于不同测试中的随机性，决策边界可能会表现出显著的差异。为了说明这一点，我们在图5中展示了另外四次运行（没有固定种子）的决策边界。如图所示，星操作不仅在表示能力上超越了求和操作，而且还展示了更大的鲁棒性，表现出最小的方差。
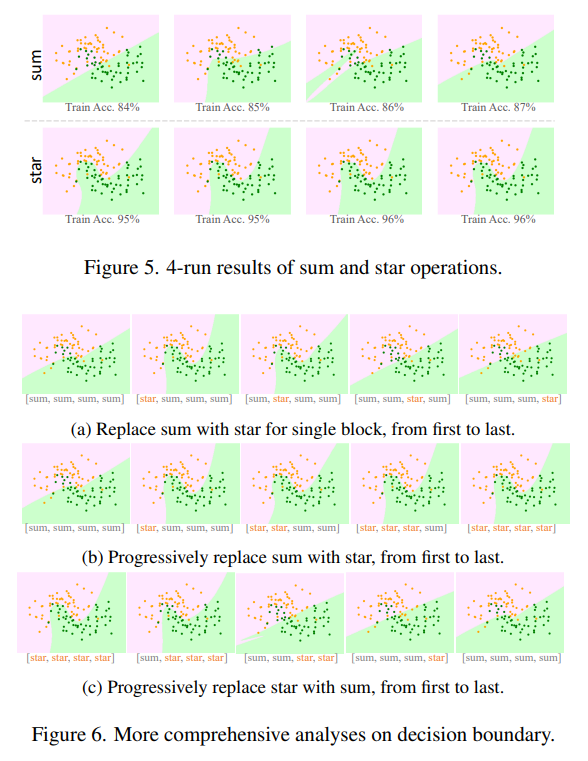
在这里插入图片描述

接下来，我们的研究扩展到了对决策边界的深入分析。考虑到网络有4个块，我们尝试将求和与星操作混合使用，以图6所示的各种组合方式进行应用。这一探索的视觉结果表明，在网络早期块中使用星操作能带来最显著的好处。
在这里插入图片描述

SVM中超参数的影响。应该注意的是，参数调整会导致不同的可视化结果，这可能会对我们的基于图2的论点构成挑战。然而，由于ploy和rbf核之间的内在差异，这种变化并不显著，如图7所示。我们基于星的网络决策边界始终与poly-SVM的决策边界相似。因此，不仅有理论证明，我们的视觉实验也坚如磐石。

C、探索极小模型

在本节中，我们探索了StarNet在极小参数（大约 $\mathrm{M}$ 、 $\mathrm{M}$ 和 $\mathrm{M}$ ）下的性能。对于这些极小变体，我们除了调整块数和基础嵌入宽度外，还进一步微调了MLP（多层感知器）的扩展比例。这些极小变体的详细配置如表13所示。

在本节中，我们深入研究了配置有极小参数数量的StarNet的性能，特别是大约 $\mathrm{M}$ 、 $\mathrm{M}$ 和 $\mathrm{M}$ 的情况。对于这些超紧凑变体，我们不仅仅调整了块数和基础嵌入宽度，还精细地微调了MLP的扩展比例。这些极小StarNet变体的具体配置在表13中详细列出。
在这里插入图片描述

表14中的结果显示，我们StarNet的超紧凑变体在性能上也很有前途。与MobileNetv2-050相比，后者经过了更长的训练周期并引入了大约 $25\%$ 的更多参数（ $\mathrm{M}$ vs. $\mathrm{M}$ ），我们的StarNet-150变体在移动设备上仍然在顶1准确率和速度上表现更好。

D、激活函数分析

D.1、移除所有激活函数的分析

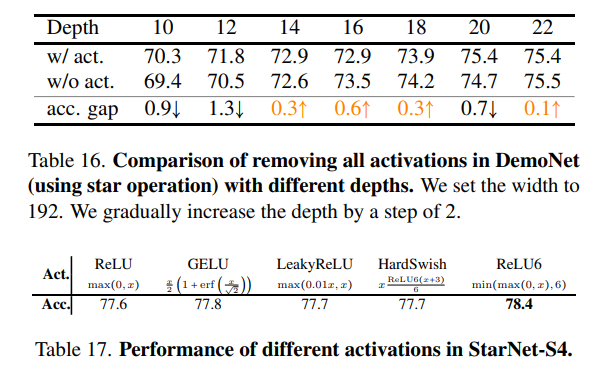
在3.5节中，我们探讨了消除所有激活函数的可能性，并在表4和表9中给出了初步结果。本节将更深入地分析移除所有激活函数的详细情况。以DemoNet作为我们的模型示例，我们在表15和表16中提供了进一步的结果。
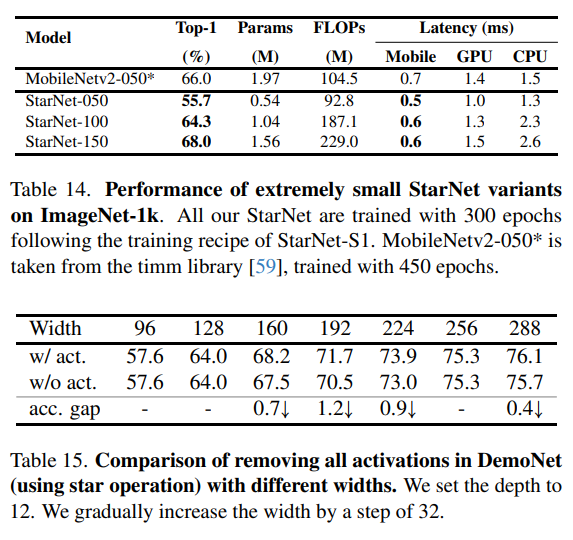
在这里插入图片描述

在大多数情况下，我们观察到从DemoNet（使用星操作）中移除所有激活函数后，性能略有下降。然而，出现了一个有趣的现象：在某些情况下，移除所有激活函数后，性能相似甚至更好。当深度值设置为14、16、18和22时，这一点尤为明显，如表16所示。这一现象表明，星操作可能本身就提供了足够的非线性，类似于通常通过激活层实现的效果。我们认为，对这一方向进行更彻底的研究可能会产生有价值的见解。

D.2、探索激活函数类型

在我们的StarNet设计中，我们采用了ReLU6激活函数，这是遵循MobileNetv2的做法。此外，我们还尝试了其他各种激活函数，并将这些探索的结果列在表17中。从经验上看，我们发现当StarNet-S4配备ReLU6激活函数时，性能最佳。

在这里插入图片描述

E、块设计的探索

我们对StarNet块的设计进行了详细的消融研究。为此，我们在StarNet中展示了五种星操作的实现方式，如图8所示。值得注意的是，Block I可以被视为星操作的标准实现，Block II和Block III可以被视为第3.3节中讨论的特殊情况II的实例化，而Block IV和Block V可以被视为特殊情况III的不同实现。这些块变体通过调整扩展比率来保持相同的参数数量和浮点运算次数（FLOPs），以确保在公平比较下具有相同的计算复杂度。我们在StarNet-S4架构的基础上测试了所有这些块变体，并将性能报告在表18中。经验上，我们发现Block I、Block IV和Block V表现出强大的性能，而Block II和Block III的性能较差。详细的结果表明，强大的性能主要来源于星操作本身，而不是特定的块设计。我们将默认的星操作（Block I）视为我们StarNet中的基本构建块。
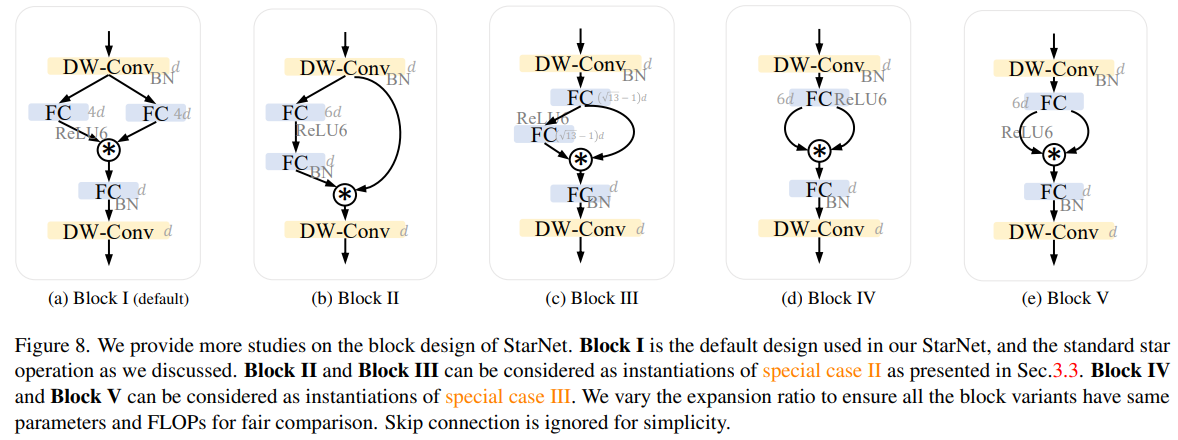
在这里插入图片描述

我们已经对StarNet块的设计进行了详细的消融研究。为此，我们探索了StarNet中星操作的五种不同实现方式，如图8所示。值得注意的是，Block I代表了星操作的标准实现。Block II和Block III是3.3节中讨论的特殊情况II的实例化，而Block IV和Block V则提供了特殊情况III的另一种实现方式。所有这些块变体都通过调整扩展比率来保持相同的参数数量和浮点运算次数（FLOPs），以确保在公平比较下具有相同的计算复杂度。这些块变体在StarNet-S4架构框架中进行了测试，其性能在表18中详细列出。经验上，Block I、Block IV和Block V表现出了强大的性能，并且性能差距很小。这些发现表明，其有效性更多地归因于星操作本身，而不是特定块的设计。因此，我们将默认的星操作（Block I）作为我们StarNet中的基础构建块。

在这里插入图片描述

F、StarNet的更多延迟分析

CPU延迟可视化。为了更好地理解概念验证模型StarNet的延迟，我们进一步在图9中绘制了CPU延迟的权衡关系。

移动设备延迟鲁棒性。在表6中，我们展示了在iPhone13手机上测试的移动设备延迟。为了测试不同模型的延迟稳定性，我们进一步在4种不同的移动设备上进行了延迟测试，包括iPhone12、iPhone12 Pro Max、iPhone 13和iPhone14。表19中的结果显示，尽管某些模型的延迟结果有所不同，但StarNet在不同手机上的推理始终表现出稳定性，这归因于其简单的设计。
在这里插入图片描述

代码

import torch
import torch.nn as nn
from timm.models.layers import DropPath, trunc_normal_
from timm.models.registry import register_model

model_urls = {
    "starnet_s1": "https://github.com/ma-xu/Rewrite-the-Stars/releases/download/checkpoints_v1/starnet_s1.pth.tar",
    "starnet_s2": "https://github.com/ma-xu/Rewrite-the-Stars/releases/download/checkpoints_v1/starnet_s2.pth.tar",
    "starnet_s3": "https://github.com/ma-xu/Rewrite-the-Stars/releases/download/checkpoints_v1/starnet_s3.pth.tar",
    "starnet_s4": "https://github.com/ma-xu/Rewrite-the-Stars/releases/download/checkpoints_v1/starnet_s4.pth.tar",
}

class ConvBN(torch.nn.Sequential):
    def __init__(self, in_planes, out_planes, kernel_size=1, stride=1, padding=0, dilation=1, groups=1, with_bn=True):
        super().__init__()
        self.add_module('conv', torch.nn.Conv2d(in_planes, out_planes, kernel_size, stride, padding, dilation, groups))
        if with_bn:
            self.add_module('bn', torch.nn.BatchNorm2d(out_planes))
            torch.nn.init.constant_(self.bn.weight, 1)
            torch.nn.init.constant_(self.bn.bias, 0)


class Block(nn.Module):
    def __init__(self, dim, mlp_ratio=3, drop_path=0.):
        super().__init__()
        self.dwconv = ConvBN(dim, dim, 7, 1, (7 - 1) // 2, groups=dim, with_bn=True)
        self.f1 = ConvBN(dim, mlp_ratio * dim, 1, with_bn=False)
        self.f2 = ConvBN(dim, mlp_ratio * dim, 1, with_bn=False)
        self.g = ConvBN(mlp_ratio * dim, dim, 1, with_bn=True)
        self.dwconv2 = ConvBN(dim, dim, 7, 1, (7 - 1) // 2, groups=dim, with_bn=False)
        self.act = nn.ReLU6()
        self.drop_path = DropPath(drop_path) if drop_path > 0. else nn.Identity()

    def forward(self, x):
        input = x
        x = self.dwconv(x)
        x1, x2 = self.f1(x), self.f2(x)
        x = self.act(x1) * x2
        x = self.dwconv2(self.g(x))
        x = input + self.drop_path(x)
        return x


class StarNet(nn.Module):
    def __init__(self, base_dim=32, depths=[3, 3, 12, 5], mlp_ratio=4, drop_path_rate=0.0, num_classes=1000, **kwargs):
        super().__init__()
        self.num_classes = num_classes
        self.in_channel = 32
        # stem layer
        self.stem = nn.Sequential(ConvBN(3, self.in_channel, kernel_size=3, stride=2, padding=1), nn.ReLU6())
        dpr = [x.item() for x in torch.linspace(0, drop_path_rate, sum(depths))] # stochastic depth
        # build stages
        self.stages = nn.ModuleList()
        cur = 0
        for i_layer in range(len(depths)):
            embed_dim = base_dim * 2 ** i_layer
            down_sampler = ConvBN(self.in_channel, embed_dim, 3, 2, 1)
            self.in_channel = embed_dim
            blocks = [Block(self.in_channel, mlp_ratio, dpr[cur + i]) for i in range(depths[i_layer])]
            cur += depths[i_layer]
            self.stages.append(nn.Sequential(down_sampler, *blocks))
        self.channels = [i.size(1) for i in self.forward(torch.randn(1, 3, 640, 640))]
        self.apply(self._init_weights)

    def _init_weights(self, m):
        if isinstance(m, nn.Linear or nn.Conv2d):
            trunc_normal_(m.weight, std=.02)
            if isinstance(m, nn.Linear) and m.bias is not None:
                nn.init.constant_(m.bias, 0)
        elif isinstance(m, nn.LayerNorm or nn.BatchNorm2d):
            nn.init.constant_(m.bias, 0)
            nn.init.constant_(m.weight, 1.0)

    def forward(self, x):
        out=[]
        x = self.stem(x)
        for stage in self.stages:
            x = stage(x)
            out.append(x)
        return out


@register_model
def starnet_s1(pretrained=False, **kwargs):
    model = StarNet(24, [2, 2, 8, 3], **kwargs)
    if pretrained:
        url = model_urls['starnet_s1']
        checkpoint = torch.hub.load_state_dict_from_url(url=url, map_location="cpu")
        model.load_state_dict(checkpoint["state_dict"],strict=False)
    return model


@register_model
def starnet_s2(pretrained=False, **kwargs):
    model = StarNet(32, [1, 2, 6, 2], **kwargs)
    if pretrained:
        url = model_urls['starnet_s2']
        checkpoint = torch.hub.load_state_dict_from_url(url=url, map_location="cpu")
        model.load_state_dict(checkpoint["state_dict"])
    return model


@register_model
def starnet_s3(pretrained=False, **kwargs):
    model = StarNet(32, [2, 2, 8, 4], **kwargs)
    if pretrained:
        url = model_urls['starnet_s3']
        checkpoint = torch.hub.load_state_dict_from_url(url=url, map_location="cpu")
        model.load_state_dict(checkpoint["state_dict"])
    return model


@register_model
def starnet_s4(pretrained=False, **kwargs):
    model = StarNet(32, [3, 3, 12, 5], **kwargs)
    if pretrained:
        url = model_urls['starnet_s4']
        checkpoint = torch.hub.load_state_dict_from_url(url=url, map_location="cpu")
        model.load_state_dict(checkpoint["state_dict"])
    return model


# very small networks #
@register_model
def starnet_s050(pretrained=False, **kwargs):
    return StarNet(16, [1, 1, 3, 1], 3, **kwargs)


@register_model
def starnet_s100(pretrained=False, **kwargs):
    return StarNet(20, [1, 2, 4, 1], 4, **kwargs)


@register_model
def starnet_s150(pretrained=False, **kwargs):
    return StarNet(24, [1, 2, 4, 2], 3, **kwargs)


if __name__ == "__main__":
    init = torch.randn(1, 3, 640, 640).cuda()
    models = starnet_s1(pretrained=True).cuda()
    out = models(init)
    for i in out:
        print(i.shape)

运行代码，出现结果：
在这里插入图片描述
则表明没有问题了！

改进方法

在项目的根目录添加train.py脚本，代码如下：

```bash
from ultralytics import YOLO
import os

if __name__ == '__main__':
    # 加载模型
    model = YOLO(model="ultralytics/cfg/models/v8/yolov8l.yaml")  # 从头开始构建新模型

    # Use the model
    results = model.train(data="VOC.yaml", epochs=300, device='0', batch=8, seed=42,)  # 训练模

训练完成后，就可以看到测试结果！

在项目的根目录添加val.py脚本，代码如下：


from ultralytics import YOLO


if __name__ == '__main__':
    # Load a model
    # model = YOLO('yolov8m.pt')  # load an official model
    model = YOLO('runs/detect/train/weights/best.pt')  # load a custom model


    # Validate the model
    metrics = model.val(split='val')  # no arguments needed, dataset and settings remembered

split='val’代表使用验证集做测试，如果改为split=‘test’，则使用测试集做测试！

在项目的根目录添加test.py脚本，代码如下：

from ultralytics import YOLO


if __name__ == '__main__':
    # Load a model
    # model = YOLO('yolov8m.pt')  # load an official model
    model = YOLO('runs/detect/train/weights/best.pt')  # load a custom model
    results = model.predict(source="ultralytics/assets", device='0',save=True)  # predict on an image
    print(results)

test脚本测试assets文件夹下面的图片，save设置为true，则保存图片的测试结果！
在这里插入图片描述

测试结果

YOLOv8l summary: 568 layers, 35588208 parameters, 0 gradients, 125.3 GFLOPs
                 Class     Images  Instances      Box(P          R      mAP50  mAP50-95): 100%|██████████| 15/15 [00:06<00:00,  2.24it/s]
                   all        230       1412      0.962      0.959      0.984      0.738
                   c17        230        131      0.981      0.992      0.995      0.818
                    c5        230         68      0.971      0.987      0.993      0.829
            helicopter        230         43      0.976          1      0.986      0.574
                  c130        230         85      0.966      0.965      0.993      0.675
                   f16        230         57      0.998      0.965      0.981      0.669
                    b2        230          2      0.938          1      0.995      0.797
                 other        230         86      0.987      0.905      0.962      0.527
                   b52        230         70      0.985      0.962      0.981      0.794
                  kc10        230         62      0.995      0.984      0.989      0.844
               command        230         40      0.984      0.975      0.995      0.815
                   f15        230        123      0.939      0.996       0.98      0.656
                 kc135        230         91      0.989      0.988      0.989       0.68
                   a10        230         27          1      0.449      0.872      0.435
                    b1        230         20      0.992       0.95      0.993      0.743
                   aew        230         25      0.952          1      0.964      0.738
                   f22        230         17       0.88          1      0.995      0.767
                    p3        230        105          1      0.966      0.995      0.794
                    p8        230          1       0.81          1      0.995      0.697
                   f35        230         32          1      0.812      0.961      0.538
                   f18        230        125      0.989      0.992      0.993      0.826
                   v22        230         41      0.994          1      0.995      0.711
                 su-27        230         31      0.975          1      0.995      0.838
                 il-38        230         27      0.981          1      0.995      0.838
                tu-134        230          1      0.845          1      0.995      0.895
                 su-33        230          2      0.946          1      0.995      0.796
                 an-70        230          2      0.903          1      0.995      0.796
                 tu-22        230         98      0.998          1      0.995      0.827