目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4 .参考文献
- 5.代码获取
1.背景
2024年,M Ghasemi受到自然界中常青藤生长行为启发,提出了常青藤优化算法(Ivy Algorithm, IVYA)。


2.算法原理
2.1算法思想
IVYA模拟常青藤种群的协调有序增长以及扩散和演化过程,其通过一个微分方程和数据密集型的实验过程来建模。IVYA利用附近常青藤的知识来确定生长方向,通过选择最近且最健康的邻居来模拟常青藤在自然中的行为。
2.2算法过程
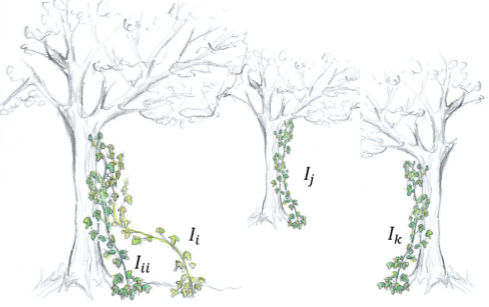
IVYA的研究步骤和种群搜索
常春藤是一种随时间生长的蔓生植物,假设常青藤植物的生长速率Gv是时间的函数,由微分方程给出:
d
G
ν
(
t
)
d
t
=
ψ
⋅
G
ν
(
t
)
⋅
φ
(
G
ν
(
t
)
)
(1)
\frac{dG\nu(t)}{dt}=\psi\cdotp G\nu(t)\cdotp\varphi(G\nu(t))\tag{1}
dtdGν(t)=ψ⋅Gν(t)⋅φ(Gν(t))(1)
其中,Gv为增长率,φ为生长速度,φ为偏离生长的修正系数。成员Ii的生长速度Gvi(t)的差分方程:
Δ
G
v
i
(
t
+
1
)
=
r
a
n
d
2
⊙
(
N
(
1
,
D
)
⊙
Δ
G
v
i
(
t
)
)
(2)
\Delta Gv_i(t+1)=rand^2\odot(N(1,D)\odot\Delta Gv_i(t))\tag{2}
ΔGvi(t+1)=rand2⊙(N(1,D)⊙ΔGvi(t))(2)
其中,向量ΔGvi(t)和ΔGvi(t1)表示离散时间系统(时刻t和时刻t1)的增长率。
成员Ii利用成员Iii沿着光源的方向进行攀爬和移动:
I
i
n
e
w
=
I
i
+
∣
N
(
1
,
D
)
∣
⊙
(
I
i
i
−
I
i
)
+
N
(
1
,
D
)
⊙
Δ
G
v
i
,
i
=
1
,
2
,
.
.
.
,
N
p
o
p
(3)
I_i^{new}=I_i+|N(1,D)|\odot(I_{ii}-I_i)+N(1,D)\odot\Delta Gv_i, i=1,2,...,Npop\tag{3}
Iinew=Ii+∣N(1,D)∣⊙(Iii−Ii)+N(1,D)⊙ΔGvi,i=1,2,...,Npop(3)
在成员Ii通过搜索空间全局漫游到最近的邻居Iii的阶段之后,成员Ii试图直接跟随整个种群的最佳成员IBest,这相当于在成员IBest周围寻找更好的最优解。
I
i
n
e
w
=
I
B
e
s
t
⊙
(
r
a
n
d
(
1
,
D
)
+
N
(
1
,
D
)
⊙
Δ
G
v
i
)
(4)
I_i^{new}=I_{Best}\odot(rand(1,D)+N(1,D)\odot\Delta Gv_i)\tag{4}
Iinew=IBest⊙(rand(1,D)+N(1,D)⊙ΔGvi)(4)
当前成员Inew i的增长率:
Δ
G
ν
i
n
e
w
=
I
i
n
e
w
⊘
(
I
m
a
x
−
I
m
i
n
)
(5)
\Delta G\nu_{i}^{new}=I_{i}^{new}\oslash(I_{max}-I_{min})\tag{5}
ΔGνinew=Iinew⊘(Imax−Imin)(5)
伪代码

3.结果展示
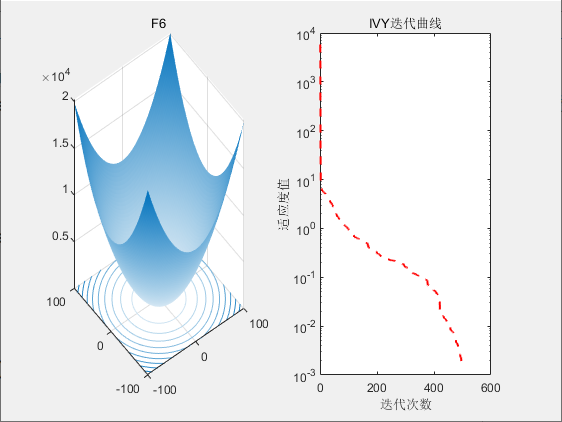
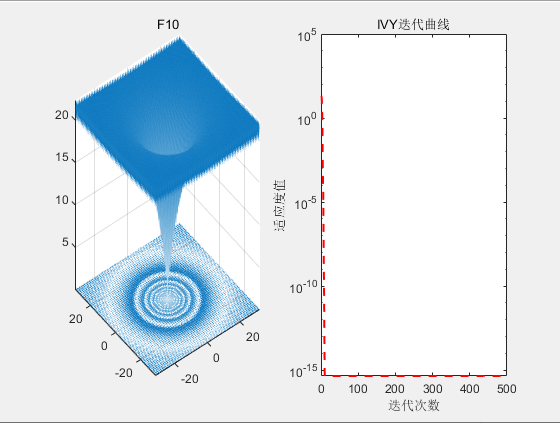
4 .参考文献
[1] Ghasemi M, Zare M, Trojovský P, et al. Optimization based on the smart behavior of plants with its engineering applications: Ivy algorithm[J]. Knowledge-Based Systems, 2024, 295: 111850.






![[linux] 系统的基本使用](https://img-blog.csdnimg.cn/direct/0a70bd16dec04b5493d80de80b351d0e.png)