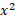menji 和 gcd

题目：

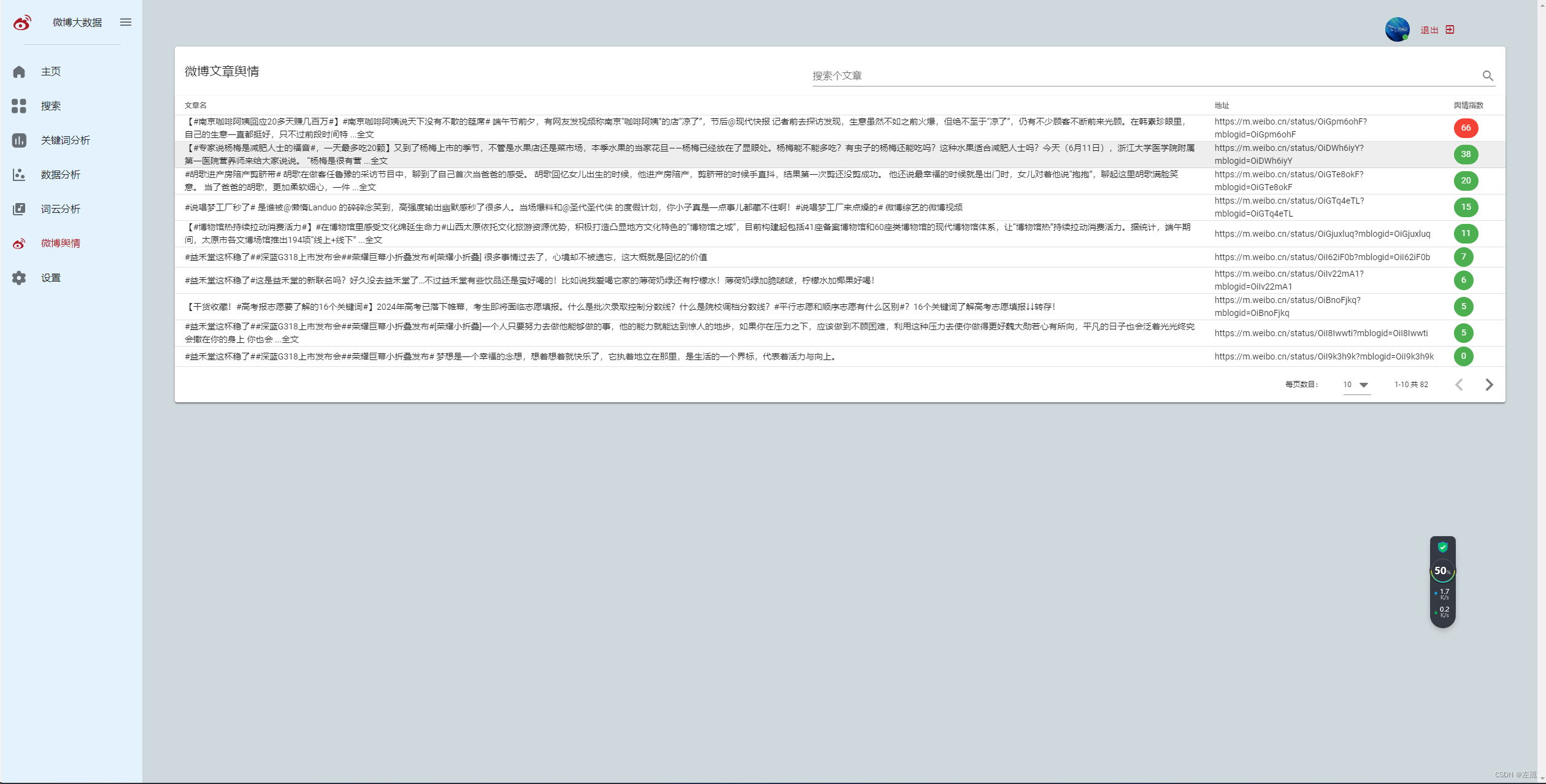
一开始以为是只有l不确定，r是确定的，这样的话我们可以枚举r的所有约数，然后对其每个约数x进行判断，判断是否满足题意，具体做法是先让l % x如果 == 0则该约数可行，如果不可行且余数是y，那么就让l 加上x - y判断这个数是否比r大。时间复杂度o(sqrt(R));

但是现在两端点都是不确定的，注意到 l <= k * g < (k + 1) * g <= r 注意到我们想要得到的gcd与k的乘积是不大于r的，因此这两个未知量的较小值是不大于sqrt(R)的，因此我们可以枚举较小值i，另一个值自然可以通过R / i得到 由于在循环中k * g <= r 是一定的，因此在判断方案是否合法时只需要判断左边界l是否满足即可

代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

void solve() {
    LL l, r;
    cin >> l >> r;
    LL ans = 0;
    for(LL i = 1; i <= r / i; i ++ ) {
        LL j = r / i;
        if((i - 1) * j >= l) ans = max(ans, j);
        if((j - 1) * i >= l) ans = max(ans, i); 
    }
    cout << ans << endl;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while(t -- ) {
        solve();
    }
    return 0;
}

模方程

题目：

显而易见，如果a = b x将会有无穷个，如果 a <  b x将为0

现在思考a > b的情况

a = k * x + b

x = (a - b) / k;

因此k一定是(a - b)的一个因数

枚举所有因数t并判断原式是否成立

代码：

#include <bits/stdc++.h>

using namespace std;

int gcd(int a, int b) {
    return b? gcd(b, a % b): a;
}

int main() {
    int a, b;
    cin >> a >> b;
    vector<int> d;
    if(b == a) cout << "infinity";
    else {
        if(b > a) cout << "0";
        else {
            int tot = a - b;
            for(int i = 1; i <= tot / i; i ++ ) {
                if(tot % i == 0) {
                    d.push_back(i);
                    if(i != tot / i) d.push_back(tot / i);
                }
            }
            int ans = 0;
            for(auto t: d) {
                int x = tot / t;
                if(x < a) ans ++;
            }
            cout << ans;
        }
    }
    return 0;
}