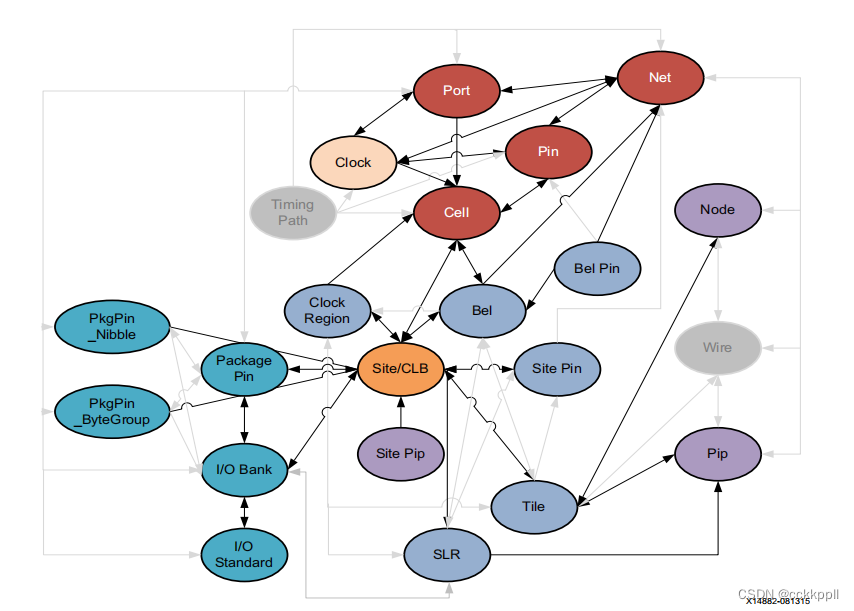
现在再回到洛伦兹变换，

将其写成上角标表示惯性系的形式（注意不是幂次），

并且认为洛伦兹变换中的两个方程的比例常数，

并不仅仅是因为虚数单位数量巨大导致的“误判”，虽然这也是说得通的。因为我们已经看到，长度这个概念，在不同的条件下，对应了不同的基本物理量：在宏观低速条件下它对应的是周期的重复次数，而在微观高速的条件下对应的是频率的差异总量。如果为宏观低速惯性系中的坐标，为微观高速惯性系中的坐标，那么，从微观高速惯性系投射到宏观低速惯性系，就可以使用频差度量，

而反过来，则应当使用周期度量，

而根据周期和频率的倒数关系，

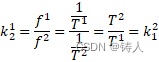
所以

在此可以严格成立，也就是说，确实可以写出，

由此也可以导出，

以及光速上限。但这些都不影响以及代表的频差或者周期比率的意义，所以说，确实可以有光速上限，但并不影响“超光速”的实现。只是在“超光速”的前提下，这种周期和频率互为倒数的对称性不再保持，当然要说明的是，这是对于观察者来说的，这里的观察者既不是也不是，而是第三方观察者：当我们写出和的时候，我们就是第三方观察者，虽然我们也可以是二者之一。