空间复杂度的相关概念

news2024/11/17 9:34:10

1. 空间复杂度

空间复杂度（space complexity）用于衡量算法占用内存空间随着数据量变大时的增长趋势。

统计哪些空间：
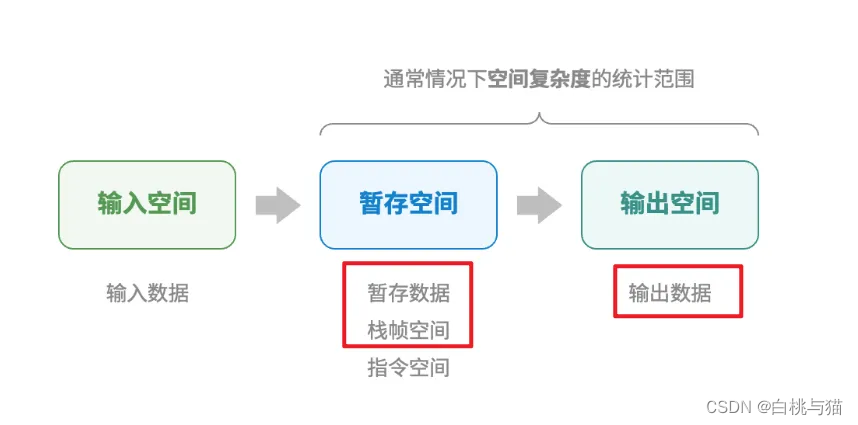
在这里插入图片描述

● 暂存数据：用于保存算法运行过程中的各种常量、变量、对象等。
● 栈帧空间：用于保存调用函数的上下文数据。系统在每次调用函数时都会在栈顶部创建一个栈帧，函数返回后，栈帧空间会被释放。
● 指令空间：用于保存编译后的程序指令，在实际统计中通常忽略不计。

而与时间复杂度不同的是，我们通常只关注最差空间复杂度。这是因为内存空间是一项硬性要求，我们必须确保在所有输入数据下都有足够的内存空间预留。

2. 如何推算

最差空间复杂度中的“最差”有两层含义：
● 以最差输入数据为准：当 n<10 时，空间复杂度为 O(1) ；但当 n>10 时，初始化的数组 nums 占用 O(n) 空间，因此最差空间复杂度为 O(n) 。

function algorithm(n) {
    const a = 0;                   // O(1)
    const b = new Array(10000);    // O(1)
    if (n > 10) {
        const nums = new Array(n); // O(n)
    }
}

● 以算法运行中的峰值内存为准：例如，程序在执行最后一行之前，占用 O(1) 空间；当初始化数组 nums 时，程序占用 O(n) 空间，因此最差空间复杂度为 O(n) 。

function constFunc() {
    // 执行某些操作
    return 0;
}
/* 循环的空间复杂度为 O(1) */
function loop(n) {
    for (let i = 0; i < n; i++) {
        constFunc();
    }
}
/* 递归的空间复杂度为 O(n) */
function recur(n) {
    if (n === 1) return;
    return recur(n - 1);
}

在循环中每轮调用函数，会返回并释放掉栈帧空间，因此只会占用 $O (1)$ 的栈帧空间。
而在递归运行中会同时存在多个未返回的函数，所以会占用 $O (n)$ 的栈帧空间

3. 常见类型

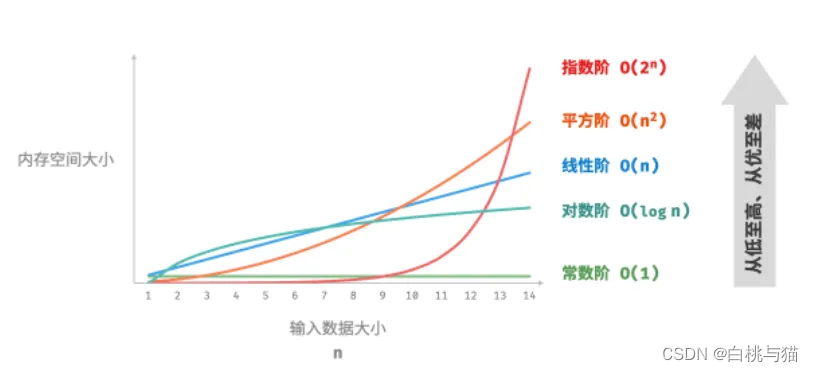
在这里插入图片描述

注意：该图展示的是空间复杂度，其反映的是增长趋势，而不是占用空间的绝对大小。

3.1 常数阶O(1)

常数阶常见于数量与输入数据大小 n 无关的常量、变量、对象。
需要注意的是，在循环中初始化变量或调用函数而占用的内存，在进入下一循环后就会被释放，因此不会累积占用空间，空间复杂度仍为 $O (1)$ ：

/* 函数 */
function constFunc() {
    // 执行某些操作
    return 0;
}

/* 常数阶 */
function constant(n) {
    // 常量、变量、对象占用 O(1) 空间
    const a = 0;
    const b = 0;
    const nums = new Array(10000);
    const node = new ListNode(0);
    // 循环中的变量占用 O(1) 空间
    for (let i = 0; i < n; i++) {
        const c = 0;
    }
    // 循环中的函数占用 O(1) 空间
    for (let i = 0; i < n; i++) {
        constFunc();
    }
}

3.2 线性阶 O(n)

线性阶常见于元素数量与 n 成正比的数组、链表、栈、队列等

/* 线性阶 */
function linear(n) {
    // 长度为 n 的数组占用 O(n) 空间
    const nums = new Array(n);
    // 长度为 n 的列表占用 O(n) 空间
    const nodes = [];
    for (let i = 0; i < n; i++) {
        nodes.push(new ListNode(i));
    }
    // 长度为 n 的哈希表占用 O(n) 空间
    const map = new Map();
    for (let i = 0; i < n; i++) {
        map.set(i, i.toString());
    }
}

每个部分的空间复杂度都是 $O (n)$ ，而这些部分是独立的，不相互嵌套或共享空间。因此，整个函数的空间复杂度为各部分空间复杂度之和（通常忽略常数系数）
最终，该函数的空间复杂度是 $O (n)$ 。

3.3 平方阶

平方阶常见于矩阵和图

/* 平方阶 */
function quadratic(n) {
    // 矩阵占用 O(n^2) 空间
    const numMatrix = Array(n)
        .fill(null)
        .map(() => Array(n).fill(null));
    // 二维列表占用 O(n^2) 空间
    const numList = [];
    for (let i = 0; i < n; i++) {
        const tmp = [];
        for (let j = 0; j < n; j++) {
            tmp.push(0);
        }
        numList.push(tmp);
    }
}

3.4 指数阶

指数阶常见于二叉树，层数为 n 的“满二叉树”的节点数量为 $2^n-1$ ，占用 $O(2^n)$ 空间

/* 指数阶（建立满二叉树） */
function buildTree(n) {// n为深度
    if (n === 0) return null;
    const root = new TreeNode(0);
    root.left = buildTree(n - 1);
    root.right = buildTree(n - 1);
    return root;
}