【NOI-题解】1431. 迷宫的第一条出路

news2024/11/18 18:23:09

文章目录

一、前言
二、问题
- 问题：1431. 迷宫的第一条出路
三、感谢

一、前言

二、问题

问题：1431. 迷宫的第一条出路

类型：深度搜索、回溯、路径打印

题目描述：

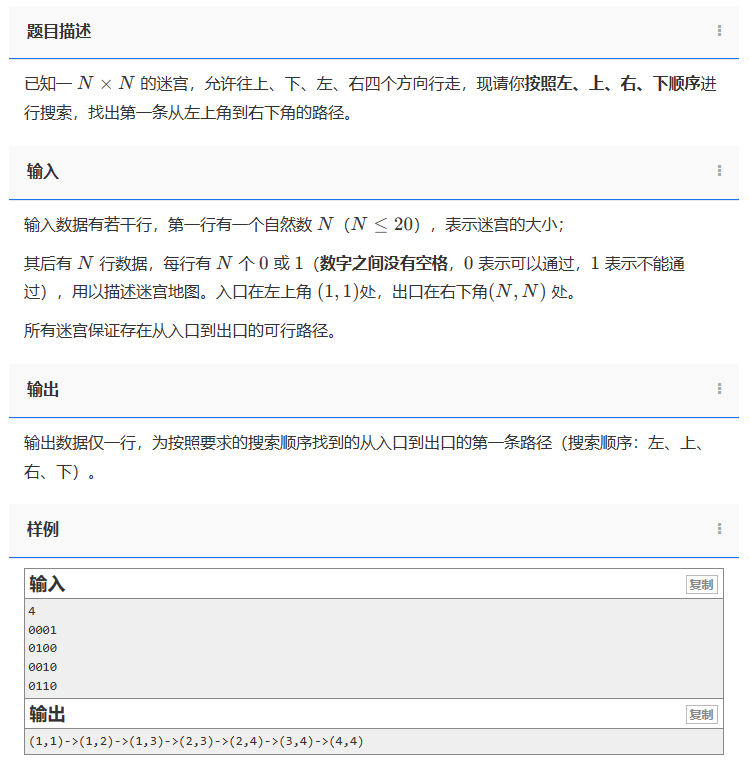
已知一 N×N 的迷宫，允许往上、下、左、右四个方向行走，现请你按照左、上、右、下顺序进行搜索，找出第一条从左上角到右下角的路径。

输入：

输入数据有若干行，第一行有一个自然数 N（N≤20），表示迷宫的大小；
其后有 N 行数据，每行有 N 个 0 或 1（数字之间没有空格，0 表示可以通过，1 表示不能通过），用以描述迷宫地图。入口在左上角 (1,1)处，出口在右下角(N,N) 处。
所有迷宫保证存在从入口到出口的可行路径。

输出：

输出数据仅一行，为按照要求的搜索顺序找到的从入口到出口的第一条路径（搜索顺序：左、上、右、下）。

样例：

输入：

输出：

(1,1)->(1,2)->(1,3)->(2,3)->(2,4)->(3,4)->(4,4)

在这里插入图片描述

1.分析问题

已知：N×N 的迷宫，允许往上、下、左、右四个方向行走。
未知：按照左、上、右、下顺序进行搜索，找出第一条从左上角到右下角的路径。
关系：深度搜索、回溯。

2.定义变量

定义变量：n表示迷宫的大小；二维数组mg[30][30]存储迷宫信息，其中0代表可通行，1代表障碍；二维数组bj[1000][1000]用于记录路径上的坐标。

int n,mg[30][30],bj[1000][1000];

3.输入数据

//三、数据输入
	cin>>n; 
	for(int i=1;i<=n;i++){
		string s;
		cin>>s;
		for(int j=1;j<=n;j++){
			mg[i][j]=s[j-1]-'0';
		}
	}

4.数据计算

调用dfs(1,1,1)开始从左上角(1,1)搜索到右下角。

//四、数据计算 
	dfs(1,1,1);

定义一个深度优先搜索（DFS）函数，用于递归探索迷宫路径。

int  dfs(int x,int y,int k){
	if(x<1||x>n||y<1||y>n||mg[x][y]!=0){
		return k;
	}
	
	bj[k][1]=x;
	bj[k][2]=y;
	mg[x][y]=1;
	
	if(x==n&&y==n){
		//五、输出结果 
		for(int i=1;i<=k;i++){
			cout<<"("<<bj[i][1]<<","<<bj[i][2]<<")";
			if(i!=k){
				cout<<"->";
			}
		}
	}
	//左 
	dfs(x,y-1,k+1); 
	//上
	dfs(x-1,y,k+1);
	//右
	dfs(x,y+1,k+1);
	//下 
	dfs(x+1,y,k+1);
}

完整代码如下：

#include<bits/stdc++.h> // 包含C++常用库函数
using namespace std; // 使用std命名空间以简化代码

int n, // 迷宫的尺寸
    mg[30][30], // 用于存储迷宫地图，0表示可通过，1表示障碍
    bj[1000][1000]; // 记录搜索过程中的路径坐标

// 深度优先搜索函数
// 参数: x, y 当前坐标；k 走过的步数（也作为bj数组的索引）
int dfs(int x, int y, int k){
    // 判断当前位置是否合法或已被访问
    if(x < 1 || x > n || y < 1 || y > n || mg[x][y] != 0){
        return k; // 不合法或已访问过，返回当前步数
    }
    
    // 记录路径
    bj[k][1] = x;
    bj[k][2] = y;
    mg[x][y] = 1; // 标记当前格子已访问
    
    // 如果到达右下角，输出路径并结束
    if(x == n && y == n){
        for(int i = 1; i <= k; i++){
            cout << "(" << bj[i][1] << "," << bj[i][2] << ")";
            if(i != k){ // 非最后一项添加箭头
                cout << "->";
            }
        }
    }
    
    // 递归搜索四个方向
    dfs(x, y-1, k+1); // 左
    dfs(x-1, y, k+1); // 上
    dfs(x, y+1, k+1); // 右
    dfs(x+1, y, k+1); // 下
    
    // 注意：此函数设计上没有直接利用返回值，实际搜索中无需返回具体值
}

int main(){
    // 输入迷宫尺寸
    cin >> n; 
    
    // 输入并构建迷宫地图
    for(int i = 1; i <= n; i++){
        string s;
        cin >> s;
        for(int j = 1; j <= n; j++){
            mg[i][j] = s[j-1] - '0'; // 字符转数字，'0' ASCII值为48，因此减去'0'得到数字
        }
    }
    
    // 开始搜索
    dfs(1, 1, 1); // 从(1,1)开始搜索，初始步数为1
    
    return 0; // 程序正常结束
}