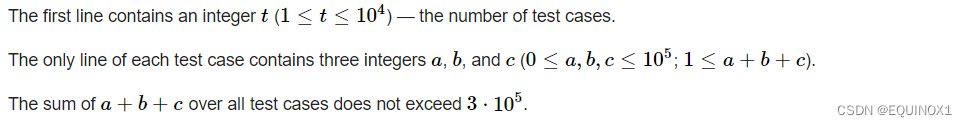一、题目

1、题目描述

2、输入输出

2.1输入

2.2输出

3、原题链接

1950F - 0, 1, 2, Tree!

---

二、解题报告

1、思路分析

考虑让构造n个结点的二叉树如何构造高度最小？

构造完全二叉树，即一层一层放

对于本题，显然我们要先放“2”结点，因为先放0、1显然会有空隙产生，高度变高

放完“2”后，学过二叉树都知道，叶子结点的个数为孩子为2结点个数+1，所以会产生a+1个孩子空位

我们发现由于“1”结点放完后仍然要为其配一个孩子，所以我们放“1”结点不会影响空位

于是思路就有了：

由于a个“2”结点会产生a + 1个空位，而插入“1”不会影响，所以a + 1 = c，用来判断非法

假设a的二进制长度为da，即树高

那么最后一层如果不满会有(1 << da) - a - 1个个空位记为k，我们放“1”结点

如果有剩余的“1”结点，其增加的高度db = （b - k + a） / (a + 1)

然后放c又会增加一层

所以答案就是da + db（注意题目要求高度从0开始）

2、复杂度

时间复杂度： O(T), 即每次O(1)判断 空间复杂度：O(1)

3、代码详解

 ​

import sys
import math
input = lambda: sys.stdin.readline().strip()
MII = lambda: map(int, input().split())
LMI = lambda: list(map(int, input().split()))
I = lambda: int(input())
fmax = lambda x, y: x if x > y else y

P = 998244353

def solve() -> None:
    a, b, c = MII()
    if a + 1 != c:
        print(-1)
        return

    da = a.bit_length()
    resa = (1 << da) - a - 1
    b -= resa
    db = 0 if b < 0 else (b + a) // (a + 1)
    print(da + db)

T = I()
for _ in range(T):
    solve()