1.提升方法是将弱学习算法提升为强学习算法的统计学习方法。在分类学习中,提升方法通过反复修改训练数据的权值分布,构建一系列基本分类器(弱分类器),并将这些基本分类器线性组合,构成一个强分类器。代表性的提升方法是AdaBoost算法。
AdaBoost模型是弱分类器的线性组合:
f ( x ) = ∑ m = 1 M α m G m ( x ) f(x)=\sum_{m=1}^{M} \alpha_{m} G_{m}(x) f(x)=m=1∑MαmGm(x)
2.AdaBoost算法的特点是通过迭代每次学习一个基本分类器。每次迭代中,提高那些被前一轮分类器错误分类数据的权值,而降低那些被正确分类的数据的权值。最后,AdaBoost将基本分类器的线性组合作为强分类器,其中给分类误差率小的基本分类器以大的权值,给分类误差率大的基本分类器以小的权值。
3.AdaBoost的训练误差分析表明,AdaBoost的每次迭代可以减少它在训练数据集上的分类误差率,这说明了它作为提升方法的有效性。
4.AdaBoost算法的一个解释是该算法实际是前向分步算法的一个实现。在这个方法里,模型是加法模型,损失函数是指数损失,算法是前向分步算法。
每一步中极小化损失函数
( β m , γ m ) = arg min β , γ ∑ i = 1 N L ( y i , f m − 1 ( x i ) + β b ( x i ; γ ) ) \left(\beta_{m}, \gamma_{m}\right)=\arg \min _{\beta, \gamma} \sum_{i=1}^{N} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+\beta b\left(x_{i} ; \gamma\right)\right) (βm,γm)=argβ,γmini=1∑NL(yi,fm−1(xi)+βb(xi;γ))
得到参数 β m , γ m \beta_{m}, \gamma_{m} βm,γm。
5.提升树是以分类树或回归树为基本分类器的提升方法。提升树被认为是统计学习中最有效的方法之一。
1 袋装(bagging)提升(boosting)的区别
袋装 ( B a g g i n g ) (Bagging) (Bagging)和提升 ( B o o s t i n g ) (Boosting) (Boosting)是两种常见的集成学习方法,它们通过结合多个基模型来提高模型的性能。尽管它们的目标相似,但在具体实现和策略上有显著的区别。
- 袋装 ( b a g g i n g ) (bagging) (bagging)是 Bootstrap Aggregating 的简称,它通过在训练集中进行有放回的随机抽样生成多个不同的子集,然后在这些子集上训练多个基模型(通常是同一类型的模型,如决策树),最后将这些基模型的预测结果进行平均(回归问题)或投票(分类问题)。
- 提升 ( b o o s t i n g ) (boosting) (boosting)通过逐步训练基模型,每个基模型都试图修正前一个基模型的错误。每一轮训练中,错误分类的样本会被赋予更高的权重,以便下一轮训练能够更好地处理这些难以分类的样本。
2 AdaBoost
AdaBoost是AdaptiveBoost的缩写,表明该算法是具有适应性的提升算法。
算法的步骤如下:
1)给每个训练样本( x 1 , x 2 , … . , x N x_{1},x_{2},….,x_{N} x1,x2,….,xN)分配权重,初始权重 w 1 w_{1} w1均为 1 / N 1/N 1/N。
2)针对带有权值的样本进行训练,得到模型 G m G_m Gm(初始模型为 G 1 G1 G1)。
3)计算模型 G m G_m Gm的误分率 e m = ∑ i = 1 N w i I ( y i ≠ G m ( x i ) ) e_m=\sum_{i=1}^Nw_iI(y_i\not= G_m(x_i)) em=∑i=1NwiI(yi=Gm(xi))
4)计算模型 G m G_m Gm的系数 α m = 0.5 log [ ( 1 − e m ) / e m ] \alpha_m=0.5\log[(1-e_m)/e_m] αm=0.5log[(1−em)/em]
5)根据误分率 e e e和当前权重向量 w m w_m wm更新权重向量 w m + 1 w_{m+1} wm+1。
6)计算组合模型 f ( x ) = ∑ m = 1 M α m G m ( x i ) f(x)=\sum_{m=1}^M\alpha_mG_m(x_i) f(x)=∑m=1MαmGm(xi)的误分率。
7)当组合模型的误分率或迭代次数低于一定阈值,停止迭代;否则,回到步骤 2)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from matplotlib_inline import backend_inline
backend_inline.set_matplotlib_formats('svg')
# data
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data)
df['label'] = iris.target
df.columns = [
'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
]
data = np.array(df.iloc[:100, [0, 1, -1]])
for i in range(len(data)):
if data[i, -1] == 0:
data[i, -1] = -1
# print(data)
return data[:, :2], data[:, -1]
X,y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 2)
plt.scatter(X[:50, 0], X[:50, 1], label='0')
plt.scatter(X[50:, 0], X[50:, 1], label='1')
plt.legend()
plt.show()

2.1 Adaboost代码实现(二分类)
class AdaBoost:
def __init__(self, n_estimators=50, learning_rate=1.0):
self.clf_num = n_estimators
self.learning_rate = learning_rate
def init_args(self, datasets, labels):
self.X = datasets
self.Y = labels
self.M, self.N = datasets.shape
# 弱分类器数目和集合
self.clf_sets = []
# 初始化weights
self.weights = [1.0 / self.M] * self.M
# G(x)系数 alpha
self.alpha = []
# 实现单一弱分类器
def _G(self, features, labels, weights):
m = len(features) # 样本数量
error = 100000.0 # 无穷大
best_v = 0.0
# 单维features
features_min = min(features) # 这列特征最小的值
features_max = max(features) # 这列特征最大的值
n_step = (features_max - features_min +
self.learning_rate) // self.learning_rate
# print('n_step:{}'.format(n_step))
current_direct, compare_array,best_direct = None, None,None
# 遍历所有可能的阈值 v,以找到最佳的分类阈值。
# 对每个阈值,计算正向和负向分类器的加权分类误差。
# 选择误差较小的分类器,并更新最优分类器的阈值和分类结果
for i in range(1, int(n_step)):
v = features_min + self.learning_rate * i
# 避免在已有特征值上进行分割
if v not in features:
# 误分类计算:特征值大于阈值 v,则分类为 1,否则分类为 -1
compare_array_positive = np.array(
[1 if features[k] > v else -1 for k in range(m)])
# 使用正向分类器时的加权分类误差,计算分类结果与标签不一致的样本权重之和
weight_error_positive = sum([
weights[k] for k in range(m)
if compare_array_positive[k] != labels[k]
])
compare_array_nagetive = np.array(
[-1 if features[k] > v else 1 for k in range(m)])
weight_error_nagetive = sum([
weights[k] for k in range(m)
if compare_array_nagetive[k] != labels[k]
])
# 比较正向和负向分类器的误差,选择误差较小的分类器,并记录相应的分类结果数组 _compare_array 和分类方向
if weight_error_positive < weight_error_nagetive:
weight_error = weight_error_positive
_compare_array = compare_array_positive
current_direct = 'positive'
else:
weight_error = weight_error_nagetive
_compare_array = compare_array_nagetive
current_direct = 'nagetive'
# print('v:{} error:{}'.format(v, weight_error))
if weight_error < error:
error = weight_error
compare_array = _compare_array
best_v = v
best_direct = current_direct
return best_v, best_direct, error, compare_array
# 计算alpha
def _alpha(self, error):
return 0.5 * np.log((1 - error) / error)
# 规范化因子
def _Z(self, weights, a, clf):
return sum([
weights[i] * np.exp(-1 * a * self.Y[i] * clf[i])
for i in range(self.M)
])
# 权值更新
def _w(self, a, clf, Z):
for i in range(self.M):
self.weights[i] = self.weights[i] * np.exp(
-1 * a * self.Y[i] * clf[i]) / Z
# G(x)的线性组合
def _f(self, alpha, clf_sets):
pass
def G(self, x, v, direct):
if direct == 'positive':
return 1 if x > v else -1
else:
return -1 if x > v else 1
def fit(self, X, y):
self.init_args(X, y)
# 每轮迭代中,找到误差最小的弱分类器,计算其权重,并更新样本权重
for epoch in range(self.clf_num):
best_clf_error, best_v, clf_result, final_direct = 100000, None, None, None
# 根据特征维度, 选择误差最小的维度
for j in range(self.N):
features = self.X[:, j]
# 分类阈值,分类方向,分类误差,分类结果
v, direct, error, compare_array = self._G(
features, self.Y, self.weights)
if error < best_clf_error:
best_clf_error = error
best_v = v
final_direct = direct
clf_result = compare_array
axis = j
# print('epoch:{}/{} feature:{} error:{} v:{}'.format(epoch, self.clf_num, j, error, best_v))
if best_clf_error == 0:
break
# 计算G(x)系数a
a = self._alpha(best_clf_error)
self.alpha.append(a)
# 记录分类器
self.clf_sets.append((axis, best_v, a,final_direct))
# 规范化因子
Z = self._Z(self.weights, a, clf_result)
# 权值更新
self._w(a, clf_result, Z)
# print('classifier:{}/{} error:{:.3f} v:{} direct:{} a:{:.5f}'.format(epoch+1, self.clf_num, error, best_v, final_direct, a))
# print('weight:{}'.format(self.weights))
# print('\n')
def predict(self, feature):
result = 0.0
for i in range(len(self.clf_sets)):
axis, clf_v, _a, direct = self.clf_sets[i]
f_input = feature[axis]
result += self.alpha[i] * self.G(f_input, clf_v, direct)
# sign
return 1 if result > 0 else -1
def score(self, X_test, y_test):
right_count = 0
for i in range(len(X_test)):
feature = X_test[i]
if self.predict(feature) == y_test[i]:
right_count += 1
return right_count / len(X_test)
2.2 例题8.1
X = np.arange(10).reshape(10, 1)
y = np.array([1, 1, 1, -1, -1, -1, 1, 1, 1, -1])
clf = AdaBoost(n_estimators=3, learning_rate=0.5)
clf.fit(X, y)
clf.clf_sets
[(0, 2.5, 0.4236489301936017, 'nagetive'),
(0, 8.5, 0.6496414920651304, 'nagetive'),
(0, 5.5, 0.752038698388137, 'positive')]
clf = AdaBoost(n_estimators=10, learning_rate=0.2)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
0.8666666666666667
# 50次结果
result = []
for i in range(1, 51):
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
clf = AdaBoost(n_estimators=100, learning_rate=0.2)
clf.fit(X_train, y_train)
r = clf.score(X_test, y_test)
# print('{}/100 score:{}'.format(i, r))
result.append(r)
print('average score:{:.3f}'.format(np.mean(result)))
average score:0.839
2.3 sklearn.ensemble.AdaBoostClassifier
-
a l g o r i t h m algorithm algorithm:这个参数只有AdaBoostClassifier有。主要原因是scikit-learn实现了两种Adaboost分类算法,SAMME和SAMME.R。两者的主要区别是弱学习器权重的度量,SAMME使用了和原理篇里二元分类Adaboost算法的扩展,即用对样本集分类效果作为弱学习器权重,而SAMME.R使用了对样本集分类的预测概率大小来作为弱学习器权重。由于SAMME.R使用了概率度量的连续值,迭代一般比SAMME快,因此AdaBoostClassifier的默认算法algorithm的值也是SAMME.R。我们一般使用默认的SAMME.R就够了,但是要注意的是使用了SAMME.R, 则弱分类学习器参数base_estimator必须限制使用支持概率预测的分类器。SAMME算法则没有这个限制。
-
n _ e s t i m a t o r s n\_estimators n_estimators:AdaBoostClassifier和AdaBoostRegressor都有,就是弱学习器的最大迭代次数,或者说最大的弱学习器的个数。一般来说n_estimators太小,容易欠拟合,n_estimators太大,又容易过拟合,一般选择一个适中的数值。默认是50。在实际调参的过程中,常常将n_estimators和下面介绍的参数learning_rate一起考虑。
-
l e a r n i n g _ r a t e learning\_rate learning_rate:AdaBoostClassifier和AdaBoostRegressor都有,即每个弱学习器的权重缩减系数 ν ν ν。
-
b a s e _ e s t i m a t o r base\_estimator base_estimator:AdaBoostClassifier和AdaBoostRegressor都有,即弱分类学习器或者弱回归学习器。理论上可以选择任何一个分类或者回归学习器,不过需要支持样本权重。常用的一般是CART决策树或者神经网络MLP。
-
r a n d o m _ s t a t e random\_state random_state:整数、随机数生成器实例或 None,默认为 None。用于控制随机数生成,以便结果可重现。
from sklearn.ensemble import AdaBoostClassifier
clf = AdaBoostClassifier(n_estimators=100, learning_rate=0.5)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
0.9
2.3.1 sklearn完整示例
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 初始化 AdaBoost 分类器
# 使用默认的决策树分类器作为弱学习器
clf = AdaBoostClassifier(n_estimators=50, learning_rate=1.0, random_state=42)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")
# 查看模型的弱学习器
print(f"Number of weak learners: {len(clf.estimators_)}")
Accuracy: 1.00
Number of weak learners: 50
- b a s e _ e s t i m a t o r base\_estimator base_estimator:可以自定义弱学习器,例如,使用深度为 2 的决策树:
base_clf = DecisionTreeClassifier(max_depth=2)
clf = AdaBoostClassifier(base_estimator=base_clf, n_estimators=50, learning_rate=1.0, random_state=42)
3 第八章的课后习题
8.1 某公司招聘职员考查身体、业务能力、发展潜力这3项。身体分为合格1、不合格0两级,业务能力和发展潜力分为上1、中2、下3三级分类为合格1 、不合格-1两类。已知10个人的数据,如下表所示。假设弱分类器为决策树桩。试用AdaBoost算法学习一个强分类器。
应聘人员情况数据表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 身体 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 业务 | 1 | 3 | 2 | 1 | 2 | 1 | 1 | 1 | 3 | 2 |
| 潜力 | 3 | 1 | 2 | 3 | 3 | 2 | 2 | 1 | 1 | 1 |
| 分类 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | -1 | -1 |
import numpy as np
# 加载训练数据
X = np.array([[0, 1, 3], [0, 3, 1], [1, 2, 2], [1, 1, 3], [1, 2, 3], [0, 1, 2],
[1, 1, 2], [1, 1, 1], [1, 3, 1], [0, 2, 1]])
y = np.array([-1, -1, -1, -1, -1, -1, 1, 1, -1, -1])
AdaBoostClassifier分类器实现:
采用sklearn的AdaBoostClassifier分类器直接求解,由于AdaBoostClassifier分类器默认采用CART决策树弱分类器,故不需要设置base_estimator参数。
from sklearn.ensemble import AdaBoostClassifier
clf = AdaBoostClassifier()
clf.fit(X, y)
y_predict = clf.predict(X)
score = clf.score(X, y)
print("原始输出:", y)
print("预测输出:", y_predict)
print("预测正确率:{:.2%}".format(score))
原始输出: [-1 -1 -1 -1 -1 -1 1 1 -1 -1]
预测输出: [-1 -1 -1 -1 -1 -1 1 1 -1 -1]
预测正确率:100.00%
自编程实现
# 自编程求解习题8.1
import numpy as np
class AdaBoost:
def __init__(self, X, y, tol=0.05, max_iter=10):
# 训练数据 实例
self.X = X
# 训练数据 标签
self.y = y
# 训练中止条件 right_rate>self.tol
self.tol = tol
# 最大迭代次数
self.max_iter = max_iter
# 初始化样本权重w
self.w = np.full((X.shape[0]), 1 / X.shape[0])
self.G = [] # 弱分类器
def build_stump(self):
"""
以带权重的分类误差最小为目标,选择最佳分类阈值
best_stump['dim'] 合适的特征所在维度
best_stump['thresh'] 合适特征的阈值
best_stump['ineq'] 树桩分类的标识lt,rt
"""
m, n = np.shape(self.X)
# 分类误差
e_min = np.inf
# 小于分类阈值的样本属于的标签类别
sign = None
# 最优分类树桩
best_stump = {}
for i in range(n):
range_min = self.X[:, i].min() # 求每一种特征的最大最小值
range_max = self.X[:, i].max()
step_size = (range_max - range_min) / n
for j in range(-1, int(n) + 1):
thresh_val = range_min + j * step_size
# 计算左子树和右子树的误差
for inequal in ['lt', 'rt']:
predict_vals = self.base_estimator(self.X, i, thresh_val,
inequal)
err_arr = np.array(np.ones(m))
err_arr[predict_vals.T == self.y.T] = 0
weighted_error = np.dot(self.w, err_arr)
if weighted_error < e_min:
e_min = weighted_error
sign = predict_vals
best_stump['dim'] = i
best_stump['thresh'] = thresh_val
best_stump['ineq'] = inequal
return best_stump, sign, e_min
def updata_w(self, alpha, predict):
"""
更新样本权重w
"""
# 以下2行根据公式8.4 8.5 更新样本权重
P = self.w * np.exp(-alpha * self.y * predict)
self.w = P / P.sum()
@staticmethod
def base_estimator(X, dimen, threshVal, threshIneq):
"""
计算单个弱分类器(决策树桩)预测输出
"""
ret_array = np.ones(np.shape(X)[0]) # 预测矩阵
# 左叶子 ,整个矩阵的样本进行比较赋值
if threshIneq == 'lt':
ret_array[X[:, dimen] <= threshVal] = -1.0
else:
ret_array[X[:, dimen] > threshVal] = -1.0
return ret_array
def fit(self):
"""
对训练数据进行学习
"""
G = 0
for i in range(self.max_iter):
best_stump, sign, error = self.build_stump() # 获取当前迭代最佳分类阈值
alpha = 1 / 2 * np.log((1 - error) / error) # 计算本轮弱分类器的系数
# 弱分类器权重
best_stump['alpha'] = alpha
# 保存弱分类器
self.G.append(best_stump)
# 以下3行计算当前总分类器(之前所有弱分类器加权和)分类效率
G += alpha * sign
y_predict = np.sign(G)
error_rate = np.sum(
np.abs(y_predict - self.y)) / 2 / self.y.shape[0]
if error_rate < self.tol: # 满足中止条件 则跳出循环
print("迭代次数:", i + 1)
break
else:
self.updata_w(alpha, y_predict) # 若不满足,更新权重,继续迭代
def predict(self, X):
"""
对新数据进行预测
"""
m = np.shape(X)[0]
G = np.zeros(m)
for i in range(len(self.G)):
stump = self.G[i]
# 遍历每一个弱分类器,进行加权
_G = self.base_estimator(X, stump['dim'], stump['thresh'],
stump['ineq'])
alpha = stump['alpha']
G += alpha * _G
y_predict = np.sign(G)
return y_predict.astype(int)
def score(self, X, y):
"""对训练效果进行评价"""
y_predict = self.predict(X)
error_rate = np.sum(np.abs(y_predict - y)) / 2 / y.shape[0]
return 1 - error_rate
clf = AdaBoost(X, y)
clf.fit()
y_predict = clf.predict(X)
score = clf.score(X, y)
print("原始输出:", y)
print("预测输出:", y_predict)
print("预测正确率:{:.2%}".format(score))
迭代次数: 8
原始输出: [-1 -1 -1 -1 -1 -1 1 1 -1 -1]
预测输出: [-1 -1 -1 -1 -1 -1 1 1 -1 -1]
预测正确率:100.00%
习题8.2 比较支持向量机、 AdaBoost 、Logistic回归模型的学习策略与算法
解答:
- 支持向量机
学习策略:极小化正则化合页损失,软间隔最大化;
学习算法:序列最小最优化算法(SMO) - AdaBoost
学习策略:极小化加法模型指数损失;
学习算法:前向分步加法算法 - Logistic回归
学习策略:极大似然估计,正则化的极大似然估计;
学习算法:改进的迭代尺度算法,梯度下降,拟牛顿法
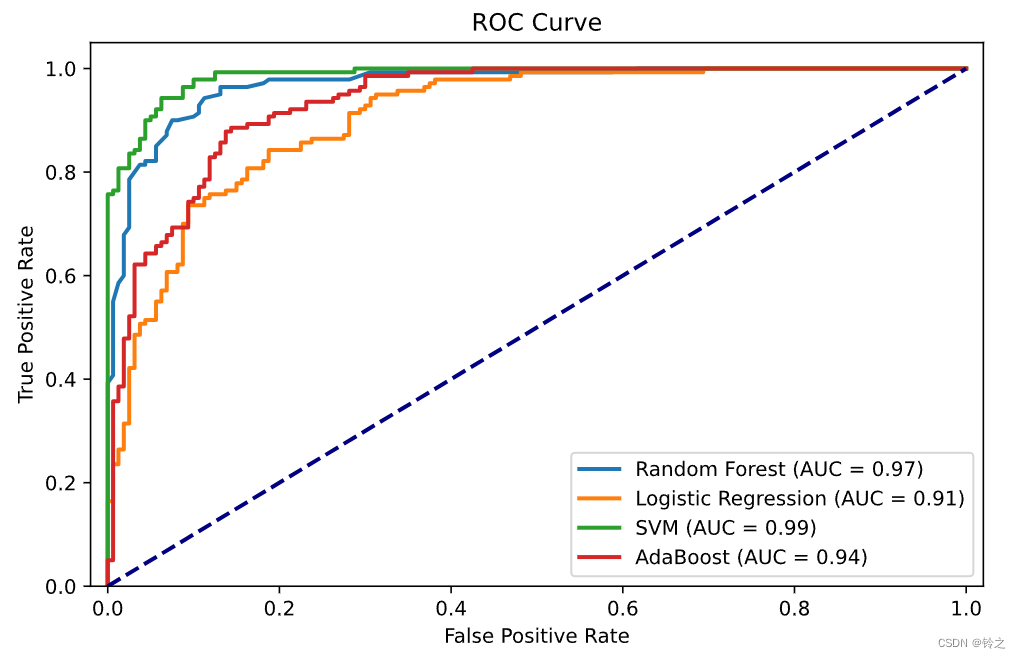
4 一个例子:随机森林、Logistic回归、SVM、AdaBoost
-
使用 m a k e _ c l a s s i f i c a t i o n make\_classification make_classification 数据集生成一个带有 1000 个样本和 20 个特征的二分类数据集,其中有 15 个信息特征和 5 个冗余特征
-
使用随机森林、逻辑回归、SVM 和 AdaBoost 进行分类
-
绘制四个模型的 ROC 曲线,并计算和标出对应的 AUC 值
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.metrics import roc_curve, auc
# 生成数据集
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=42)
# 添加噪声
np.random.seed(42)
noise = np.random.normal(0, 0.1, X.shape)
X += noise
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 定义分类器
classifiers = {
"Random Forest": RandomForestClassifier(n_estimators=100, random_state=42),
"Logistic Regression": LogisticRegression(max_iter=1000, random_state=42),
"SVM": SVC(probability=True, random_state=42),
"AdaBoost": AdaBoostClassifier(n_estimators=100, random_state=42)
}
# 训练分类器并计算 ROC 曲线和 AUC 值
plt.figure(figsize=(8, 5))
for name, clf in classifiers.items():
clf.fit(X_train, y_train)
y_score = clf.predict_proba(X_test)[:, 1]
fpr, tpr, _ = roc_curve(y_test, y_score)
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, lw=2, label=f'{name} (AUC = {roc_auc:.2f})')
# 绘制 ROC 曲线
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([-0.02, 1.02])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend(loc="lower right")
plt.show()
代码来自:https://github.com/fengdu78/lihang-code
参考书籍:李航《机器学习方法》