排序
文章目录
- 排序
- 直接(插入)排序InsertSort
- 思想
- 实现方法:
- 希尔排序ShellSort(可过OJ)
- 思想
- 预排序
- gap的作用
- 整体代码
- 选择排序SelectSort
- 思想
- 完整代码
- 堆排序HeapSort(可过OJ)
- 思想
- 大根堆
- 向下调整
- 完整代码
- 冒泡排序BubbleSort
- 快速排序(快排)QuickSort
- 缺陷
- 三数取中法,规避缺陷情况
- 快排的实现方式
- 双(左右)指针法
- 挖坑法
- 前后指针法
- 快排的非递归方式
- 归并排序(外排序)MergeSort (像后序遍历)(可过OJ)
- 归并排序的内存中(内排序)实现方法
- 归并排序内排序的非递归
- 归并排序的外排序实现方法(加餐)
- 一些小众的排序
- 计数排序
- 基数排序
- 排序算法复杂度及稳定性分析
- 关于稳定性的理解
- 递归的缺陷
- 递归改非递归的方式
- 递归改非递归为什么
- 测试排序的接口
- 测试排序算法的OJ题
- 一些练习题
直接(插入)排序InsertSort
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
思想
把需要排序的数组按大小依次插入到已经排好序的数组里面去,得到一个新的有序数组。
实现方法:
默认数组只有一个数,因为是一个数,所以一定是有序的,然后把将要排序的数组的第二个数拿过来,再逆序遍历已经排好序的数组,也就是那一个数,跟这个数比较大小,一定是大于小于等于这三个里面的一个,如果是递增排序的话,后面是越来越大,那么这个待排序的数如果比已经拍好的数组的最后一个数大的话,直接插入就可以了。如果待排数比已经排好序数组的最后一个数小,就把排好序的数比较的这个数,用它前面的数覆盖,就相当于数据后移了,再把这个待排的数跟前面的数比较大小,如果还小就再覆盖。
void InsertSort(int* a, int n)
{
int end;
int tmp;
int i = 1;
while (i < n)
{
end = i;
tmp = a[end];
// 去找有序数组中哪一个数比tmp小,当然是倒着找了
while (end > 0 && a[end - 1] > tmp)
{
a[end] = a[end - 1];
end--;
}
// 此时end指向的数字是比tmp小的,也可能能找不到比tmp小的,tmp就排到对头上去了
a[end] = tmp;
i++;// i是a数组的第i个数,如果再插入一个数,放在队尾就好了,再运行一遍函数就可以了
}
}
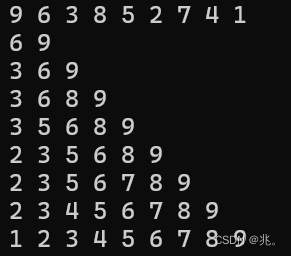
不难发现,随着 i 的增大,每次处理数据的数量也在逐增。因为只有一个数据的时候不用比较,所以直接让i从1开始,也就是至少两个数据才开始比较。
每一次都是把将要插入的数据倒着根其他数据比较,找到合适的位置后插入。保持数组一直有序,也不难发现这种方法最坏的情况是逆序,或者接逆序。上面这个样例中当i走到最后的时候,这个1要移动8次。特别浪费时间。
希尔排序ShellSort(可过OJ)
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
- 希尔排序的时间复杂度不好计算,需要进行推导,推导出来平均时间复杂度: O(N1.3 —N2)
- 稳定性:不稳定
思想
就是对直接插入排序的优化,对于直接插入排序来说,这个序列趋近于有序,时间复杂度就越低。反之,这个当序列杂乱的时候,或者是与题目要求的顺序相反,就会非常浪费时间。所以,希尔对直接排序的代码进行了优化,增加了一个预排序的过程。
预排序
设置gap(间距),把一个完整的数组按照gap分组,对于每一个组再单独进行直接排序。通过预处理过程,可以尽量的使数列趋近于有序。当数列趋近于有序的时候,再使用直接排序对整个序列排序,时间会大大降低。当数据足够大的时候才能更好的展现预排序对直接排序的好处。
gap的作用
gap是对数组预排序的隔断的存在,当gap最大的时候,也就是数组本身的大小,是无意义的。但是比n小一点点,就会有很大的作用。
比如,a[]={9,5,3,4,6,8,7,2,1};
对于直接排序来说,9需要移动9次才能从第一位移动到最后一位。
对于希尔排序来说,当gap为3的时候,9会依次与4,7,进行比较,很明显正确顺序是4,7,9。经过一次排序后,数组就是{4,5,3,7,6,8,9,2,1}.
数组稍微有序一点点,然后是第二位为首元素的时候,间距为gap的数就是{5,6,2},排序后是{2,5,6}.放到原数组就是{4,2,3,7,5,8,9,6,1}.
然后是{3,8,1}》》》{1,3,8}。数组就是{4,2,1,7,5,3,9,6,8}.
不难发现,9已经到了队尾了。8也差不多。这些较大的数已经足够靠后了,像是1,2这些数也足够靠前了。
再缩小gap的值,因为已经有序了,所以时间会越来越快。当gap为1的时候就是直接排序了。又因为足够有序,所以时间复杂度趋近于O(N).
算上前面预排序的时间,最快是O(N1.3),最慢也不到O(N2)
整体代码
void ShellSort(int* a, int n)
{
int end;
int tmp;
int gap = n + 1; // gap要以实际的n为准,实际的n还要大个1
while (gap > 1) // 保证最后一次gap是1,相当于直接排序
{
gap = (gap / 3) + 1;
int i = 0;
while (i <= n)
{
end = i;
tmp = a[end];
while (end > 0 && end-gap >= 0 && a[end - gap] > tmp)
{
a[end] = a[end - gap]; // 和直接排序结构一样,不同的就是直接排序一直是一个一个的比,希尔排序是隔gap位数比一次
end -= gap;
}
a[end] = tmp;
i++;
}
}
}
void Test()
{
int a[] = { 3,-1 };
ShellSort(a, sizeof(a) / sizeof(int) - 1);
Printarray(a, sizeof(a) / sizeof(int));
}
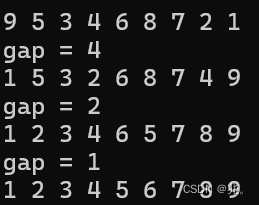
首先是以gap为8/2=4开始排序,和直接排序一样,每次排序的数,都跟前面的数比较,但是希尔排序有了gap这个概念,也就是每次比较的数只能跟这个数前面相隔gap的数比较。这样最后一位的1只需要移动((n/gap)+1)次,就可以到达正确的位置。当前在gap等于1之前,这个数列不一定有序,但是接近有序。
选择排序SelectSort
思想
就是遍历一次数组,找数组的最大值和最小值的下标,然后放在数组的头部和尾部。再缩小数组的大小,头begin后移,尾end前移,当他俩相遇的时候就停止。
所以要一直遍历整个数组,无论这个数组是否是有序的,都要完整的遍历一次数组(从begin到end)。
完整代码
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int min, max;
min = begin;
max = begin;
for (int i = begin + 1; i <= end; i++)
{
if (a[i] < a[min])
min = i;
if (a[i] > a[max])
max = i;
}
Swap(&a[begin], &a[min]);
if (max == begin) // 修正max的位置
max = min;
Swap(&a[end], &a[max]);
begin++;
end--;
}
}

对于第一次循环,最小值是1,最大值是9,所有{1,9}归位,再是{2,8}归位。依次向中间靠拢…
堆排序HeapSort(可过OJ)
堆排序的特性总结:
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
思想
先是建堆。根据需求分为大根堆和小根堆两种情况。
如果是升序,从小到大的顺序,也就是说最小的值在前面。
理清思路后,再好好想想,堆排序只有一次建堆的机会,倘若是建小堆。数组的第一位是最小的数不假。第二次该怎么办呢,是左子节点还是右子节点。如果是右子节点,要不要交换左右子节点的值,后面的节点怎么办?
全是问题。但是逆向思维就好了。比如,大根堆。每次找最大的值,然后把最大的值放在堆底。也就是交换a[0]和a[end]。只需要每次让end前移一次,堆变小了,最二大的数又放到根部了,再交换值。然后向下调整根部。循环即可。
建堆的时间复杂度是O(N),每次向下调整的时间是O(log2N).
差不多就是O(N*logN)了。
大根堆
就是在这个完全二叉树中,根的值,是这颗树最大的值,为了建出这个大根堆,还要保证每个父节点都要大于子节点的值。所以从最后一个父节点开始,逆向向下调整。
向下调整
以当前节点为父节点,判断它的子节点,是否比父节点大,如果子节点比父节点大,就把他们的值交换。再以子节点为父节点,找新的子节点,再调整。
完整代码
// 堆排序 // 建大根堆,先找最大的数,再把最大的数放到最后一位,然后n--,再向下调整
void AdjustDwon(int* a, int n, int root)
{
int parent = root;
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] > a[child])
child++;
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
void HeapSort(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDwon(a, n, i);
}
while (n--)
{
Swap(&a[0], &a[n]);
AdjustDwon(a, n, 0);
}
}
冒泡排序BubbleSort
冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
// 冒泡排序
void BubbleSort(int* a, int n)
{
while (n)
{
for (int i = 0; i < n - 1; i++)
{
if (a[i] > a[i + 1])
Swap(&a[i], &a[i + 1]);
}
n--;
}
}
快速排序(快排)QuickSort
(都无法通过,卡在2222循环的数据了,也就是快排最怕遇到的情况,有序的,只有一个数的数据,不但大量消耗栈空间,处理数据的过程跟冒泡一样,甚至更麻烦)
选最右边的值做key,那么一定要让左边begin先走,这样能保证他们相遇的位置是一个比key大的位置;选最左边的值做key,同理要让end先走。
啊哈算法里面的那个,快排思想。那里的基准数是现在的key。
反正都是在头或尾选基准数key,然后从另一头开始找值。意思就是key选左边,就从右边开始找值。key在右边,就从左边开始找值。
快速排序的特性总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN) // 递归的深度
- 稳定性:不稳定
缺陷
数列不能是接近有序的,否则时间复杂度是O(N2)。而且会导致栈溢出。因为是递归吗~
三数取中法,规避缺陷情况
防止取key的时候取到最大值或最小值。所以找数组的中位数和最左边和最右边三个数进行比较。选这三个数中间的那个。既不选最小也不选最大。保证排完序之后,div不在两端即可。当然选出来中位数之后,把它和key交换位置。就能避免缺陷了。避免缺陷后,这个排序就是无敌的O(N*logN)了。好吧,也不是无敌的,对于只有一个数的数列,再怎么找也找不到合适的基准数。
int midnomber(int a, int b, int c)
{
if (a > b)
{
if (b > c)
{
return b;
}
if(c > a)
{
return a;
}
return c;
}
else
{
if (c > b)
{
return b;
}
if (c < a)
{
return a;
}
return c;
}
}
就是找三个数的中间数的函数。
但是正常情况下,三数取中法可以规避掉这个区间的最大值或者最小值,选合适的数作基准数。
快排的实现方式
双(左右)指针法
两个指针begin和end。begin从数组的头开始向后找数,end从数组的尾开始向前找数。当begin遇到比基准数(key)大的就停止,否则就++begin(继续向后找);而end从当前数组的尾开始倒着找比基准数小的数,当end指向的数符合条件,进行交换,把begin和end指向的数交换位置。较大的数就移动到数组后面去,较小的数就排到数组前面了。
// 双指针法
int midnomber(int a, int b, int c)
{
if (a > b)
{
if (b > c)
{
return b;
}
if(c > a)
{
return a;
}
return c;
}
else
{
if (c > b)
{
return b;
}
if (c < a)
{
return a;
}
return c;
}
}
void QuickSort(int* a, int left, int right)
{
if (left >= right) return;
int midd = midnomber(left, (left + right) / 2, right);
Swap(&a[left], &a[midd]);
int key = left;
int begin = left;
int end = right;
while (begin < end)
{
while (begin < end && a[end] >= a[key])
{
end--;
}
while (begin < end && a[begin] <= a[key])
{
begin++;
}
Swap(&a[begin], &a[end]);
}
Swap(&a[key], &a[begin]);
QuickSort(a, left, begin - 1);
QuickSort(a, begin + 1, right);
}
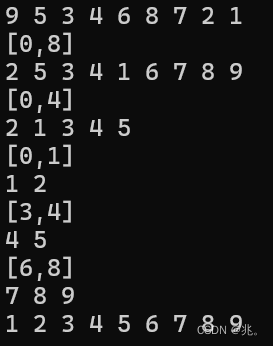
递归,分治法,也就是大事化小,小事化了的方式。把[0,8]分成[0,4]和[6,8]。再划分[0,1]和[3,4],对于一个数的区间直接忽略,一个数既是最大也是最小,排不了。
在第一次处理数据的时候,针对的是[0,8]这个区间,不难发现,利用三数取中法,我们取6作为基准数,在第一次排好数组中,6的左边都比6小,右边都比6大。
挖坑法
假设基准数都是最左边的那个。
先把基准数那里的数取出来(保存到key),相当于数组的最左边就为空了,也就是挖了一个坑,然后再从最右边往左找比key小的数。同时把这个小的数移到前面那个坑里面去。(虽然数组里面的数并没有真正消失,变成那个坑。但是在某种意义上它就是坑。)。接着再从左往右找比基准数大的数移到那个坑里去。当这两个指针相遇的时候,就把key基准数填进去。
其实和双指针法差不多。
void QuickSortKeng(int* a, int left, int right)
{
if (left >= right) return;
int midd = midnomber(left, (left + right) / 2, right);
Swap(&a[left], &a[midd]);
int key = a[left];
int begin = left;
int end = right;
while (begin < end)
{
while (begin < end && a[end] >= key)
{
end--;
}
a[begin] = a[end];
while (begin < end && a[begin] <= key)
{
begin++;
}
a[end] = a[begin];
}
a[begin] = key;
QuickSortKeng(a, left, begin - 1);
QuickSortKeng(a, begin+1,right);
}
最好也加上三数取中法
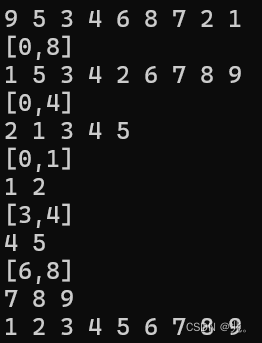
对于挖坑法,原理和前后指针法差不多,不过前后指针法,需要先找到符合条件的两个数,才能完成交换。而挖坑法是一直保持一个坑用来存放数据。在第一次[0,8]这个区间,也是先用三数取中法以6为基准数,把小于6的放左边,大于6的放右边。最后一个坑放基准数。
前后指针法
创建两个指针prev和cur。cur负责遍历数组,prev负责记录比基准数小的数的最右边的下标。
假设基准数是数组最右边的数。
那么cur和prev就从左边开始向右遍历数组,cur从左到右依次遍历数组,prev也是从左到右遍历。定义prev比cur的起始位置靠左一位。
不同的是,cur的作用是识别当前指向的数的大小。如果cur所指的数小于基准数key,说明它的位置正确,cur和prev同时右移一次。
当cur指向的数大于基准数,prev指向这个数的下标。然后cur继续后移,寻找比基准数小的数。当cur向后移动的时候有两种结果:找到一个比基准数小的数,那么交换cur和prev所指向的数,把大的数后移,同时cur和prev右移一次;cur直到遍历完整个数组都没找到比基准数小的数,因为此时prev还指向比基准数大的数,最后再交换基准数和prev。
然后就是划分下次递归的区间。
// 前后指针法
void QuickSortp(int* a, int left, int right)
{
if (left >= right) return;
int midd = midnomber(left, (left + right) / 2, right);
Swap(&a[right], &a[midd]);
int key = a[right];
int cur = left;
int prev = cur;
while (cur < right)
{
if (a[cur] < key && a[prev] < key)
{
cur++;
prev++;
}
else if (a[cur] < key && a[prev] > key)
{
Swap(&a[prev], &a[cur]);
prev++;
cur++;
}
else
{
cur++;
}
}
Swap(&a[prev], &a[cur]);
QuickSortp(a, left, prev - 1);
QuickSortp(a, prev + 1, right);
}
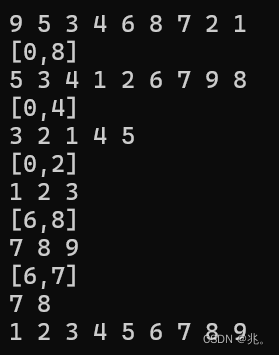
这三种快排排序的效果都不太一样,但是消耗的时间都差不多。
有人说,前后指针法里面的两个指针就像两个火车头,cur在前面移动,prev把符合条件的车厢链接到自己这边,prev遇到不符合条件的车厢就等cur找合适的车厢。
快排的非递归方式
因为快排是递归类型的,在使用递归的时候会大量消耗栈空间。所以为了优化这种情况,面试官会要求用非递归的方式,实现快排。
非递归的方式,就是建立一个栈,这个栈来储存每次递归的区间。当栈清空的时候说明所有数据都被排好序了。
整体思路:
建立一个while循环,循环的条件就是栈里有数据,用StackEmpty来判断栈的情况.当然没学c++呢,只能是用手搓的c语言的栈。还要再导入文件到项目里面,这里就先不实现了。
在进入while循环之前把整个数组的左右下标入栈。然后进入循环。
循环:先从栈里面获取数组的下标,然后调用一次快排,这个快排的返回值是中间值。然后是入栈操作,如果像先处理左区间,就先入右区间。因为栈是后进先出。在入栈的时候,要分情况,可以是建立一个结构体,这个结构体就是存区间的下标。或者不创建结构体,直接把区间的下标存进去。这时候还要分情况,是先入区间的左下标还是右下标。因为取的时候是反过来的。
循环的大概流程:判断栈是否为空,不为空就取数据,进行快排得到中间值下标,再入数据进栈。当栈为空就退出
// 伪代码
int QuickSortPart(int*a,int left,int right)
{
int midd = midnomber(left, (left + right) / 2, right); // 三数取中
Swap(&a[left], &a[midd]);
int key = left;
int begin = left;
int end = right;
while (begin < end)
{
while (begin < end && a[end] >= a[key])
{
end--;
}
while (begin < end && a[begin] <= a[key])
{
begin++;
}
Swap(&a[begin], &a[end]);
}
Swap(&a[key], &a[begin]);
return begin;
}
void QuickSort(int* a, int left, int right)
{
// 建立一个栈
Stack st;
StackInit(&st);
StackPush(&st,right - 1); // 先入的右,就要先取左
StackPush(&st,left);
while(!StackEmpty(&st))
{
int begin = StackTop(&st); // 先取区间左下标
StackPop(&st);
int end = StackTop(&st);
StackPop(&st);
int div = QuickSortPart(a, begin, end);
if((div - 1) - left > 1)
{
StackPush(&st,div-1);
StackPush(&st,left);
}
if(right - (div + 1) > 1)
{
StackPush(&st,right);
StackPush(&st,div + 1);
}
}
}
归并排序(外排序)MergeSort (像后序遍历)(可过OJ)
上面的排序都叫内排序,指在内存中排序效果更好。
归并排序是外排序,使用在硬盘、文件排序。
归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。(文件与文件之间排序,可以极少的占用内存)
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
归并排序的内存中(内排序)实现方法
// 归并排序
void MergeSortPart(int* a,int left,int right,int* tmp)
{
if (left >= right) return;
// 把目前的数组分成左右两个区间
int begin1 = left, end1 = (left + right) / 2;
int begin2 = ((left + right) / 2) + 1, end2 = right;
MergeSortPart(a, begin1, end1, tmp); // 一直向左区间递归,直到左区间不可被划分
MergeSortPart(a, begin2, end2, tmp); // 如果左区间到头了,返回后才是这个递归的开始
int i = 0; // 作为两个区间比较后插入到tmp数组的位置
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[left+i] = a[begin1];
begin1++;
}
else
{
tmp[left+i] = a[begin2];
begin2++;
}
i++;
}
while (begin1 <= end1) // 如果左区间还有剩余的数,再移到tmp数组中
{
tmp[left+i] = a[begin1++];
i++;
}
while (begin2 <= end2) // 这里是检查右区间
{
tmp[left+i] = a[begin2++];
i++;
}
for (int i = left; i <= right; i++)
{
a[i] = tmp[i]; // 再把tmp空间的数据移到原数组
}
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n); // 临时空间来暂存数据
MergeSortPart(a, 0, n - 1, tmp);
free(tmp); // 排完序后原数组有序,临时空间就没用了
}
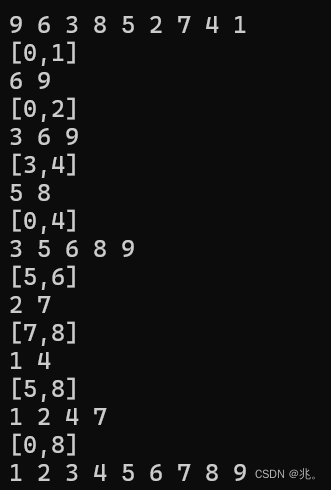
不难发现,本应是[0,8]的数组被划分成小份小份的。也就是先一直划分到左区间不可被划分的状态才停止,即[0.1]。然后逐层上返至[0,2]等等。
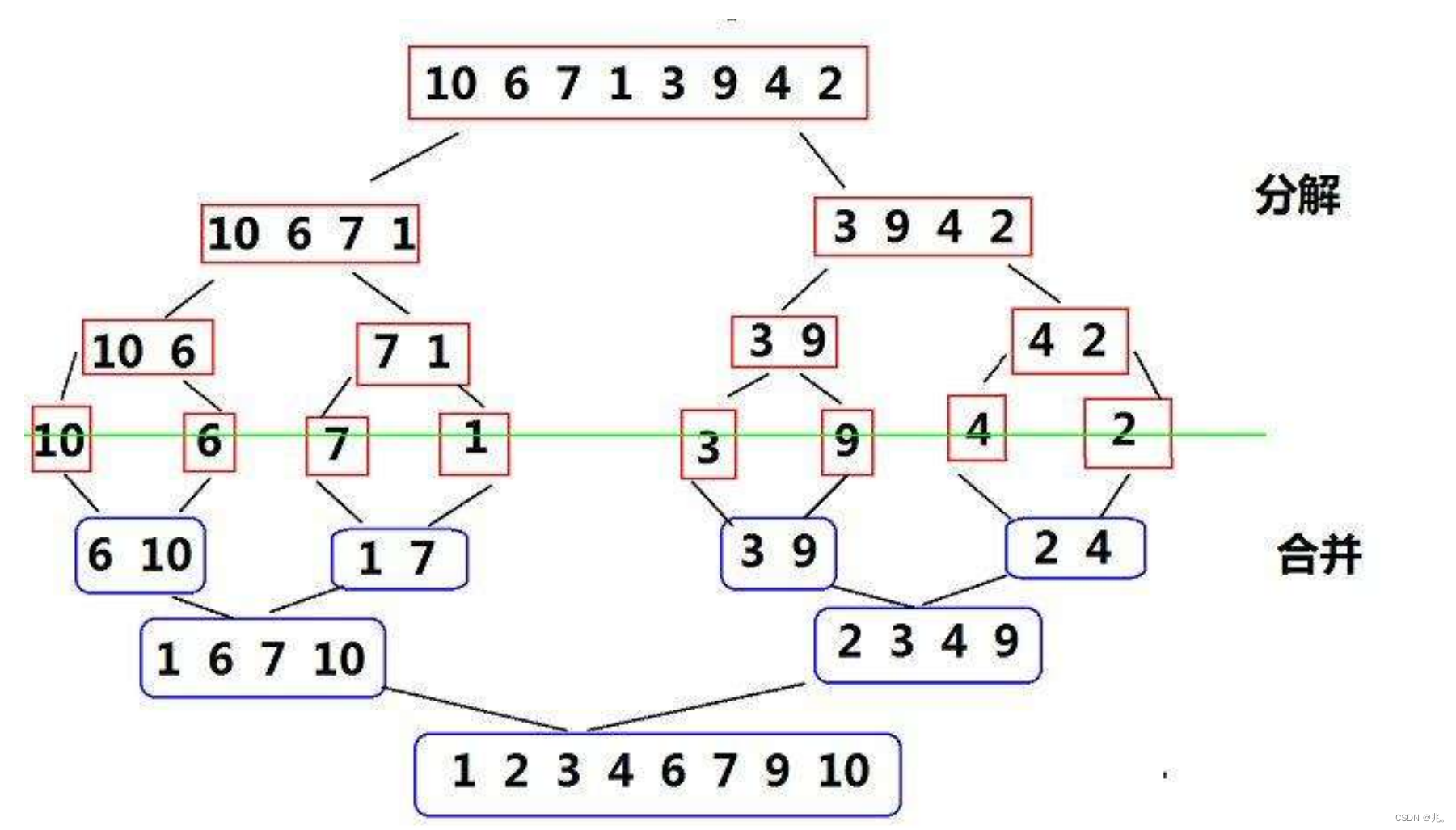
大概的过程就是这样。
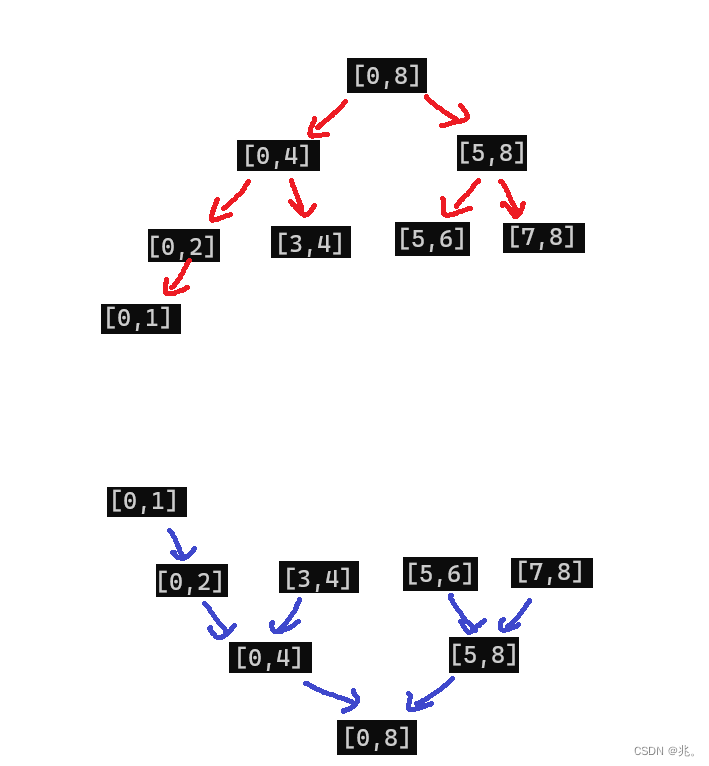
就像二叉树的后序遍历一样,不过这里先是把区间划到最小的可以排序的区间[0,1],也就是开始往回返的开始,也是处理数据的开始。从这一步,排序才开始。
归并排序内排序的非递归
跟快排递归改非递归的方法一样,都是把区间入栈,再从栈中取数据出来处理。等学了c++再实现。
好吧,还是有必要记一下,因为除了用栈,还有另一种方法实现归并排序的非递归。
要先理清一个思路,在递归的时候,第一次数据处理发生的时候,是在小区间,也就是数据两两一组。还有归并排序的特性,即把两组有序的数据合并。
所以,我们从最小的区间开始合并数组。也就是[0,1] [2,3] ;[4,5] [6,7] ;[8,9].
很明显,我们也可能会遇到奇数的i情况,因此还要修正区间的右下标。
因为是两个区间进行合并,防止一个区间被多次合并,我们还要一个特殊的变量。比如,01和23会合并一次.我们希望下次处理的数据是45和67。在0与4之间隔的是2*gap个数据。这里的gap就是每个区间数据的多少。gap从2开始。每次循环gap都要乘2.当gap大于总数据n的时候结束。
下一次再处理数据的时候,这个区间要变成之前的二倍,2gap=4,[0,1,2,3] [4,5,6,7]; [8,9].。
对于后面89这个区间的数据,它不满足2gap个数据。所以要及时修正一下区间的大小。
归并排序的外排序实现方法(加餐)
这是道面试题:给你10亿个数的文件,正常来说绝大多数的排序都是内排序,也就是需要把数据移到内存中,再排序。很明显,10亿个数比较庞大,无法一次性放到内存中去。所以我们可以把这个十分庞大的数据分割成小份的,具体是多小呢?要看你所使用的电脑最大能在内存中处理的数据。如果你的电脑最大可以一次性排100万位数,那就把10亿个数切成1000份小文件。再切这些小文件的时候,进行小范围的排序。保证每个文件里面的数据是拍好序的,可以用快排排序。然后写到文件里面。完成切割之后。
再用归并排序的外排序,可以是把相邻两个文件排序放到新文件,再把两个新文件合并。一直到最后一个。
void MergeSortFile()
{
// 打开大文件
// 读取大文件的前100万个数据,放到内存中排序,再写到子文件1中。
// 一直到大文件全部分割完毕
// 再把子文件1和2合并到12.3和4合并到34……
// 因为每个子文件都是有序的,所以可以用归并排序进行外排序
}
比较的困难的是给子文件取名,还有子文件合并的时候,子文件名称的获取
但是据说c++也有专门的库,先不实现了,把思路写一下。。。
一些小众的排序
计数排序
就是类似之前学的桶排序(虽然不是真正意义上的桶排序),但是这个排序在某些条件下也很快。
条件:数量足够大且特别集中。
意思就是给你一堆数,这些数都在一个比较小的范围里面,这个范围就是最大的数减去最小的数的差值rang。
然后去遍历这些数,把最小的数放在0的位置,最大的数放在rang的位置。
遍历的时候,让得到的数减去最小数,再放到新数组里面去,这个新数组就是统计每个数出现的次数。
遍历完原数组之后,再逆向写到原数组里面,不过这次就是按顺序写进去了。(写到原数组的时候再把最小值加上,复原)
如果原数组是N个数
那么时间复杂度就是O(MAX(N,rang)) (N和rang较大的那个)
空间复杂度是O(rang)
基数排序
但是真正的桶排序是按照位数的大小分类的,比如是三位数,放进一个桶,两位数就放另外一个桶。
排序算法复杂度及稳定性分析
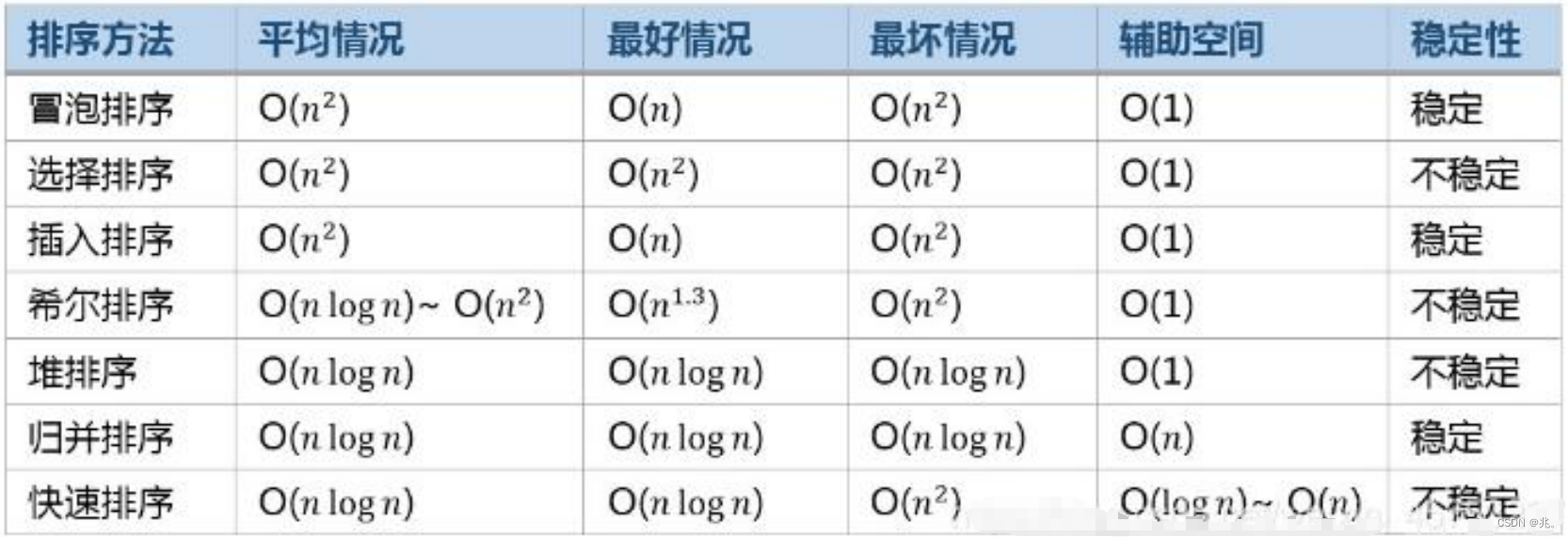
这个表格不要背,要理解。
关于稳定性的理解
数组中相同值,排完序相对顺序可以做到不变就是稳定的否则就不稳定
递归的缺陷
因为递归是在栈上进行的,递归可以以大化小。但是递归再继续往小里划分的时候,栈上堆积的函数栈帧太多了。会爆掉,所以,还可以在函数里面加一个条件,当这个区间不到10个数的时候,就把这个区间交给直接排序。
递归改非递归的方式
- 把递归的过程改成循环,比如斐波那契数列求解,当然也仅限于比较简单的递归过程。
- 用栈模拟数据存储
递归改非递归为什么
- 提高效率 因为递归建立栈帧是有消耗的,虽然现代计算机,已经可以忽略这个问题了
- 因为递归是需要建立函数栈帧的,消耗的是栈空间,而且对于系统而言,栈空间都是M级的,也就是按MB来算的;对于非递归来说,数据存储在堆上,堆的空间是G级的,也就是GB。相比之下,还是堆上储存更好。
测试排序的接口
// 排序实现的接口
// 插入排序
void InsertSort(int* a, int n);
// 希尔排序
void ShellSort(int* a, int n);
// 选择排序
void SelectSort(int* a, int n);
// 堆排序
void AdjustDwon(int* a, int n, int root);
void HeapSort(int* a, int n);
// 冒泡排序
void BubbleSort(int* a, int n);
// 快速排序
void QuickSort(int* a, int left, int right);
// 归并排序
void MergeSort(int* a, int n);
// 测试排序的性能对比
void TestOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int)*N);
int* a2 = (int*)malloc(sizeof(int)*N);
int* a3 = (int*)malloc(sizeof(int)*N);
int* a4 = (int*)malloc(sizeof(int)*N);
int* a5 = (int*)malloc(sizeof(int)*N);
int* a6 = (int*)malloc(sizeof(int)*N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
}
int begin1 = clock();// 获取程序运行此处的时间,单位:毫秒 // 头文件<time.h>
InsertSort(a1, N);
int end1 = clock(); // 时间之差就是该排序函数所用时间
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort(a5, 0, N-1);
int end5 = clock();
int begin6 = clock();
MergeSort(a6, N);
int end6 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("QuickSort:%d\n", end5 - begin5);
printf("MergeSort:%d\n", end6 - begin6);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
}
测试排序算法的OJ题
https://leetcode-cn.com/problems/sort-an-array/
一些练习题
- 快速排序算法是基于( )的一个排序算法。
A分治法
B贪心法
C递归法
D动态规划法
2.对记录(54,38,96,23,15,72,60,45,83)进行从小到大的直接插入排序时,当把第8个记录45
插入到有序表时,为找到插入位置需比较( )次?(采用从后往前比较)
A 3
B 4
C 5
D 6
3.以下排序方式中占用O(n)辅助存储空间的是
A 简单排序
B 快速排序
C 堆排序
D 归并排序
4.下列排序算法中稳定且时间复杂度为O(n2)的是( )
A 快速排序
B 冒泡排序
C 直接选择排序
D 归并排序
5.关于排序,下面说法不正确的是
A 快排时间复杂度为O(N*logN),空间复杂度为O(logN)
B 归并排序是一种稳定的排序,堆排序和快排均不稳定
C 序列基本有序时,快排退化成冒泡排序,直接插入排序最快
D 归并排序空间复杂度为O(N), 堆排序空间复杂度的为O(logN)
6.下列排序法中,最坏情况下时间复杂度最小的是( )
A 堆排序
B 快速排序
C 希尔排序
D 冒泡排序
7.设一组初始记录关键字序列为(65,56,72,99,86,25,34,66),则以第一个关键字65为基准而得到
的一趟快速排序结果是()
A 34,56,25,65,86,99,72,66
B 25,34,56,65,99,86,72,66
C 34,56,25,65,66,99,86,72
D 34,56,25,65,99,86,72,66
答案:
1.A 2.C 3.D 4.B 5.D 6.A 7.A




![[dataworks]从mysql导入数据](https://img-blog.csdnimg.cn/direct/49c640a986da4e83b307655dbff82f03.png)