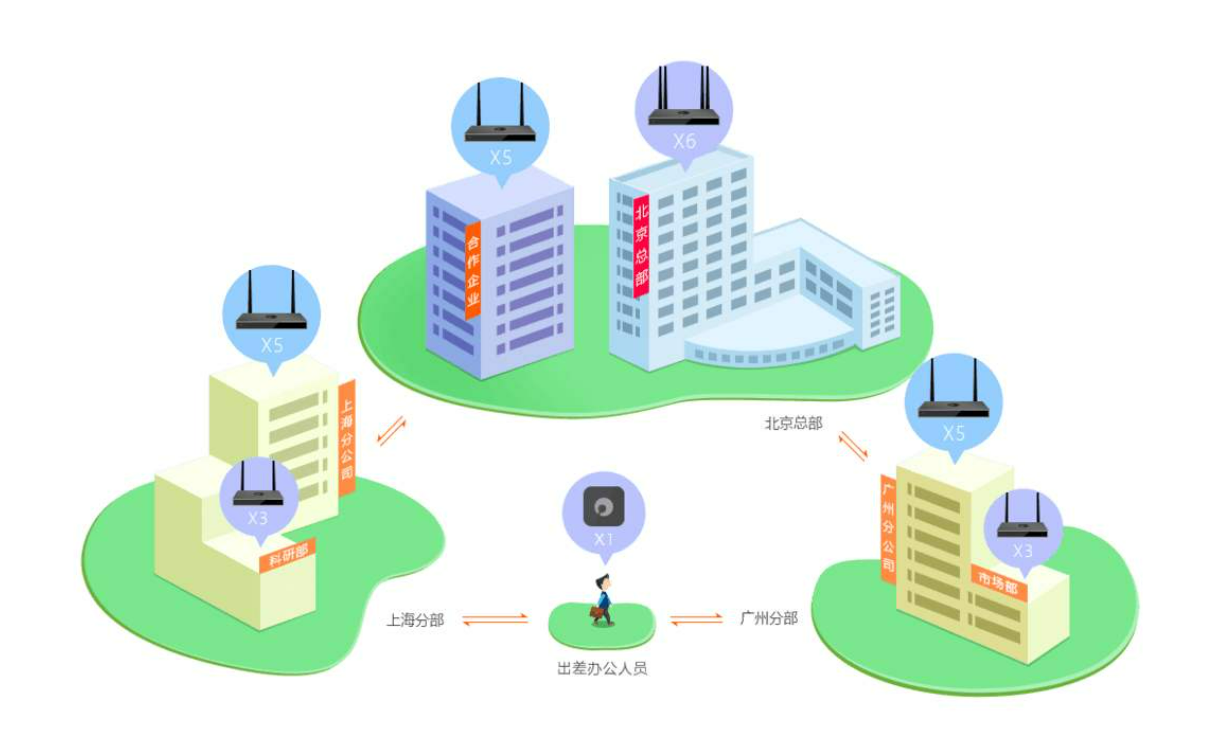
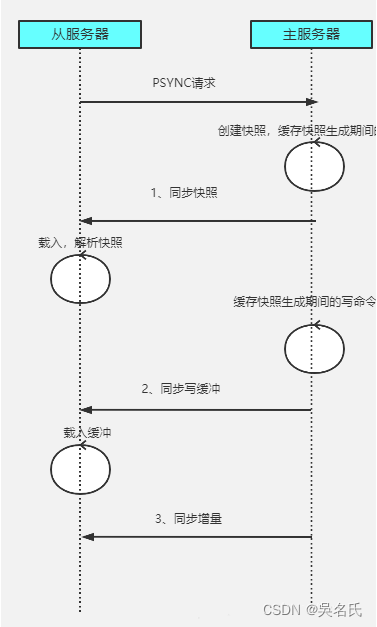
想上蓝名，赛前1414分，目标蓝名。
$update$赛后排名$57$。

A. Polycarp and the Day of Pi
题意 给你一个数字判断该数字是否和圆周率的前30位匹配。
思路 发现样例有一个长度为30为的数，$ctrl+cv$一下，暴力判断即可。
代码

B. Taisia and Dice
题意 给你$n$个骰子，当前$n$个骰子的总得分为$s$，去掉一个分数最大的骰子得分为$t$，构造这$n$的骰子的得分，得分<= 6 , $n<=50$。
思路 容易发现最大值为$s$ - $t$,现判断所有骰子都为最大得分能否组成$s$，再暴力一层一层的把得分分配给剩下的$n-1$个骰子。
代码

C. Premutation
题意 给你一个排列数组$p$,然后给你$n$个数组，每个数组分别为排列$p$去掉第$i$项$p_i$后的数组，通过这$n$个数组反推排列数组$p$，$(3\le n\le 100)$,去掉的项的下标不保证有序，但保证是个排列。

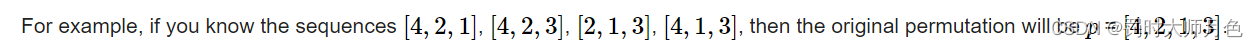
思路 统计每个值在$n$个数组出现的下标和，排序即可。
代码

D. Matryoshkas
题意 给你一个数组$a_i$,我们把连续序列成为该序列是连续的数字组成，问你这个数组能由多少个连续序列组成，$n<=2e5$。
样例

6
2 2 3 4 3 1

2

样例解析：可以分解为$[1,2,3,4]$ , $[2,3]$。
思路 暴力模拟即可，从小到大枚举所有首项，并截取下来最长的连续序列，统计个数即可。
代码

E. Vlad and a Pair of Numbers
题意 问你是否存在两个数，给定一个$x$,满足$x==(a+b)/2==(a$^$b)$ , 不是下取整，是整除2 , 取值范围$a、b<=2^2$${}^9$。
思路 赛时考虑$(a+b)/2==(a$ ^ $b)$这个式子什么时候成立，考虑第$k$位，如果第$k$位为1，我们发现只有一个为1才能保证异或为1，要满足$(a+b)/2$为1，加号再除以2需要两个1才能保证第$k$位位1，那我们如何去构造一个1呢，我们可以考虑借低位的1去构造一个高位的1，这就要求低位不能为0，并且低位只能为两个1，然后构造出来了一个高位的1，第$k$位 为0，默认看成都为0即可 。
代码

做到$e$只用了半小时，$A-E$是比较偏$edu$的简单题，绝大部分小白能够做出$d,e$部分，能力较强的可以在$div3$只做出前五道就可以拿到不错的名次，是一个很好的上分场。

F. Timofey and Black-White Tree
题意 给你一个大小为$n$的树，最开始$c0$点为黑色，然后执行$m$次操作，每次操作把一个点染成黑色，每次染色后问你所有黑色点对之间的最小距离。
思路 赛时用了一个树剖+线段树的方法去做的，思路是考虑维护两种关系一个是加了这个点，答案在这个新加的点到这个点所在子树的黑点的之间的最短距离，用dfs维护线段树维护。第二个是考虑不在这个子树的影响，答案肯定是$d[u]+d[v]-2\ast d[lca(u,v)]$，我们维护后面的$d[v]-2\ast d[lca(u,v)]$,我们发现$lca(u,v)$一定是$u$的祖先，我们考虑维护$v$节点到根的路径所有的$d[v]-2d[t]$的最大值，$t$是$v$的祖先，然后$u$,$v$的$lca$一定是两条到根路径的最大深度的交集。
赛后知道有一个更简单的$nsqrt(n)$的做法，是一个$dfs$的非常有用的暴力，该做法在后续中更新。
代码

今天的div3 的 F是个人类妙妙题，爆杀了我这种没脑子的蒟蒻。

$Updating$