红黑树插入数据的底层详解

红黑树定义

1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的，则它的两个孩子结点是黑色的
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色节点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

红黑树节点实现

enum COLOR {
	RED,
	BLACK
};

template<class K,class V>
struct ListNode {				// 节点
	//typedef ListNode<K, V> node;
	using Node = ListNode<K, V>;
	ListNode(std::pair<K,V> kv):_kv(kv) {
		_parent = _left = _right = nullptr;
		_color = RED;
	}
	Node* _parent;
	Node* _left;
	Node* _right;
	std::pair<K, V> _kv;
	COLOR _color;
};

简单点来说就是一个结构体,里面三个指针,一个pair<k,v>数据,一个颜色(enum变量),三个指针是父亲,左孩子,右孩子

依照二叉搜索树的定义,我们来实现插入操作

1.接口

这里我按stl库里set,map的insert函数最主要的模型进行实现

2.找到待插入的位置

按搜索二叉树的要求,比根节点大的去右子树,比根节点小的去左子树,如果和根节点相等则插入失败,否则在子树继续比较,直到找到叶节点,

Node* new_node = new Node(kv);
_size++;
if (_root == nullptr) {
	new_node->_color = BLACK;
	_root = new_node;
	return std::make_pair(iterator(new_node), true);
}
Node* child = _root;
Node* father = _root;	// 父子交替,找 新节点应该插入的地方
while (child) {			//儿子不是空
	father = child;
	if (child->_kv.first > kv.first) {
		child = child->_left;
	}
	else if (kv.first > child->_kv.first) {
		child = child->_right;
	}
	else {
		
		_size--;
		return std::make_pair(iterator(child), false);
	}
}

3.插入新节点

		void add_node(Node* father, Node* new_node) {
			if (new_node->_kv.first > father->_kv.first) {
				father->_right = new_node;
			}
			else {
				father->_left = new_node;
			}
			new_node->_parent = father;
		}

插入完成,依照红黑树的定义对原树进行重构

把红黑树的定义拉过来

1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的，则它的两个孩子结点是黑色的
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色节点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

默认新节点的颜色为什么是红色

如果新节点是黑色,新插入节点所在路径上的颜色一定不同于其他路径.定义4失效,此时需要更改某些路径上的黑色节点,最差情况需要重构整颗树

如果新节点是红色,如果父亲节点是红色的话定义三失效,此时需要对所在子树进行选择,最差情况也不过是选择一条逻辑,如果插入的是根节点,也会违反定义5,此时只需直接修改颜色即可

对比之下,新节点为红色时,重构树的代价最小,

重构

情况一,没有父节点

此时插入的节点只可能是根节点,直接修改颜色

情况二,父亲节点为黑色

此时不与红黑树冲突,不需要重构

情况三,父亲节点为红色

父亲为红色,由于性质三的限制,爷爷节点不能为红色,必定为黑色

此时需要注意叔叔节点的颜色

情况三_一.没有叔叔节点

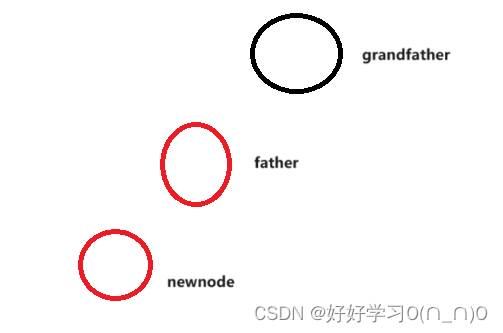
这种情况不能单靠修改颜色来重构树,需要进行旋转

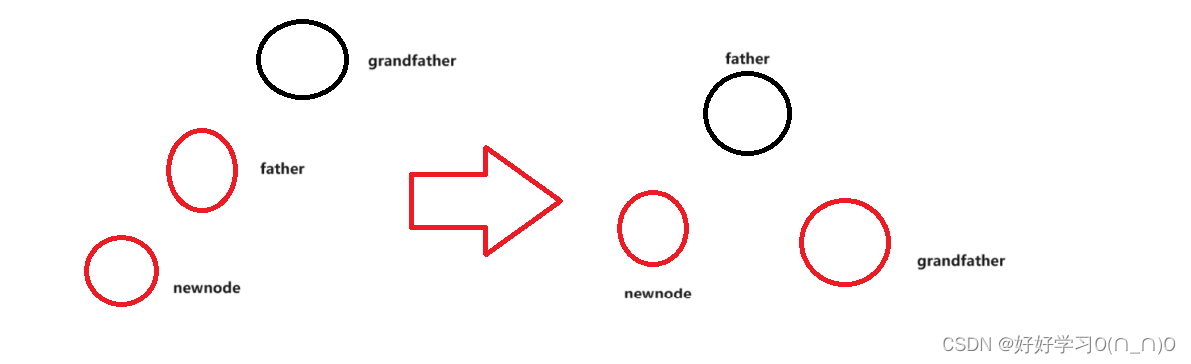
关于父子所在不同位置进行不同的旋转可以参考AVL树底层原理+模拟实现-CSDN博客

简单来说:

父亲为爷爷左,孩子为父亲左,则右旋父亲
父亲为爷爷右,孩子为父亲右,则左旋父亲
父亲为爷爷左,孩子为父亲右,则先左旋孩子,再右旋孩子
父亲为爷爷右,孩子为父亲左,则先右旋孩子,再左旋孩子

关于颜色

如果父亲孩子同侧父亲 -> 黑色爷爷 -> 红色如果父亲孩子异侧新节点 -> 黑色爷爷 -> 红色

			if (uncle == nullptr ) {							// 叔叔为空,需要发生旋转
				Node* tmp = revorve(new_node, parent, grandparent);
				if (tmp == _root) {
					tmp->_color = BLACK;
				}
				else {
					reconstitution(tmp);
				}
			}

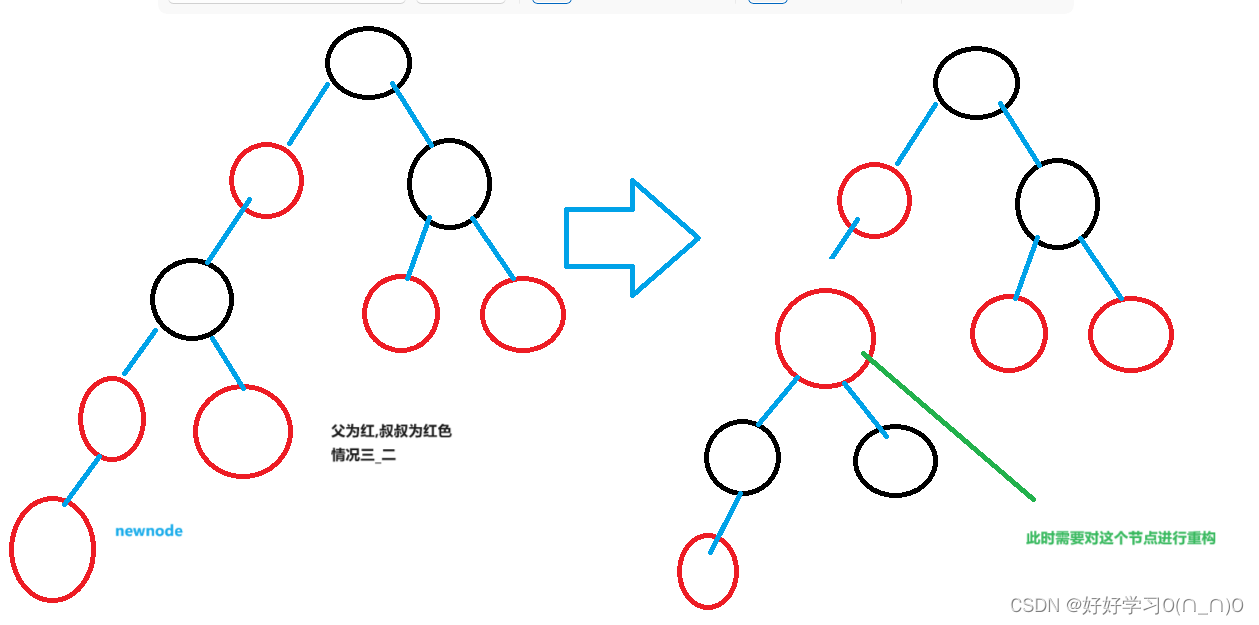
情况三_二.叔叔节点为红色

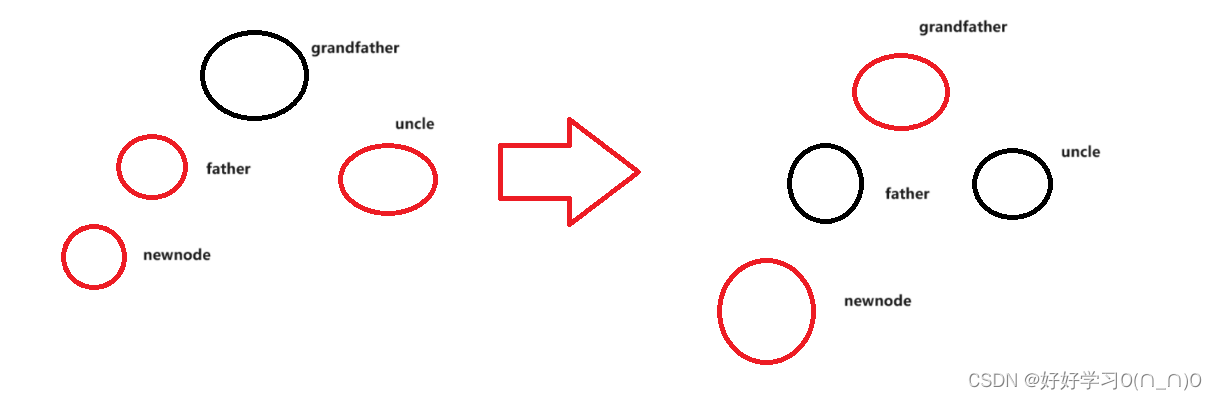
这种情况可以靠修改颜色来完成重构,但是需要注意,此时爷爷节点被强制修改为了黑色,此时就需要再对爷爷节点进行重构

else if (uncle->_color == RED) {
	// 叔叔为红色 需要改变颜色,并继续向上重构,因为新的爷爷节点被强制改为红色,需要继续向上重构
	uncle->_color = parent->_color = BLACK;
	if (grandparent != _root) {
		// 爷爷节点不为root的话
		grandparent->_color = RED;
		reconstitution(grandparent);
	}
}

情况三_三叔叔节点为黑色

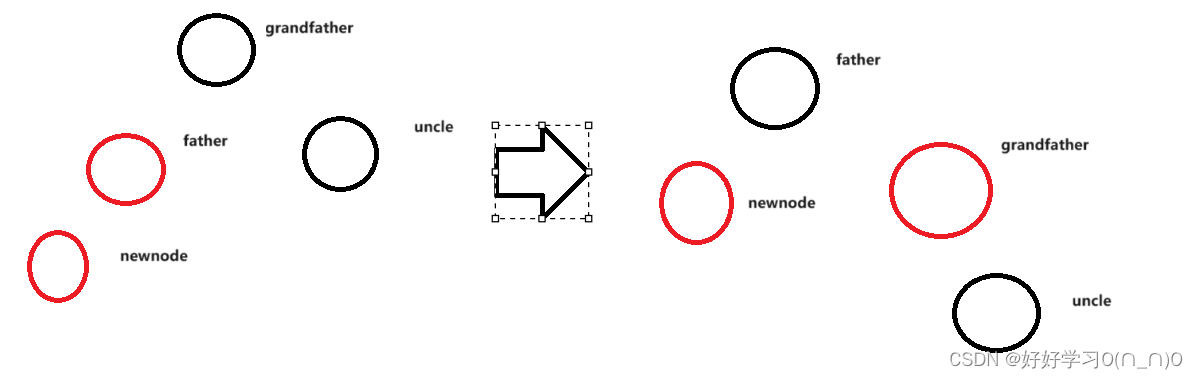
这种情况需要先将新节点与父节点旋转为同侧，再旋转新的父节点，与爷爷的颜色互换(这张图只是为了便于观看理解过程!)

if (uncle->_color == BLACK) {							// 叔叔为空,需要发生旋转
	Node* tmp = revorve(new_node, parent, grandparent);
	if (tmp == _root) {
		tmp->_color = BLACK;
	}
	else {
		reconstitution(tmp);
	}
}

附：为什么会出现情况三_三

依照红黑树的定义四:每条路径上的黑色元素数量相等,显然下图中的红黑树本身就已经不合定义了,那么为什么还会出现这种情况呢?

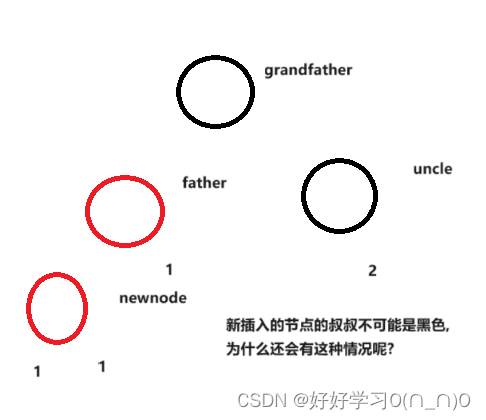
在情况三_三中如果我们假设被重构的节点是新加入的节点的话,显然是不符合定义的,但是,除了是新加入的节点以外,还有一种情况,就是情况三_二中继续向上重构的节点.

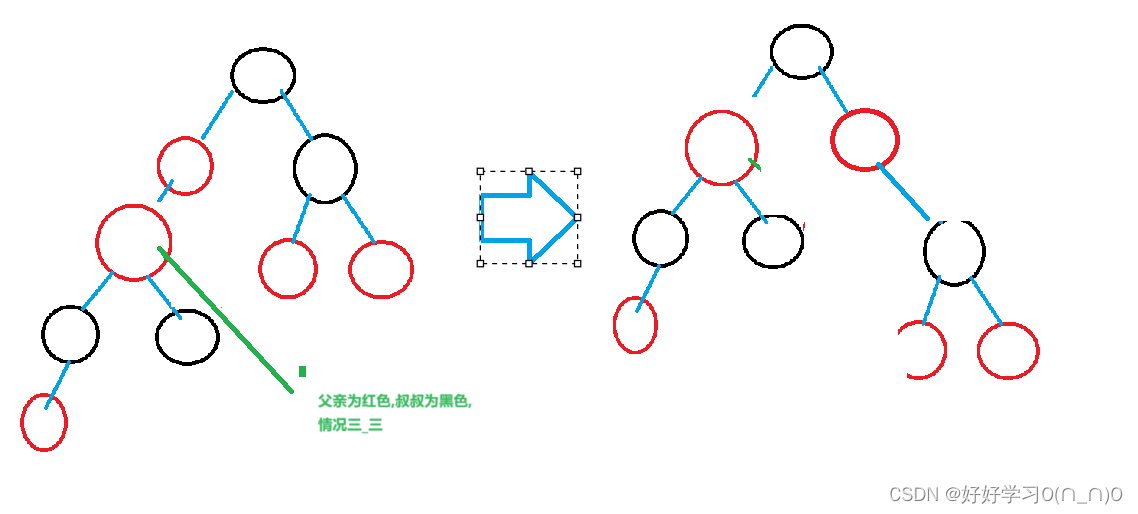
这种递归式的重构就会出现情况三_三了

总结

插入节点为根节点,进行重构 ------ 修改根节点颜色为黑色
父亲为红色,没有叔叔节点进行重构 ------- 将父节点与子节点旋转至同侧，旋转父节点。如果父亲孩子同侧父亲 -> 黑色爷爷 -> 红色如果父亲孩子异侧新节点 -> 黑色爷爷 -> 红色
父亲为红色，叔叔节点为红色 -------- 父亲与叔叔节点修改为黑色，爷爷节点修改为红色，继续重构爷爷节点
父亲为红色，叔叔节点为黑色 -------- 将父节点与子节点旋转至同侧，旋转父节点。如果父亲孩子同侧父亲 -> 黑色爷爷 -> 红色如果父亲孩子异侧新节点 -> 黑色爷爷 -> 红色

模拟实现参考代码

		std::pair<iterator,bool> insert(const std::pair<K, V>& kv) {
			Node* new_node = new Node(kv);
			_size++;
			if (_root == nullptr) {
				new_node->_color = BLACK;
				_root = new_node;
				return std::make_pair(iterator(new_node), true);
			}
			Node* child = _root;
			Node* father = _root;	// 父子交替,找 新节点应该插入的地方
			while (child) {			//儿子不是空
				father = child;
				if (child->_kv.first > kv.first) {
					child = child->_left;
				}
				else if (kv.first > child->_kv.first) {
					child = child->_right;
				}
				else {
					
					_size--;
					return std::make_pair(iterator(child), false);
				}
			}
			//此处儿子是空,代表新节点应该插入的地方
			add_node(father, new_node);
			//对插入的节点进行检查,不合理的地方重构
			reconstitution(new_node);
			return std::make_pair(iterator(new_node), true);

		}
	protected:
		void add_node(Node* father, Node* new_node) {
			if (new_node->_kv.first > father->_kv.first) {
				father->_right = new_node;
			}
			else {
				father->_left = new_node;
			}
			new_node->_parent = father;
		}
		void reconstitution(Node* new_node) {
			/*
			1. 每个结点不是红色就是黑色 
			2. 根节点是黑色的  
			3. 如果一个节点是红色的，则它的两个孩子结点是黑色的  
			4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均 包含相同数目的黑色结点  
			5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
			*/
			if (new_node == _root) {
				return;
			}
			if (new_node->_parent->_color == BLACK)	
				// 父亲是黑色,插入红色节点,符合红黑树要求,不做处理
				return;
			// 父亲是红色,此时不符合条件三,需要发生重构
			Node* parent = new_node->_parent;				// 新节点的父节点
			Node* grandparent = new_node->_parent->_parent; // 爷爷节点
			Node* uncle = nullptr;							// 叔叔节点
			if (grandparent->_left == parent) {				// 叔叔节点需要通过父亲节点与爷爷节点的关系来判断
				uncle = grandparent->_right;			
			}
			else {
				uncle = grandparent->_left;
			}
			

			// 判断情况
			if (uncle == nullptr || uncle->_color == BLACK) {							// 叔叔为空,需要发生旋转
				Node* tmp = revorve(new_node, parent, grandparent);
				if (tmp == _root) {
					tmp->_color = BLACK;
				}
				else {
					reconstitution(tmp);
				}
			}
			else if (uncle->_color == RED) {
				// 叔叔为红色 需要改变颜色,并继续向上重构,因为新的爷爷节点被强制改为红色,需要继续向上重构
				uncle->_color = parent->_color = BLACK;
				if (grandparent != _root) {
					// 爷爷节点不为root的话
					grandparent->_color = RED;
					reconstitution(grandparent);
				}
			}
			//else {	// 叔叔节点为黑色
			//	// 旋转
			//	reconstitution(revorve(new_node, parent, grandparent));
			//}
		}
		Node* revorve(Node* node,Node* parent,Node* grandparnt) {
			if (node == parent->_left && parent == grandparnt->_left) {
				// 子为父左，父为爷左，右旋父
				revorveR(parent);
				node->_color = BLACK;
				return parent;
			}
			else if(node == parent->_left && parent == grandparnt->_right) {
				// 子为父左，父为爷右，右旋子，左旋子
				revorveR(node);
				revorveL(node);
				parent->_color = BLACK;
				return node;
			}
			else if (node == parent->_right && parent == grandparnt->_right) {
				// 子为父右，父为爷右，左旋父
				revorveL(parent);
				node->_color = BLACK;
				return parent;

			}
			else {
				// 子为父右，父为爷左，左旋子，右旋子
				revorveL(node);
				revorveR(node);
				parent->_color = BLACK;
				return node;

			}
		}
		void revorveL(Node* node)
		{
			// 左旋需要改变node节点的 1.本身 2.父节点 3.爷爷节点 4.左孩子节点 共计四个节点
			// 记录四个节点的值，防止等下修改时混乱
			Node* parent = node->_parent;
			Node* grandparent = parent->_parent;
			Node* leftchild = node->_left;
			// 1.修改本身节点
			node->_parent = grandparent;
			node->_left = parent;

			// 2.修改父节点
			parent->_parent = node;
			parent->_right = leftchild;
			if (parent == _root)
				_root = node;

			// 3. 修改爷爷节点
			if (grandparent != nullptr) {
				if (grandparent->_left == parent)
					grandparent->_left = node;
				else {
					grandparent->_right = node;
				}
			}

			// 4. 修改左孩子节点
			if(leftchild != nullptr)
				leftchild->_parent = parent;
		}
		void revorveR(Node* node)
		{
			// 右旋需要改变node节点的 1.本身 2.父节点 3.爷爷节点 4.右孩子节点 共计四个节点
			// 记录四个节点的值，防止等下修改时混乱
			Node* parent = node->_parent;
			Node* grandparent = parent->_parent;
			Node* rightchild = node->_right;
			// 1.修改本身节点
			node->_parent = grandparent;
			node->_right = parent;

			// 2.修改父节点
			parent->_parent = node;
			parent->_left = rightchild;

			// 3. 修改爷爷节点
			if (grandparent != nullptr) {
				if (grandparent->_left == parent)
					grandparent->_left = node;
				else {
					grandparent->_right = node;
				}
			}

			// 4. 修改右孩子节点
			if(rightchild!=nullptr)
				rightchild->_parent = parent;
		}